Прямые методы построения функции принадлежности
Прямые методы для одного (уникального) эксперта состоят в непосредственном назначении степени принадлежности для исследуемых объектов хÎ Х или непосредственном назначении функции (правила), позволяющей вычислить значения mА(х).
Пример 3.1. Пусть возраст людей принимает значения из интервала Х=[0,100]. Понятие “молодой” можно интерпретировать как имя нечеткого множества А Í Х. Степень, с которой численное значение возраста, например, х = 27 совместимо с понятием “молодой”, будет 0,7, а, скажем для х равного 30 и 35 - соответственно 0,5 и 0,2. Функция mА”молодой” (х) может рассматриваться как функция принадлежности нечеткого множества А (“молодой”) со значением mА(х) в точке х, представляющим степень принадлежности понятию “молодой”. Т.е. функцию mА(х) можно построить путем аппроксимации по ряду степеней принадлежности на континууме Х.
Определенный интерес представляет метод семантических дифференциалов, предложенный К. Осгудом. Этот метод позволяет оценить принадлежность объекта, обладающего комплексом свойств (соответственно фокальные элементы и элементарные события). Метод заключается в следующем:
Определяется список свойств, по которым оценивается объект.
В списке находятся полярные свойства и формируются полярные шкалы.
Для каждой пары полюсов оценивается выделенное понятие на то, как сильно оно обладает выделенным свойством.
По совокупности оценок (в установленной шкале, например, от 0 до 1) определяется профиль понятия в виде вектора с координатами (изменяющимися от 0 до 1).
Полученный профиль рассматривается как нечеткое подмножество положительного списка свойств или шкал. Данный метод хорошо применим в задачах распознавания образов.
Пример 3.2. В задачах распознавания лиц можно выделить следующие шкалы:
| Список свойств | Полярные свойства (полюса) |
| х1- высота лба | <узкий - широкий>; |
| х2- профиль носа | <горбатый - курносый>; |
| х3- длина носа | <короткий - длинный>; |
| х4- разрез глаз | <узкие - широкие>; |
| х5- цвет глаз | <темные - светлые>; |
| х6- форма подбородка | <остроконечный - квадратный>; |
| х7- толщина губ | <тонкие - толстые>; |
| х8- цвет лица | <темное (смуглое) - светлое (бледное)>; |
| х9- очертание лица | <овальное - квадратное>. |
Светлое, квадратное лицо, у которого широкий лоб, курносый длинный нос, широкие, светлые глаза, квадратный подбородок, может быть определено как нечеткое множество {1/х1,...,1/х9} или вектор (111 111 111)Т. Лицо, соответствующее вектору (000 000 000)T - полярно противоположное.
Существует другой не менее удобный метод определения функции принадлежности объектов, сложному понятию А, например, удобный, комфортабельный и т.п. Этот метод ориентирован на вычисление частичной принадлежности друг другу строгих (четких) множеств. Суть этого метода такова. Имеется совокупность четких подмножеств Х1,...,Хm множества Х, таких, что Хi ¹ Æ и Х1È Х2È ...È Хm =Х. В крайнем случае, когда для любых i,j i¹j, Хi Ç Xj =Æ, имеет место четкое разбиение Х. В общем случае Хi Ç Xj ¹ Æ. Представим нечеткое множество А Í Х. Тогда
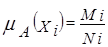 , ,
| (3.10) |
где Мi =ú Хi Ç Аjú - число элементов хÎ Х, относящихся к Хi и A одновременно;
Ni =ú ХiÈAú - число элементов в хÎ Х, относящихся или к Хi, или к A.
Пример 3.3. Пусть некий класс объектов обладает девятью возможными свойствами, т.е. Х = {х1, х2, х3,х4,х5,х6,х7,х8,х9}. Для простоты примем Х = {1, 2, 3, 4, 5, 6, 7, 8, 9}. Имеем пять объектов (фокальных элементов), обладающих соответствующими свойствами (элементарными событиями) {Х1, Х2, Х3, Х4, Х5,} = {{1, 3, 5}, {3, 6, 9}, {2, 4, 8}, {1, 3, 7}, {2, 3, 8}}. Понятие А, например, красивый, полезный, удобный и т.п. определено эталоном, включающим в себя следующий ряд свойств А={2, 3, 5, 8, 9}. Используя выражение 3.1, можно определить значение частичной принадлежности объектов Хi понятию А:
mА(Хi) = {1/3, 1/3, 1/3, 1/7, 3/5},
определяющее нечеткое подмножество
А = {1/3/X1, 1/3/X2, 1/3/X3, 1/7/X4, 3/5/X5} ,
показывающее, что наиболее соответствующее эталону, т.е. наиболее красивым, удобным, полезным и т.п. является Х5.
Рассмотренный метод имеет вероятностное толкование принадлежности фокальных элементов нечеткому множеству. Если множество Х конечно и число элементов (элементарных событий) этого множества равно n, то возможное число фокальных элементов Хi, состоящих из k элементарных событий (свойств, признаков, объектов), можно определить с помощью биномиального коэффициента 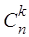 , а число возможных Хi при k =
, а число возможных Хi при k = 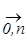 , как сумму
, как сумму 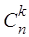 , т.е.
, т.е.
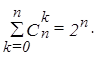
Получение степеней принадлежности через вероятности выбора элемента и отнесение его к определенному множеству наиболее отчетливо обосновано в методе уровневых множеств, представленном Р. Ягером.
Пусть задано нечеткое подмножество А множества Х. Рассмотрим случайный способ выбора элемента х из Х. Сначала случайным образом выбираем значения a Î [0,1], а затем также случайно - элемент из соответствующего множества a - уровня. Подсчитывается вероятность выбора конкретного элемента в условиях проводимого эксперимента.
Для простоты изложения предположим, что 0£ m1£m2£ ...£ mn , mn=mmax£1, где mi - степень принадлежности xi множеству А. Выпишем уровневые множества:
| при 0 < a £ m1 | Аa ={х1, х2, х3, ... , хn}= Х1, |
| при m1< a £ m2 | Аa ={ х2, х3, х4, ... , хn}=Х2, |
| при m2< a £ m3 | Аa ={ х3, х4, ... , хn}=Х3, |
| . . . . . . . . . . . . . . . | . . . . . . . . . . . . |
| при mn -2 < a £ mn -1 | Аa ={ х n-1, х n}= Х n-1, |
| при mn -1< a £ mn | Аa ={хn}= Хn, |
| при mn < a £ 1 | Аa = Æ . |
Поскольку в эксперименте значения a выбираются случайно, то вероятность того, что уровневое множество Хi окажется выбранным, равна
Р(Хi) = m i - m i-1. Кроме того, так как из выбранного множества элемент
выбирается случайно, то
| Р{выбрать элемент xi| Xj} | 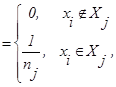
|
где nj - число элементов в Хi. Исходя из этого
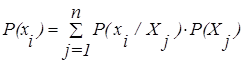 .
.
Из приведенных формул можно определить вероятность выбора элемента хi:
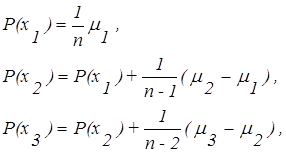
| (3.11) |
. . . . . . . . . . . . . . . .
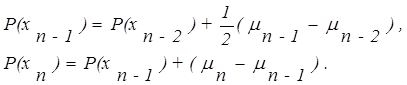 Р (выбранных элементов нет) =1 - mn.
Р (выбранных элементов нет) =1 - mn.
|
Заметим, что если i ³ j, то mi ³ mj и, следовательно, Рi ³ Рj. Разрешив систему (3.2) относительно Р(хi), можно убедиться, что сумма вероятности равна 1.
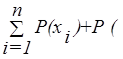 выбранных элементов нет выбранных элементов нет 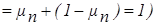 . .
|
Исходя из (3.2) можно выразить степени принадлежности mi через ве-
роятности Р(хi):
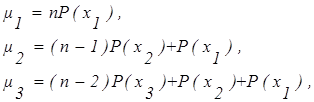
|
. . . . . . . . . . . . . . . . .
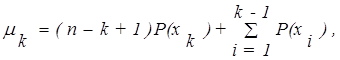
| (3.12) |
. . . . . . . . . . . . . . . . . .
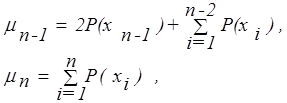
|
где n - число элементов в Х (или мощность конечного множества Х); mi - степень принадлежности xi нечеткому множеству А; Р(xi) - вероятность того, что в проводимом эксперименте будет выбран элемент xi. Заметим, что mn =1 тогда и только тогда, когда вероятность пустого множества равна нулю, т.е. (m1= 1) « (РÆ = 0).
Из системы уравнений (3.12) видно, что если известны вероятности, с которыми в проводимом эксперименте выбираются элементы множества Х, то эту информацию можно использовать для определения степеней принадлежности элементов к нечеткому множеству А. Оценка вероятностей Р(xi) и последующее определение степеней принадлежности mi осуществляется по методике, опирающейся на семантическую выборку уровневых множеств.
1. С каждым xi связывают величину Тi, первоначально равную 0, а в последующем - числу появлений хi..
2. Определяется объем выборки М, необходимый для успешной работы, например, М=25, М=50, М=100.
3. Интервал [0, 1] делится на М частей равной длины, например, при М=50 получим, {1; 0,98; 0,96; 0,94; ... ; 0,02}; полученное множество обозначается через S.
4. Случайным образом без возврата выбирается элемент a из S, т.е. случайно берется значение уровня a.
5. Перечисляются все элементы из Х, которые, по мнению исследователя (эксперта), принадлежат множеству, соответствующему выбранному значению множеству a.
6. При каждом появлении элемента на выбранном множестве Тi добавляется 1/k, где k - число элементов, включенных в множество уровня a.
7. Процедуры 4-6 повторяются до тех пор, пока не используются все a в S.
8. Определяются Р(xi) = Тi /М.
9. Полученные оценки вероятности упорядочивают по возрастанию и подставляют в (3.12), рассчитывая степени принадлежности элементов множества Х нечеткому множеству А.
Пример 3.4. Дегустатору предложили оценить шесть сортов вин, скажем, a, b, c, d, e, f с точки зрения их принадлежности понятию “вкуснее”. Нужно получить степени принадлежности {a, b, c, d, e, f} = X нечеткому множеству А, выраженному понятием “вкусное вино”. Возьмем объем выборки М = 25, тогда S = {1; 0,96; 0,92; ...; 0,08; 0,04}. Выбирая значения уровня a из S случайным образом, дегустатор представил следующие уровневые множества нечеткого множества А:
| Х0,92 = {d}, | X0,52 = {e, b, d}, |
| Х0,6 = {e, b, d}, | X0,40 = {c, a, e, b, d}, |
| Х0,36 = {c, a, e, b, d}, | X0,12 = {c, a, e, b, d}, |
| Х0,32 = {c, a, e, b, d}, | X0,80 = {b, d}, |
| Х0,72 = {b, d}, | X0,64 = {e, b, d}, |
| Х0,44 = {a, e, b, d}, | X0,56 = {e, b, d}, |
| Х0,88 = {b, d}, | X1,00 = {d}, |
| Х0,08 = {f, c, a, e, b, d}, | X0,28 = {e, a, c, d, b}, |
| Х0,84 = {b, d}, | X0,16 = {c, a, e, b, d}, |
| Х0,04 = {f, c, e, d, b, a}, | X0,20 = {c, a, e, b, d}, |
| Х0,68 = {e, b, d}, | X0,48 = {a, e, b, d}, |
| Х0,24 = {e, a, c, d, b}, | X0,96 = {d}. |
| Х0,76 = {b, d}. |
Используя полученные данные, можно подсчитать Тi для каждого элемента:
Та = 2×1/6 + 8×1/5 +2×1/4 = 2,433,
Tb = 2×1/6 + 8×1/5 +2×1/4 + 5×1/3 + 5×1/2 = 6,6,
Tc = 2×1/6 + 8×1/5 = 1,933,
Td = 2×1/6 + 8×1/5 +2×1/4 + 5×1/3 + 5×1/2 + 3 = 9,6,
Te = 2×1/6 + 8×1/5 +2×1/4 + 5×1/3 = 4,1,
Tf = 2×1/6 = 0,33.
По значениям Тi оцениваются вероятности: (Р(xi) = Тi /25 ):
| Р(а) = 0,097; | P(b) = 0,264; | P(c) = 0,077; |
| P(d) = 0,384; | P(e) = 0,164; | P(f) = 0,013 |
и располагаются в возрастающем порядке: P(f); P(c); P(a); Р(e); P(b); P(d).
Путем подстановки полученных значений Р(xi) в (3.12) и, учитывая, что n=6, определяются степени принадлежности элементов xi множеству А.
| mf =6 P(f) = 0,078, |
| mc = 5P(c)+ P(f) = 0,398, |
| ma = 4P(a) + P(f) + P(c) = 0,478, |
| me = 3P(c) + P(а) + P(c) + P(f) = 0,678, |
| mb = 2P(b) + P(e) + P(a) + P(c) + P(f) = 0,879, |
| md = P(d) + P(b) + P(e) + P(a) + P(c) + P(f) = 1. |
Следует отметить, что данный метод улучшает оценки mi при увеличении выборки М.
Прямые методы для группы экспертов предполагают, некоторый интегрированный учет мнений всех экспертов о виде соответствия между степенями принадлежности и элементами множества Х. Рассмотрим один из наиболее простых прямых групповых методов.
Пусть часть (N1) из N экспертов на вопрос о принадлежности элемента хÎ Х нечеткому множеству А отвечает положительно. Другая часть (N2) экспертов отвечает на этот вопрос отрицательно. При этом N1+N2=N. Тогда значение функции принадлежности элемента х множеству А может приниматься как отношение, определяющее своего рода частотную вероятность
| mА(х) = N1 /N. | (3.13) |
Такая методика определения функции принадлежности имеет смысл, если одновременно строится функция принадлежности нечетких множеств, задающих нечеткие значения из терм-множества Тb лингвистической переменной b. В этом случае результаты опроса можно свести в таблицу (табл.3.1).
Таблица 3.1.Исходные данные группового опроса экспертов
| Экс- | Термы и их значения | ||||||||||||||||
| перт | Т1(a1) | ... | ТJ(aJ) | ... | ТS(aS) | ||||||||||||
| nk | x1 | ... | x2 | ... | xm | ... | x1 | ... | xi | ... | xm | ... | x1 | ... | x2 | ... | xm |
| n1 | p111 | ... | p 1i1 | ... | p1m1 | ... | p11j | ... | p1ij | ... | p1mj | ... | p11S | ... | p1iS | ... | p1mS |
| n2 | p 211 | ... | p 2i1 | ... | p2m1 | ... | p21j | ... | p2ij | ... | p2mj | ... | p21S | ... | p2iS | ... | p2mS |
| ... | |||||||||||||||||
| nk | p k11 | ... | pki1 | ... | pkm1 | ... | pk1j | ... | pkij | ... | pkmj | ... | pk1S | ... | pkiS | ... | pkmS |
| nN | pN11 | ... | pNi1 | ... | pNm1 | ... | pN1j | ... | pNij | ... | pNmj | ... | pN1S | ... | pNiS | ... | pNmS |
Тогда для Тj
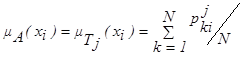
| (3.14) |
при
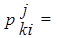
| 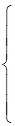
| 1, когда k - эксперт отнес х со значением хi к нечеткому множеству А, обозначенному термом Tj, имеющим лингвистическое значение aj; 0 в противном случае. |
Каждый эксперт должен однозначно отдать предпочтение по принадлежности хi к одному из Тj , т.е.
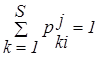 . .
| (3.15) |
В более общем случае данного метода оценкам экспертов сопоставляются весовые коэффициенты аk Î[0, 1], отражающие степень компетентности экспертов. В этом случае:
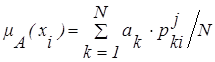 . .
| (3.16) |
Процедура введения аk повышает достоверность, однако требует привлечения дополнительных экспертов для оценки предыдущих, и т.д.
В рассмотренном методе степень принадлежности имеет, как правило, вероятностную интерпретацию, т.е. степенью принадлежности является вероятность того, что эксперт отнесет элемент к множеству А, обозначенному термом, или, что есть вероятность того, что эксперт использует понятие А в качестве имени объекта.
Существует и такой метод, когда для каждого элемента xi значение функции принадлежности mТ1(xi) дополняет до единицы значение функции принадлежности mТ2(xi) (в случае двух термов: Т1 и Т2 когда терм-множество состоит из двух противоположных термов, например, “большой” и “маленький”, “высокий” и “низкий” и т.п.). Если число термов j > 2, то эксперты оценивают вероятность xi в каждом терме терм-множества. При этом выполняется (3.16).
Предполагаются расчетные варианты получения функции принадлежности mТj(xi), используя равенство mТj(xi) = P(Tj /xi), где условная вероятность определяется по формуле Байеса
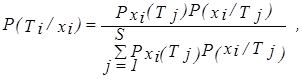
| (3.17) |
где
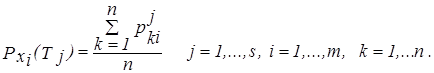
| (3.18) |
Наиболее сложным в данном варианте оказывается определение P(xi /Tj). Следует отметить, что рассмотренный метод групповой оценки степени принадлежности и его варианты можно одинаково успешно применять при наличии базовой шкалы или базового множества.
Отношение четких и нечетких величин может быть задано функцией принадлежности. Построим функцию принадлежности нечеткого числа «»»некоторому четкому числу, используя метод определения параметров заранее заданной функции, опирающийся на понятие рызмытости нечеткого множества, рассмотренное в п.2.5.
Эксперты должны отыскать параметры заранее заданной экспоненциальной функции, при решении задачи используются результаты экспертного опроса.
Для построения функции принадлежности будем использовать функцию вида: 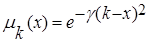 , где g зависит от требуемой степени нечеткости и определяется выражением:
, где g зависит от требуемой степени нечеткости и определяется выражением:
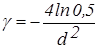 , ,
| (3.19) |
где d - расстояние между точками перехода для функции m(х), т.е. точками, в которых функция принадлежности принимает значение 0,5.
Следуют выяснить, как эксперты представляют себе границы классов чисел » k. Для этого проводим статистические исследования. 9 экспертам предлагаем назвать такие a(k) и b(k), которые, по их мнению, отделяют числа «»» заданному k от чисел таковыми не являющимися.
Рассмотрим натуральное число k. Пусть его младшая значащая цифра имеет порядок q. Разобьем возможные значения q на классы вычетов по модулю 3, и введем переменную d1 , значения которой будут являться представителями данных классов. Получим классы эквивалентности.
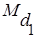 = {0, 1, 2} -множество классов.
= {0, 1, 2} -множество классов.
Введем целочисленную переменную J, изменяющуюся в пределах от 1 до 99, и будем считать, что для каждого ее значения известны параметры a(J) и b(J). На основании результатов опроса выяснилось, что значение d(J) в зависимости от J можно находить, как показано в табл.3.2.
Таблица 3.2. Зависимость расстояния между точками от переменной J, d(J)
| J | d(J) |
| 1, 2, 3, 4, 6, 7, 8, 9 | 0,46 *J |
| 10, 20, 30, 40, 60, 70, 80, 90 | (0,375-0,00163 *J)* J |
| 35, 45, 55, 65, 75, 85, 95 | (0,213-0,00067* J)* J |
| 5 | 2,8 |
| 15 | 6,48 |
| 25 | 6,75 |
| 50 | 24 |
| Прочие двухзначные числа | 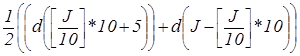 ,
где [ ] - целая часть ,
где [ ] - целая часть
|
Значения d(J) зависит и от того, какому классу » число k. Обозначим через rq цифру, стоящую в q-м разряде числа k, тогда:
1) KÎM0 - это значит, что при делении числа К на 3, остаток равен 0;
В этом случае d(K) зависит только от младшей значащей цифры числа K - rq:
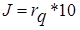 , , 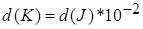
| (3.20) |
2) KÎM1, (d1=1)
а) 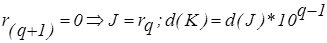 ;
;
б) 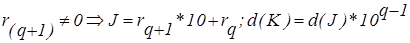 ;
;
3) KÎM2,
а) 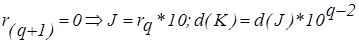 ;
;
б) 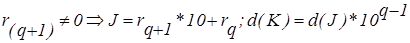 ;
;
После того, как для числа K найдено значение d(K) строим функцию принадлежности m.
Пример 3.5. Имеем примерно равную точечную оценку параметра х»235. Таким образом, k = 235. Разложим число 235 по разрядам. q = 1; rq = r1 = 5; rq+1 = r2 = 3.
При делении числа q на 3 получили, 1 - остаток Þ K Î M1Þ рассматриваем вариант - 2б. Осуществим расчет параметров:
I = rq2 * 10 + rq1 = 3*10 +5 = 35;
d(I) = (0.213 - 0.00067*I)*I = (0.213 - 0.00067*35)*35 = 6.634;
d(k) = g(I) * 10q-1 = 6.634*100 = 6.634;
g = - (4*ln0.5)/6.6342 = 0.063;
Исходя из представленных результатов функция принадлежности примет вид: 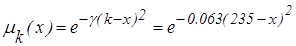 .
.
Пример 3.6. Построить функцию принадлежности нечеткого множества, определяющего величину, принимающую значения в интервале [8, 11].
На интервале [8, 11] функция принадлежности m(x) =1, а за его пределами будет повторять функции принадлежности соответствующие точечным оценкам «х=8» и «х=11».

Рис.3.4. Функция принадлежности трапециевидного числа
1. К=8, q=1, rq=r1=8, rq+1=rq2=0. При делении q на 3 получаем остаток 1.
d1=1, KÎM1Þ рассматриваем вариант - 2a.
Осуществим расчет параметров:
J=rq=8, d(J)=0,46*8=3,68
d(K)=3,68*100 =d(J)=3,68
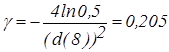 Þ
Þ 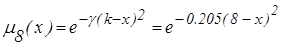 .
.
2. К=11, q=1, rq=r1=1, rq+1=rq2=1. При делении q на 3 получаем остаток 1.
d1=1, KÎM1Þ рассматриваем вариант - 2б.
Осуществим расчет параметров:
J=rq+1*10+rq=11,
d(K)= d(J)*100 =d(J) :
d(J)= 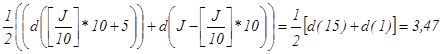 .
.
d(K)=3,47*1=3,47
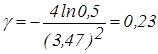 Þ
Þ 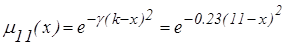 .
.
3. Определим границы интервала a и b:
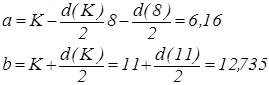
При использовании рассмотренныго выше метода становится возможным сравнение точности результатов, полученных для различных моделей. Анализируя интервалы или функции принадлежности для полученных в результате расчетов величин, можно доказать преимущество одной из моделей в данной ситуации.
Дата добавления: 2021-10-28; просмотров: 792;











