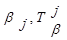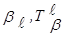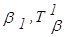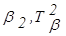Представление нечеткой и лингвистической переменных в ЭВМ
Прикладные исследования, проводимые в различных направлениях творческой деятельности, показали неспособность обычных методов анализа систем и моделирования на ЭВМ, основанных на точной обработке численных данных, в должной мере отразить огромную сложность и многообразие реальных процессов, явлений и объектов. Одним из преткновений на пути использования нечетких и лингвистических переменных, позволяющих расширить представление о реальных процессах, явлениях и объектах, повысить их информационное содержание, является недостаточная приспособленность традиционных моделей и баз данных к восприятию таких переменных и их последующему анализу. Попытаемся найти пути реализации этой проблемы.
Как было указано ранее, нечеткая и лингвистическая переменные представляются в виде кортежей соответственно:
| < a, X, Ca>, | (3.35) |
| <b, Tb , X>. | (3.36) |
Рассмотрим отдельно эти переменные в зависимости от характера их базового множества, т.е. когда Х представляется дискретным конечным множеством и когда Х является непрерывным множеством, расположенным на оси действительных чисел R (континуум).
Для дискретного Х, когда SA = {xi}, целесообразно первое поле реляционной базы данных заполнить SA = {xi}, где хÎХ, а следующее поле с индексом a заполнить элементами ma(хi) с учетом связи Ca=<ma(хi) /хi>. Так как Ca фактически отражает семантику, то можно утверждать, что в указанном виде нечеткая переменная будет полностью представлена. Более того, если на одном базовом множестве располагается несколько нечетких переменных хak (часто встречающийся на практике случай), то такая форма представления (табл.3.8) и в этом случае окажется приемлемой при условии
| Cak = < ma k(хi) /хi > = <mik /хi>. | (3.37) |
Последовательная группировка ak по терм-множествам
| Тb¢ = {Т11 = a1, Т21 = a2, ... , Тs1 = as1 }, Тb2 = {Т12 = ak+1, ... , Тs2 = ak+s2} . . . . . . . . . . . . . . . | (3.38) |
дает возможность представления в указанной базе данных лингвистических переменных b (табл.3.8).
Таблица 3.8. Представление нечетких и лингвистических переменных при дискретном
Базовом множестве
| Х (SA) | a1 | a2 | a3 | a4 | a5 | a6 | … | ak | … | am-1 | am | ||||||||
| x1 | m11 | m12 | m13 | m14 | m15 | m16 | … | m1k | … | m1,m-1 | m1m | ||||||||
| … | … | … | … | … | … | … | … | … | … | … | … | ||||||||
| xi | mi1 | mi2 | mi3 | mi4 | mi5 | mi6 | … | mik | … | mi,m-1 | mim | ||||||||
| … | … | … | … | … | … | … | … | … | … | … | … | ||||||||
| xn | mn1 | mn2 | mn3 | mn4 | mn5 | mn6 | … | mnk | … | mn,m-1 | mnm | ||||||||
 
  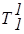
| 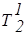
| 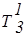
| 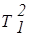
| 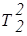
| 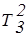
| 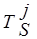
|  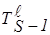
| 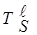
| |||||||||||
Предлагаемая форма представления нечетких и лингвистических переменных не исключает комбинированного отображения состояния предметной области посредством реляционной модели базы данных. Такая возможность иллюстрируется примером (табл.3.9).
Таблица 3.9. Пример реляционной базы
| Студ. группа | Факультет | Специальность | Кол-во студентов | Сильная | Слабая | Ровная | Дружная |
| 1-51 | ИФ | 41.01 | 0,8 | 0,2 | 0,7 | 0,8 | |
| 1-52 | ИФ | 41.02 | 0,4 | 0,7 | 0,6 | 0,5 | |
| … | … | … | … | … | … | … | … |
| 1-61 | МФ | 18.01 | 0,3 | 0,8 | 0,5 | 0,3 | |
| … | … | … | … | … | … | … | … |
Для непрерывного базового множества ХÌ R степени принадлежности mik могут определяться через полученные тем или иным методом функции принадлежности mА(х)=ma(х). При этом возникает задача, как хранения функции принадлежности, так и оперативного представления ее значений при изменении хÎR. Это может быть осуществлено при условии аппроксимации экспериментально полученной функции принадлежности. В общем случае функция принадлежности (рис.3.20) может быть аппроксимирована выражением (3.39).
m(х)

|
а в
Рис.3.20.Общий случай представления функции принадлежности m(х)
|
| m(x)= | 
| Æ при х £ х1 (А - а sin 2pА)e при х1< х< х10 1 при x10 £ x £ x20 (B - b sin 2pB)e при х20< х< х2 Æ при х2< х, | (3.39) |
где 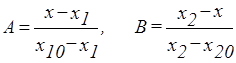 ;
;
а, в - аппроксимирующие коэффициенты;
sup (a, b) = 1/2p, inf (a, b) = 0;
e - коэффициент концентрации (e >1) или растяжения (e < 1).
Из (3.39) следует, что любую, полученную экспериментальным путем функцию принадлежности m(х), можно охарактеризовать кортежем
| < x1, x10, x20, x2, a, b, e >. | (3.40) |
Универсальность выражения (3.39) и кортежа (3.40) подтверждается иллюстрацией (рис.3.21).

m(х )
х
а) б) в) г) д)
 m(х)
m(х)

х

е) ж) з) и) к) л)
Рис.3.21. Различные варианты представления функции принадлежности m(х)
при следующих значениях характеристик кортежа (3.40):
а) (x10– x1) = (x2- x20), x20> x10, a > 0, b > 0, e = 1,
б) (x10- x1) < (x2- x20), x20= x10, a > 0, b > 0, e = 1,
в) (x10- x1) = (x2- x20), x20= x10, a > 0, b > 0, e = 1,
г)(x10- x1) < (x2- x20), x20> x10, a = 0, b = 0, e = 1,
д)(x10- x1) = (x2- x20), x20> x10, a = 0, b = 0, e = 1,
е) (x10- x1) > (x2- x20), x20= x10, a = 0, b = 0, e = 1,
ж) (x10- x1) = (x2- x20), x20= x10, a = 0, b = 0, e = 1,
з) x10= x1, x2> x20, x20> x10, a = 0, b > 0, e = 1,
и) x10> x1, x2= x20, x20> x10, a = 0, b = 0, e = 1,
к) (x10- x1) = (x2- x20), x20= x10, a = 0, b > 0, e = 1,
л) x10= x1 , x2= x20, x20> x10, a = 0, b = 0, e = 1.
Влияние e на характер функции принадлежности представлено на рис.3.22.
 m(х)
m(х)
e < 1
e =1
e > 1
х1 х10 х20 х2 х
Рис.3.22. Представление m(х) при e =1 и e ¹1
Это влияние можно использовать как при аппроксимации экспериментально полученной функции принадлежности, так и при изменении требований принадлежности х к понятию А, появляющихся при возникновении различных ситуаций. В таких случаях eпредставляется как функция от одного или нескольких факторов, определяющих суть ситуации, т.е.
| e = j(у1, у2, ..., уk). | (3.41) |
В отдельных случаях eможет изменяться путем переназначения.
Пример 3.9. При оценке стоимости продуктов в задачах экономического анализа и прогнозирования возможно использование лингвистической переменной b - “стоимость продуктов” с терм-множеством Тb = <”низкая”, “средняя”, “высокая”>. Известно, что оценка стоимости продуктов зависит от темпов инфляции. Эта зависимость может быть выражена через функцию e = j(у) вида
e = k(D I’ /D I”),
где D I’, D I” – темпы инфляции (предшествующий и рассматриваемый периоды). Данное выражение определяет семантическое правило М лингвистической переменной b, при котором с увеличением темпов инфляции оценка стоимости продуктов становится более растяжимой (2.17), а с уменьшением – более стабильной, концентрированной (2.16).
Процесс определения, аппроксимации и машинной реализации функции принадлежности, а также ее модернизации представлены схемой (рис.3.23).
ЭВМ

Ввод МФ
|
|
Yi


 j(yi)
j(yi)


|


|

|
|











|
|




|
|

|
|

 b anТb x1х10 x20 x2a b e
b anТb x1х10 x20 x2a b e
Рис.3.23. Схема формирования и представления функции принадлежности m(х)
для непрерывного Х
Полученные экспериментальным путем функции принадлежности mAэ(х), характеризующие нечеткую переменнуюa или термы множества Тb лингвистической переменной b, аппроксимируются кортежем (3.40). Значения величин, входящих в кортеж (3.39), заносятся в базу индексов и параметров нечетких и лингвистических переменных (БИП). Ввод коэффициента e осуществляется непосредственно или косвенно по значениям уi через модуль функции (3.41) (МФ). По значению х для соответствующей a или b с помощью расчетно-логического модуля (РЛМ), реализующего (3.39), определяется степень принадлежности m(х).
Контрольные вопросы
1. В чем заключается содержание функции принадлежности?
2. Каковы характерные особенности прямых и косвенных методов построения функции принадлежности?
3. Каковы достоинства и недостатки метода непосредственного назначения mА(х)?
4. Каким образом определяется функция принадлежности при использовании метода семантических дифференциалов?
5. В каких случаях целесообразно использовать метод частичной принадлежности?
6. Для решения, каких задач применяется метод построения функции принадлежности на основе интервальных оценок?
7. Каким образом определяется функция принадлежности при использовании метода определения параметров заранее заданной функции?
8. Как реализовать на ЭВМ метод уровневых множеств?
9. Какие достоинства и благодаря чему имеют групповые прямые методы по сравнению с индивидуальными?
10. Как выражаются достоинства косвенных методов в методе попарных сравнений, предложенном Т. Саати?
11. Для чего и каким образом можно представить m(х) в ЭВМ?
12. В чем заключается метод построения терм-множеств, каковы его достоинства и недостатки?
Дата добавления: 2021-10-28; просмотров: 450;