Многозначная логика
В известной двухзначной логике каждому логическому высказыванию или формуле приписывается значение “истина” или “ложь”. Такая категоричность редко встречается в реальных суждениях: как правило, люди бывают не столь категоричны и свои выводы делают на основании более гибкого, более расплывчатого подхода. Это, в первую очередь, отражается в оценке истинности. В связи с этим в многозначной логике высказываниям или формулам как исходным, так и получаемым в результате логических операций, их истинностное значение определяется не из кортежа {0,1}, а из интервала [0,1]. Величину vÎ[0,1] называют степенью истинности логического высказывания или формулы.
Как и в двузначной логике, нечеткие высказывания бывают простыми и сложными, или составными. К простым высказываниям можно отнести такие высказывания, как:
А - “Небо голубое”,
В - “Очередь маленькая”,
С - “Студент хорошо учится”.
В двузначной логике этим высказываниям придаются два возможных значения: “истина” или “ложь”. При использовании нечеткой информации каждому утверждению можно придавать степень принадлежности истинному высказыванию или степень истинности vÎ[0,1], т.е. v(A)=mAÎ[0,1], v(B)=mBÎ[0,1], v(C)=mCÎ[0,1].
Сложные, или составные, высказывания образуются с помощью логических операций отрицания, дизъюнкции, конъюнкции и др. Следует отметить, что в зависимости от трактовки теории нечетких множеств эти операции могут иметь различный характер. Здесь в первую очередь можно отнести нечеткую логику с минимаксными операциями (К – стандартная последовательная логика, основанная Л. Заде), вероятностную нечеткую логику и нечеткую логику с ограниченными операциями (t - логика или логика Лукасевича). Для каждой из этих логик при выполнении операций существуют свои правила определения степени истинности v для составных высказываний (см. табл.4.1), где Р и Q - простые высказывания, а p и q - их степени истинности.
Во всех случаях значения отрицания вычисляются по формуле v(ù P)=1-v(P), значение импликации по формуле v(P®Q)=v(ù PÚQ ), значение эквивалентности по формуле (P«Q)=v(P®Q)&(Q®P). Связки ex, ç и ¯ определяются как отрицания «,&,Úсоответственно. Тавтология и противоречие соответственно будут:
v( 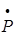 ) = v(PÚù P), v (
) = v(PÚù P), v ( 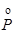 ) = v(P&ù P),
) = v(P&ù P),
или в общем виде:
v( 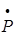 Q) = v((PÚù P) Ú (QÚù Q)),
Q) = v((PÚù P) Ú (QÚù Q)),
v( 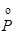 Q)= v((P&ù P) Ú (Q&ù Q)).
Q)= v((P&ù P) Ú (Q&ù Q)).
Таблица 4.1. Определение степени истинности для составных высказываний
| Название связи | Обозначение связи | Правила определения V(P,Q) | ||
| Нечеткая логи-гика с минимаксными операциями | Вероятностная не- четкая логика | Логика Лукасевича (с ограниченными операциями) | ||
| Отрицание | ù P | 1-p | 1-p | 1-p |
| Дизъюнкция | PÚ Q | max(p,q) | p+q-pq | min(1,q+p) |
| Конъюнкция | P&Q | min(p,q) | pq | max(0,p+q-1) |
| Импликация | P®Q | max(1-p,q) | 1-p+pq | min(1,1-p+q) |
| Эквивалентность | P«Q | min[max(1-p,q), max(p,1-q)] | 1-½p-q½ | (1-p+pq)(1-q+pq) |
| Штрих Шеффера | P½Q | max(1-p,1-q) | 1-pq | min(1,1-p+1-q) |
| Исключающее “Или” (разделительная дизъюнкция) | PexQ | max[min(1-p,q), min(p,1-q)] | 1-(1-p+pq)(1-q+pq) | ½p-q½ |
| Стрелка Пирса | P¯Q | min(1-p,1-q) | (1-p)(1-q) | max(0,1-p-q) |
| Тавтология | 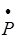
| max(p,1-p) | 1-p(1-p) | 1 |
| Противоречие | 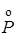
| min(p,1-p) | p(1-p) | 0 |
В первой логике дизъюнкция и конъюнкция определяются по правилу:
v(P&Q)=min(v(P),v(Q)),
v(PÚQ)=mах(v(P),v(Q))
и являются коммутативными, ассоциативными, идемпотентными и дистрибутивными относительно друг друга, но не удовлетворяющие закону исключенного третьего: v(PVù P)¹1 и v(P&ù P)¹0.
В вероятностной логике операции
v(PÚQ)= v(P) + v(Q) - v(P) v(Q),
v(P&Q) = v(P) v(Q)
являются коммутативными, ассоциативными, но не идемпотентными и не дистрибутивными относительно друг друга.
Для логики Лукасевича операции определяются как
v(PÚQ)= min(1,v(P),+v(Q)),
v(P&Q) = max(0,v(P) + v(Q-1)
и являются коммутативными и ассоциативными, но не идемпотентны и не дистрибутивны друг относительно друга; закон исключенного третьего удовлетворяется.
В составном нечетком высказывании порядок выполнения операций определяется скобками, а при их отсутствии сначала выполняется отрицание, затем конъюнкция, далее дизъюнкция и, наконец, импликация, эквивалентность, другие операции.
Обратим внимание, что два высказывания P и Q называются нечетко близкими, если степень истинности высказывания P « Q v(P « Q) ³ 0,5. При v(P « Q)=0,5 высказывания P и Q называют нечетко индифферентными.
Рассмотренные операции составляют основу нечеткой или многозначной логики.
Обратимся к понятиям нечеткая логическая формула и входящая в нее нечеткая пропозициональная или, как еще называют, высказывательная переменная. Под нечеткой высказывательной переменной xi в общем виде понимают нечеткое высказывание, степень истинности которого может принимать произвольное значение из замкнутого интервала [0,1]. В качестве нечеткой переменной могут выступать ранее рассмотренные как нечеткая (a), так и лингвистическая (b) переменные.
Нечеткой логической формулой f(x1, x2, ..., xn), где n³1, называется:
1) число (константа) из интервала [0,1],
2) любая нечеткая переменная xi ,
3) выражение f(x1,x2,...,xn), полученное из нечетких логических формул f1(x1, x2, ..., xn) и f2(x1, x2, ..., xn) приложением к ним любого конечного числа логических операций.
Для любых двух нечетких логических формул f1(x1,x2,...,xn) и f2(x1, x2,...,xn), которые определены на наборах нечетких переменных x1,x2, ..., xn, вводится фундаментальное понятие степени их равносильности, которое является обобщением понятия равносильности четких логических формул.
Степень равносильности формул f1(x1, x2, ..., xn) и f2(x1, x2, ..., xn) обозначается v(f1, f2) и определяется выражением
v(f1, f2) = 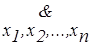 (f1(x1, x2, ..., xn) « f2(x1, x2, ..., xn)) . (f1(x1, x2, ..., xn) « f2(x1, x2, ..., xn)) .
| (4.1) |
Если степень равносильности v(f1, f2) на всех определенных наборах степе-ней истинности нечетких переменных xi больше или равна 0,5(v(f1, f2)³0,5),то такие формулы будем называть нечетко близкими на этих наборах и обозначать
|
 f2(x1, x2, ..., xn) .
f2(x1, x2, ..., xn) .
В случае, когда v(f1, f2)£ 0,5, считается, что формулы f1 и f2 не являются нечетко близкими на этих наборах, т.е.
f1(x1, x2, ..., xn) = f2(x1, x2, ..., xn) .
Если v(f1, f2)=0,5, то формулы f1и f2одновременно являются и не являются нечетко близкими. Их называют взаимно индифферентными и обозначают
f1(x1, x2, ..., xn) ~ f2(x1, x2, ..., xn) .
Понятие равносильности четких логических формул является частным случаем нечеткой близости. Если нечеткие формулы f1и f2на одних и тех же наборах степеней истинности переменных принимают одни и те же значения степеней истинности, то значение степени их равносильности всегда ³ 0,5, что также является частным случаем нечеткой близости.
Пример 4.1.Определим степень равносильности формул f1(x1, x2)=ù x1® x2 и f2(x1, x2)= x1&ù ® x2 при условии, что x1принимает значения степеней истинности из множества дискретных значений {0,8;0,6;0,7}, а x2- из множества {0,3;0,4}. Степень равносильности данных формул в общем виде определяется выражением
v(f1,f2) = 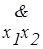 ((ù x1® x2)«( x1&ù x2)).
((ù x1® x2)«( x1&ù x2)).
Выбирая все возможные наборы степеней истинности переменных x1 и x2 и используя правила определения степеней истинности для составных высказываний (табл.4.1), получим:
v(f1,f2)=(( 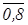 ® 0,3)«(0,8 &
® 0,3)«(0,8 & 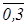 ))&((
))&(( 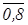 ® 0,4)«(0,8 &
® 0,4)«(0,8 & 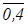 ))&((0,6® 0,3)«
))&((0,6® 0,3)«
«(0,6 & 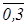 )) & ((
)) & (( 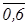 ® 0,4) «(0,6 &
® 0,4) «(0,6 & 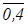 )) & ((
)) & (( 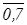 ® 0,3) «(0,7 &
® 0,3) «(0,7 & 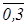 )) &
)) &
& (( 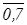 ® 0,4) « (0,7 &
® 0,4) « (0,7 & 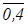 )) = (0,8 « 0,7) & (0,8 « 0,6) & (0,6 « 0,6) &
)) = (0,8 « 0,7) & (0,8 « 0,6) & (0,6 « 0,6) &
& (0,6 « 0,6) &(0,7« 0,7)&(0,7« 0,6)=0,7&0,6 & 0,6 & 0,6 &0,7&0,6= 0,6.
Это означает, что формулы f1и f2нечетко близкие на заданных наборах степеней истинности высказывательных переменных x1и x2.
Определим степень равносильности этих же формул, принимая значение степеней истинности из множества {0,2;0,4} для x1и множества {0,6;0,7;0,8} для x2:
v(f1,f2)=(( 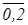 ®0,6) «(0,2&
®0,6) «(0,2& 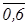 ))&((
))&(( 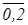 ®0,7)«(0,2& 0,7)) &((
®0,7)«(0,2& 0,7)) &(( 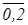 ® 0,8) «
® 0,8) «
«(0,2 & 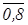 )) & ((
)) & (( 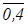 ® 0,6) «(0,4 &
® 0,6) «(0,4 & 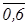 )) & ((
)) & (( 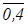 ® 0,7) «(0,4 &
® 0,7) «(0,4 & 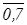 )) &
)) &
& (( 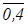 ® 0,8) « (0,4 &
® 0,8) « (0,4 & 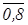 )) = (0,6 « 0,2) & (0,7 « 0,2) & (0,8 « 0,2) &
)) = (0,6 « 0,2) & (0,7 « 0,2) & (0,8 « 0,2) &
& (0,6« 0,4)&(0,7«0,3) &(0,8« 0,2)=0,4&0,3 &0,2& 0,4 & 0,3 & 0,2 = 0,2.
На этих наборах степеней истинности f1 и f2 не являются нечетко близкими.
Итак, нечетко близкими можно считать формулы f1({xi}) и f2({xj}) i,jÎ I, для которых
"{xi}${xj}, n( f1f2) = 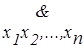 (f1{xi} « f2{xj}) ³ 0,5. (f1{xi} « f2{xj}) ³ 0,5.
| (4.2) |
Если при всех определенных значениях степеней истинности нечетких переменных х значение степени истинности нечеткой логической формулы f(x) больше или равно 0,5, то такую формулу называют нечетко истинной, или общезначимой, т.е. общезначимой (тавтологией) считается логическая формула f1({xi}), если
| "{ xi } "n({ xi }), n(f) ³ 0,5. | (4.3) |
В случае когда
| "{ xi } " n({ xi }), n(f) £ 0,5, | (4.4) |
логическую формулу n(f) называют нечетко ложной, или противоречивой (противоречием).
Простейшими нечетко истинными (тавтологиями) и нечетко ложными (противоречиями) являются логические формулы:
fи (xi ) = xi Ú 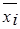 , ,
| (4.5) |
fл (xi) = xi & 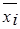 , ,
| (4.6) |
для которых n( fи) ³ 0,5, n( fл) £ 0,5 при "{xi}" n({хi}).
Если одна нечеткая логическая формула представлена в виде
f1({x}) = g1({x}) Ú fи(xi),
а другая в виде
f2({x}) = g2({x}) Ú fи(xj),
где g1 и g2 - некоторые нечеткие формулы от переменных {х}, а xi и xj - нечеткие переменные из набора {х}, то
| f1({x}) » f2({x}). |
Аналогичное утверждение можно сделать, если
f1({x}) = g1({x}) & fл(xi),
f2({x}) = g1({x}) & fл (xj).
Эти утверждения вытекают из (4.5) и (4.6) в случае минимаксной оценки степени истинности.
Если число нечетких переменных велико и перебор всех возможных соотношений между степенями истинности логических формул становится затруднительным, то для доказательства нечеткой близости можно использовать следующие свойства и выражения:
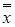 » х - двойное отрицание (инволюция), » х - двойное отрицание (инволюция),
| (4.7) | |
| х & x » x - идемпотентность для конъюнкции, х Ú х » х - идемпотентность для дизъюнкции, | (4.8) | |
| х & y » y & x - коммутативность для конъюнкции, х Ú y » y Ú х - коммутативность для дизъюнкции, | (4.9) | |
| х&(y&z)»(x& y)& z» x & y & z - ассоциативность для конъюнкции, хÚ(yÚz)»(х Ú y) Ú z » x Ú y Ú z - ассоциативность для дизъюнкции, | (4.10) | |
| х & (y Ú z) » (х & y) Ú (х & z) - дистрибутивность для конъюнкции, x Ú (y & z) » ( x Ú y) &(xÚz) - дистрибутивность для дизъюнкции, | (4.11) | |
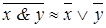 - инверсия (правило де Моргана) для конъюнкции, - инверсия (правило де Моргана) для конъюнкции,
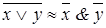 - инверсия (правило де Моргана) для дизъюнкции, - инверсия (правило де Моргана) для дизъюнкции,
| (4.12) | |
| х & (х Ú y) » х, х Ú (х & y) » х, | (4.13) | |
| (х Ú y) Ú (х & y) » х Ú y, (х Ú y) & (хÚ y) » х & y, | (4.14) | |
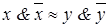 , ,
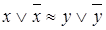 , ,
| (4.15) | |
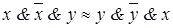 , ,
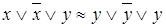 , ,
| (4.16) | |
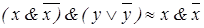 , ,
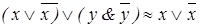 , ,
| (4.17) | |
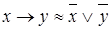 , ,
| (4.18) | |
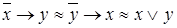 , ,
| (4.19) | |
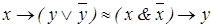 , ,
| (4.20) | |
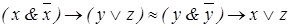 . .
| (4.21) | |
Если 0,1, с - константы, причем 0 < c < 1, то:
| х &0 » 0 , хÚ 0 » x, | х& 1 » х, х Ú 1 » 1. | (4.22) | ||
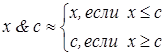 , ,
| 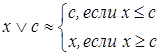 . .
| (4.23) | ||
Доказательство выражений (4.7)-(4.23) основывается на том, что степень равносильности v(f1,f2)³ 0,5. Это возможно в том случае, когда степени истинности формул v(f1) и v(f2) одновременно £ 0,5 или ³ 0,5 на одинаковых наборах переменных.
Пример 4.2. Следует доказать равносильность нечетких логических формул:
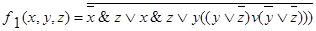 ,
,
f2(x,y,z) = (y&  )
) 
 .
.
Применив (4.12), получим:
f1(x,y,z)» (  &z
&z  x&z
x&z  (
(  &z)&(y& z))»(x
&z)&(y& z))»(x 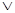
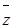 )&(
)&( 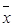
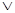
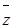 )&((y
)&((y 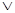
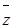 )v(
)v( 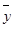
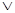
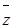 )).
)).
Используя (4.11), (4.8) и (4.9), приходим к соотношению:
f1(x,y,z) » ((x& 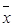 )Ú
)Ú 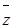 )&((yÚ
)&((yÚ 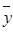 )Ú
)Ú 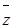 ).
).
При использовании (4.11) получим:
f1(x,y,z) » ((x& 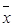 )&(yÚ
)&(yÚ 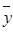 )Ú
)Ú 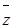 ).
).
После (4.8) имеем:
f1(x,y,z) » (x& 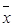 )Ú
)Ú 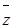 .
.
И, наконец, применив (4.15), получим
f1(x,y,z) » (y& 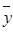 )Ú
)Ú 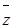 , что и требовалось доказать.
, что и требовалось доказать.
Нечеткие логические формулы могут быть определены не только на нечетких пропозициональных переменных, но и на каком-либо множестве X. Такие формулы также принимают значения на интервале [0,1]. Их называют нечеткими предикатами. Так функция принадлежности mА(x), рассмотренная при определении нечеткого множества А Í X, является одноместным нечетким предикатом, определенным на множестве X.
Пример 4.3. Пусть X={1,2,..., 10}. Нечеткий предикат Р(х) “быть небольшим числом” примет следующие значения: А(1)=1; А(2)=0,9; А(3)=0,6; А(4)=0,3; А(5) = 0,1; А(6 ) = 0, ... , представляющие нечеткое множество
А = {<1>, <0,9/2>, <0,6/3>, <0,3/4>, <0,1/5>}.
Пример 4.4. Пусть X = {1,2,3}; Y = {3,4,5}. Нечеткий предикат P(x, y) ”X немного меньше Y” примет следующие значения: P(1,3)=0,5; P(1,4)=0,1; P(1,5)=0; P(2,3)=1; P(2,4)=0,5; P(2,5)=0,1 и т.д.
Приведенные в данном разделе элементы многозначной логики дают некоторое представление о ее теоретических и практических возможностях. В первую очередь необходимо отметить обобщающий характер этой логики, при котором двоичная логика представляется как частная теория. Так, нечеткие формулы являются обобщением структуры булевых функций, так как удовлетворяют всем аксиомам последних (кроме закона о дополнении, т.е. fÚù f ¹1 и f &ù f ¹0.
В практическом плане многозначная логика расширяет возможности метода резолюций, используемого для построения систем логического вывода, экспертных систем. Большую роль играет многозначная логика в развитии такого важного в информатике направления, как распознавание образов, осуществляемое в целях классификации объектов и явлений в процессе принятия решений.
Если с помощью логических формул f1(x1, x2, ...,xn) и f2(x1, x2, ..., xn) дать описание двух объектов или явлений O1и O2соответственно, характеризуемых признаками x1, x2,...,xn , то на определенных наборах степеней истинности xi с помощью выражения (4.1) можно выяснить степень равносильности f1и f2, а следовательно, степень принадлежности O1и O2друг другу (или одному классу). Варьируя возможными наборами степеней истинности xi для O1и O2, можно найти наиболее оптимальные условия равносильности (нечеткой эквивалентности) O1и O2. Если при этом положить O1как эталон в принятии решения (эталон класса), то, при условии V(f2и f2) = 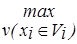 , можно рассматривать O2 как наиболее разумную альтернативу.
, можно рассматривать O2 как наиболее разумную альтернативу.
Использование свойств (4.7)-(4.23) позволяет нормирование сложных логических формул, упрощая аналитические процедуры.
Дата добавления: 2021-10-28; просмотров: 552;











