Нечеткозначная логика
Если многозначная логика описывается теорией нечетких множеств типа 1, то нечеткозначная логика - теорией нечетких множеств типа 2. Как было указано ранее (см. п.2.3), такая теория интерпретируется лингвистической переменной, значения которой определяются нечеткими переменными с соответствующим синтаксисом и семантикой. Определение истинности посредством лингвистической переменной приводит к нечеткой логике со значениями, подобными “истинно”, “не очень истинно”, “более менее истинно”, “очень истинно”, “совершенно истинно” и т.п. В связи с этим нечеткозначную логику иногда называют лингвистической логикой, а ее назначение тесно связывают с теорией приближенных рассуждений или приближенных решений, с поведенческой моделью принятия решений.
Для задания нечеткой истинности Заде предложил такие функции принадлежности термов "истинно" и "ложно":
| mистинно(x)= | 
| 0, | 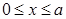
| |
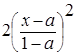 , ,
| 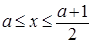
| |||
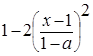 , ,
| 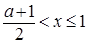
| |||
| mложно(x) = mистинно(1-x), хÎ [0,1]. |
где аÎ [0,1] - параметр, определяющий носители нечетких множеств "истинно" и "ложно". Для нечеткого множества "истинно" носителем будет интервал (a,1], а для нечеткого множества "ложно" - [0, а).
Функции принадлежности нечетких термов "истинно" и "ложно" изображены на рис. 4.1. Они построены при значении параметра а=0,4. Как видно, графики функций принадлежности термов "истинно" и "ложно" представляют собой зеркальные отображения.

Рис.4.1. Лингвистическая переменная "истинность" по Заде
Для задания нечеткой истинности Балдвин предложил такие функции принадлежности нечетких "истинно" и "ложно":
mистинно(x) =х;
mложно(x) =1-х,
где хÎ [0,1].
Квантификаторы "более-менее" и "очень" часто применяют к нечеткими множествами "истинно" и "ложно", получая таким образом термы "очень ложно", "более-менее ложно", "более-менее истинно", "очень истинно", "очень, очень истинно", "очень, очень ложно" и т.п. Функции принадлежности новых термов получают, выполняя операции концентрации и растяжения нечетких множеств "истинно" и "ложно". Операция концентрации соответствует возведению функции принадлежности в квадрат, а операция растяжения - возведению в степень ½. Следовательно, функции принадлежности термов "очень, очень ложно", "очень ложно", "более-менее ложно", "более-менее истинно", "истинно", "очень истинно" и "очень, очень истинно" задаются так:
m очень ложно (х)=( m ложно (х))2;
m очень, очень ложно (х)=( m очень ложно (х))2;
m более-менее ложно (х)=( m ложно (х))1/2;
m более-менее истинно (х)=( m истинно (х))1/2;
m очень истинно (х)=( m истинно (х))2;
m очень, очень истинно (х)=( m очень истинно (х))2.
Графики функций принадлежности этих термов показаны на рис.4.2.
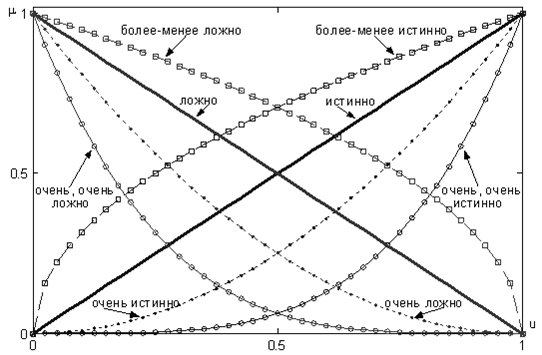
Рис.4.2.Лингвистическая переменная "истинность" по Балдвину
В нечеткозначной логике используются различные виды высказываний.
Основным является высказывание вида
| <b есть a>, | (4.24) |
где b - наименование лингвистической переменной, отражающей множество (класс) некоторых объектов и параметров реального мира и принимающей лингвистическое значение a в универсуме X; a - нечеткое подмножество X, которое индуцирует распределение возможности P(x) = a . Другими словами, если xÎ X º b и ma: x®[0,1] - функция принадлежности a, тогда возможность того, что X º b = x, задаваемое высказыванием <b есть a>, определяется как
| П{X:b=x | b есть a}= ma(x), xÎX. | (4.25) |
В качестве примеров высказывания вида (4.24) можно привести: <погода есть хорошая>, <температура есть высокая>, <девушка есть красивая>. Из последнего примера может быть получена следующая интерпретация выражения (4.25): “возможность того, что некая особа x (объект x), относящаяся к множеству (классу), названному b º<девушка> (путем измерения по шкале наименований или классификационной шкале), может получить значение <красивая>, равняется ее степени принадлежности ma(x) к нечеткому подмножеству a (красивые девушки) множества X”.
Введение оценки истинности v означает, что
| b есть a есть q « b есть g, | (4.26) |
где q - лингвистическое значение истинности, а g º a есть q. Здесь a, g и q связаны выражением
| q = ma(g). | (4.27) |
Это уравнение утверждает, что q есть образ g при отображении ma . Из этого следует, что
| mg(x) = mq(ma(x), | (4.28) |
т.е. оценка истинности v определяется как функция принадлежности к заданному лингвистически значению истинности функции принадлежности ma(x), определенной выражением (4.25). Так, при единичном значении истинности q =<истинно>
| mg(x) = ma(x) =v, vÎ[0,1]. | (4.29) |
При наличии mq
| v=mg(x) = ma +(x), | (4.30) |
где a+ - модификация a, индуцированная q.
Кроме основного вида высказываний (4.26) в нечеткозначной логике используются выражения, содержащие модификаторы, кванторы и композицию.
Высказывания, содержащие модификаторы, имеют вид:
| <b есть ma>, | (4.31) |
где m - модификатор такой, как “очень”, “примерно”, “более или менее”, “совсем”, “незначительно”, “не” и т.п. Определение истинности такого высказывания аналогично (4.30), где a+ - модификация a, индуцированная m.
Введение модификатора преобразует нечеткое подмножество a в a+, изменяя синтаксис и семантику лингвистической переменной соответственно по правилам G и M.
Семантика a+ определяется функцией принадлежности ma+, для описания которой можно использовать выражение (3.24). При этом происходит изменение значений составляющих кортежа лингвистической переменной.
В качестве примеров высказываний вида (4.31) можно отметить: <погода есть более или менее хорошая>, <температура есть не высокая>, <девушка есть очень красивая> и т.д.
Высказывания, содержащие кванторы, имеют вид
| <Q b есть a>, | (4.32) |
где Q - квантор такой, как “большинство”, “много”, “несколько”, “немного”, “некоторые” и т.п. Квантор Q определяет соответствующую пропорцию на множестве X. В отличие от кванторов " и $, используемых в исчислении предикатов первого порядка и означающих соответственно или “все x” , или “существует один x”, квантор Q может устанавливать промежуточные пропорции значений выбора x на множествах x ºb.
Примерами высказываний вида (4.32) являются <много девушек есть красивые>, <некоторые дни есть хорошие>, <большинство студентов есть успевающие> и т.д. Для сравнения можно привести смысл первого высказывания, квантифицированного с помощью " и $ : в первом случае получится <все девушки есть красивые>, во втором <есть такая девушка, которая красивая>.
Возможно комплексное использование m и Q
| <Q b есть ma>. | (4.33) |
Высказывания, содержащие композицию, состоят из различных сочетаний вышеприведенных высказываний, объединенных связками “И” (конъюнкция), “ИЛИ” (дизъюнкция), “ЕСЛИ ..., ТО ...” (импликация), “ЕСЛИ..., ТО..., ИНАЧЕ”. Например, <ЕСЛИ небо голубое ,ТО погода хорошая>, <ЕСЛИ небо голубое ИЛИ солнце яркое И ветер слабый, ТО погода очень хорошая> и т.д. Чтобы определить истинность таких сложных высказываний, необходимо привести их к виду (4.24), используя правила преобразования. Для этого представим два высказывания: <bX есть aX> и <bY есть aY> , где bX и bY - лингвистические переменные, определенные на множествах X и Y, а aX и aY - их значения с соответствующими нечеткими множествами
СX = {<mx(x)/x>} и СY = {<mY(y)/y>}.
Правило преобразования конъюнктивной формы имеет вид
<bX есть aX И bY есть aY> ® <(bX , bY) есть 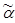 X Ç X Ç 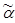 Y>. Y>.
| (4.34) |
Здесь выражение 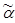 X Ç
X Ç 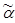 Y можно рассматривать как значение лингвистической переменной (bX, bY) с соответствующим нечетким множеством СÇ=
Y можно рассматривать как значение лингвистической переменной (bX, bY) с соответствующим нечетким множеством СÇ= 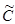 X Ç
X Ç 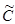 Y, где
Y, где 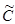 X и
X и 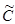 Y - цилиндрические продолжения нечетких множеств СX и СY.
Y - цилиндрические продолжения нечетких множеств СX и СY.
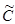 X = {<
X = {< 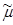 X(x,y)/x>};
X(x,y)/x>}; 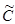 Y = {<
Y = {< 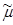 Y(x,y)/y>},
Y(x,y)/y>},
где (x,y)Î X ´ Y, причем ("xÎX)( "yÎY)[ 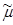 X(x,y) = mX(x)].
X(x,y) = mX(x)].
Пример 4.5. Имеем нечеткое высказывание: ”На неделе было много прохладных дней”. Это высказывание можно формализовать и привести к конъюнктивной форме:<число дней есть близкое к 7 И температура воздуха есть невысокая>, где bX – число дней; aX- близкое к 7; bY - температура воздуха, aY - невысокая, bXопределяется на множестве X={3,5,6} в виде нечеткого множества СX ={<0,3/3>,<0,7/5>,<1/6>}, bY - на множестве Y ={10,15,20,25} в виде нечеткого множества СY = {<1/10>, <0,8/15>, <0,4/20>, <0,2/25>}.
Цилиндрические продолжения СX и СY будут равны:
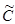 X = X =
| {<0,3/3,10)>,<0,3/(3,15)>,<0,3/(3,20)>,<0,3/(3,25)>,<0,7/(5,10)>, <0,7/(5,15)>, <0,7/(5,20)>, <0,7/(5,25)>, <1/(6,10)>, <1/(6,15)>, |
| <1/(6,20)>, <1/(6,25)>}; | |
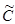 Y = Y =
| {<1/(3,10)>,<1/(5,10)>,<1/(6,10)>,<0,8/(3,15)>,<0,8/(5,15)>, <0,8/(6,15)>,<0,4/(3,20)>,<0,4/(5,20)>,<0,41/(6,20)>, <0,2/(3,25)>, <0,2/(5,25)>, <0,2/(6,25)>} . |
Тогда истинность высказывания: “На неделе было много прохладных дней”, приведенного в конъюнктивной форме (4.34), будет определяться на указанных множествах X и Y нечетким множеством
CÇ = 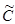 X Ç
X Ç 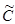 Y = {<0,3/(3,10)>, <0, 3/(3,15)>, <0,3/(3,20)>, <0,2/(3,25)>, <0,7/(5,10)>,<0,7/(5,15)>,<0,4/(5,20)>,<0,2/(5,25)>,<1/(6,10)>, <0,8/(6,15)>, <0,4/(6,20)>, <0,2/(6,25)>}.
Y = {<0,3/(3,10)>, <0, 3/(3,15)>, <0,3/(3,20)>, <0,2/(3,25)>, <0,7/(5,10)>,<0,7/(5,15)>,<0,4/(5,20)>,<0,2/(5,25)>,<1/(6,10)>, <0,8/(6,15)>, <0,4/(6,20)>, <0,2/(6,25)>}.
Очевидно, что наиболее истинным (v=1) приведенное высказывание будет при X=6 и Y=10, а наименее истинным (v =0,2) - при Y=25 и всех значениях X.
Следствием из правила (4.34) является преобразование
<bXесть aX1и aX2>®<(bX, bX) есть 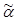 X1 Ç X1 Ç 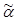 X2>. X2>.
| (4.35) |
Правило преобразования дизъюнктивной формы имеет вид:
<bX есть aXИЛИ by есть aY>®<(bX, bY) есть 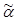 X È X È 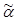 Y>, Y>,
| (4.36) |
где 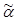 X È
X È 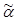 Y - значение лингвистической переменной (bX, bY) с соответствующим нечетким множеством
Y - значение лингвистической переменной (bX, bY) с соответствующим нечетким множеством
CÈ = 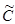 X È
X È 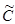 Y .
Y .
Это правило также имеет следствие
<bXесть aX1ИЛИ есть aX2>®<(bX, bX) есть 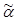 X1 È X1 È 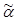 X2>. X2>.
| (4.37) |
Рассмотрим пример применения следствия.
Пример 4.6. Имеем высказывание: “Менее трудоспособными работниками являются дети и старики”, приведем данное высказывание к виду (4.37), где bX, лингвистическая переменная <нетрудоспособные работники> на множестве X = {10,15,20,25,30,50,60} со значениями aX1- <дети> и aX2- <cтарики>, выраженными нечеткими множествами
СX1= {<1/10>, <0,8/15>,<0,4/20>, <0,2/25>},
СX2= {<0,3/30>, <0,7/50>, <1/60>},
где X1 = {10,15,20,25}, X2 = {30,50,60}.
Получим
СÈ = 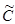 X1 È
X1 È 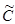 Y2 = {<1/(30,10)>, <0,8/(30,15)>, <0,4/(30,20)>, <0,3/(30,25)>, <1/(50,10)>,<0,8/(50,15)>,<0,7/(50,20)>,<0,7/(50,25)>,<1/(60,10)>, <1/60/15>, 1/(60,20)>, <1/(60,25)>}.
Y2 = {<1/(30,10)>, <0,8/(30,15)>, <0,4/(30,20)>, <0,3/(30,25)>, <1/(50,10)>,<0,8/(50,15)>,<0,7/(50,20)>,<0,7/(50,25)>,<1/(60,10)>, <1/60/15>, 1/(60,20)>, <1/(60,25)>}.
На основании полученного результата можно определить наиболее трудоспособные и наиболее нетрудоспособные бригады, состоящие из двух человек.
Правило преобразования импликативной формы имеет вид:
<ЕСЛИ bXесть aX ТО bY есть aY>®<(bX, bY) есть 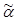 X à X à 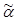 Y. Y.
| (4.38) |
Здесь знак à означает пороговую сумму, определяемую по выражению
("xÎX, "yÎY)[mà(x,y) = 1&(1-m 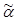 X(x,y)+m X(x,y)+m 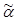 Y(x,y))], Y(x,y))],
| (4.39) |
где m 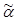 Xи m
Xи m 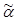 Y- функции принадлежности, определяющие нечеткие множества
Y- функции принадлежности, определяющие нечеткие множества  X È
X È 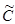 Y .
Y .
Пример 4.7. Представим высказывание: “Чем больше масса груза, тем на меньшее расстояние можно его перенести” в виде (4.38)
<ЕСЛИ (масса груза) есть (большой) ТО (расстояние есть (маленькое)>, где bX, - масса груза, bY- расстояние, aX- большой, aY- маленькое. Если взять все числовые данные из примера 4.5 для X и Y, СXи СY, то на основании выражения (4.39) получим функцию принадлежности mà(x,y) на мнoжестве X и Y.
mà(3,10) = 1& (1-0,3+1)=1,
mà(3,15) = 1&(1-0,3+0,8)=1,
mà(3,20) = 1&(1-0,3+0,4)=1,
mà(3,25) = 1&(1-0,3+0,2)=0,9,
mà(5,10) = 1&(1-0,7+1)=1,
mà(5,15) = 1&(1-0,7+0,8)=1,
mà(5,20) = 1&(1-0,7+0,4)=0,7,
mà(5,25) = 1&(1-0,7+0,2)=0,5,
mà(6,10) = 1&(1-1+1)=1,
mà(6,15) = 1&(1-1+0,8)=0,8,
mà(6,20) = 1&(1-1+0,4)=0,4,
mà(6,25) = 1&(1-1+0,2)=0,2.
Нечеткая переменная aX à aY будет характеризоваться нечетким множеством
Сà = 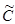 X à
X à 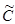 Y{<1/(3,10)>,<1/(3,.15)>,<1/1/(3,20)>,<0,9/(3,25)>, <1/(5,10)>, <1/(5,15)>,<0,7/(5,20)>,<0,5/(5,25)>,
Y{<1/(3,10)>,<1/(3,.15)>,<1/1/(3,20)>,<0,9/(3,25)>, <1/(5,10)>, <1/(5,15)>,<0,7/(5,20)>,<0,5/(5,25)>,  <1/(6,10), <0,8/(6,15)>, <0,4/(6,20)>, <0,2/(6,25)>}.
<1/(6,10), <0,8/(6,15)>, <0,4/(6,20)>, <0,2/(6,25)>}.
Рассмотрим еще одно, более сложное высказывание импликативной формы
| <ЕСЛИ bX, есть aX, ТО bYесть aY1, ИНАЧЕ bY есть aY2>. | (4.40) |
Это высказывание можно записать иным образом
<ЕСЛИ bX,есть aX,ТО bYесть aY1, И ЕСЛИ bX есть НЕaX ,ТО bYесть aY2>.
Тогда правило преобразования данной условной формы будет иметь вид
<ЕСЛИ bX, есть aX, ТО bY есть aY1, ИНАЧЕ aY2>®
®<(bX, bY) есть ( 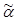 X à X à 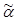 Y1)Ç Y1)Ç 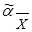 à à 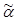 Y2)>. Y2)>.
| (4.41) |
Правило (4.41) является примером того, как можно использовать преобразования (4.34), (4.35),(4.36),(4.37), (4,38) для определения истинности сложных высказываний, основанных на высказываниях типа(4.24), (4.31), (4.32).
Существует правило, позволяющее использовать лингвистическую степень истинности при оценке истинности одних нечетких высказываний относительно других. Пусть имеются два высказывания: А:<b есть aА> и В: <b есть aB>, где aАи aB нечеткие переменные, определяемые нечеткими множествами СА и СВ на множестве X={x}. Тогда истинность А относительно В определяется как степень соответствия aАи aB посредством функции
| v(A,B) = v(A/B) = È mv(t)/t = {<mv(t)/t>}, | (4.42) | |||
| tÎ[0,1] | ||||
где "xÎX, t = mA(x), а mv(t) = sup mB(x), где X’{xÎX/t = mA(x)}.
| xÎ x’ |
Или иначе mv(t) = supmB(x)/t= mA(x).
Здесь mAи mB- функции принадлежности нечетких переменных aАи aB; mv(t)- функция принадлежности значения истинности, tÎ[0;1] - область ее определения.
Правило (4.42) утверждает, что истинностью нечеткого высказывания А относительно нечеткого высказывания В является нечеткое множество v(A,B), определенное на интервале [0;1], такое, что для любого tÎ[0;1] значение ее функции принадлежности равно наибольшему значению mB(x) по всем x, при которых mA(x)=t.
Пример 4.8. Имеем два высказывания:
А: <b находится близко к 5>,
В: <b имеет значение приблизительно 6>.
Тогда aАº <близко к 5> и aB º <приблизительно 6> - это нечеткие переменные с нечеткими множествами:
СА={<0,1/2>,<0,3/3>,<0,7/4>,<1/5>, <0,8/6>, <0,6/7>, <0,3/8>, <0,1/9>},
CB={<0,1/3>,<0,4/4>,<0,8/5>,<1/6>, <0,7/7>, <0,4/8>, <0,3/9>,<0,1/10>}.
Истинность высказывания В относительно высказывания А на множестве X={2,3,4,5,6,7,8,9,10} будет
v(B/A)={<0,1/0>,<0,3/0,1>,<0,4/0,3>,<0,7/0,6>,<0,4/0,7>,<1/0,8>,<0,8/1>}.
Cуть правила (4.42) хорошо иллюстрируется двумя следствиями, вытекающими из него.
Следствие 1. Пусть А:<b есть x1> - четкое высказывание. В этом случае значение x1 можно рассматривать как нечеткую переменную ax1, характеризуемую нечетким множеством Сx1 = {<mx1(x)/x>} с функцией принадлежности
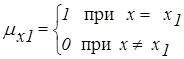 .
.
Если имеется нечеткое высказывание В:<b есть aB>, тогда истинность высказывания А относительно нечеткого высказывания В полностью определяется одним значением mB(x1)
| V(A/B) = {<mB(x1)/1>}. | (4.43) |
Cтепень истинности V(A/B) фактически отражает объективность оценки вполне конкретной ситуации А нечетким высказыванием В того или иного эксперта.
Пример 4.9. Пусть А:<b есть 5> - четкое высказывание суть ситуации, а описание ситуации нечеткое В: <b есть приблизительно 6>. В таком случае (см. пр.4.8) СА={<1/5>}, а СВ={<0,8/5>}. Тогда v(A/B) = {<0,8/1>}, т.е. истинность высказывания В по отношению к конкретной ситуации (когда А абсолютная истина, т.е. v(A)=1 равна 0,8.
Следствие 2. Пусть А: <b есть x1> и B:< b есть x2> - четкие высказывания. Тогда истинность одного четкого высказывания относительно другого четкого высказывания будет
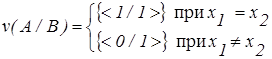 ,
,
что вполне естественно.
Дата добавления: 2021-10-28; просмотров: 435;











