Метод построения функции принадлежности лингвистических термов с использованием статистических данных
В процессе наблюдения за объектом в течение некоторого времени человек n - раз фиксирует свое внимание на том, имеет место факт А или нет. Событие, заключающееся в k проверках наличия факта А называется оценочным. Пусть в k проверках имеет место факт А, тогда частота его появления определяется как р=k/n. Оценивая частоту проявления р, человек опирается на свой опыт, который отражает частоту появления факта А в событиях прошлого. Имеет место поступающая также информация, отражающая общественный опыт, основанная на наблюдениях людей для изучения появления факта А. В зависимости от степени доверия к источнику такого рода информация запоминается с различными весами. Например, предположим, что эксперту предлагается оценить в лингвистической переменной «относительная величина» значение отклонения ΔB (отклонение параметра технологического процесса, где B - максимально возможное отклонение и характерно выполнение условия 0<ΔB/B<1). Обозначим терм множества, составляющие лингвистическую переменную, как: «очень мало», «мало», «средне», «много», «очень много».
Интервал изменений ΔB/B разделится на несколько отрезков, допустим 20. Далее осуществляется сбор статистики, характеризующей, на сколько часто человек употребляет слова для выражения своего представления о значении ΔB/B, результаты которого представлены в табл.3.6.
Таблица 3.6. Статистика результатов экспертного опроса
| Терм-множества | ||||||||||||||||||||
| «очень мало» | ||||||||||||||||||||
| «мало» | ||||||||||||||||||||
| «средне» | ||||||||||||||||||||
| «много» | ||||||||||||||||||||
| «очень много» | ||||||||||||||||||||
| ki |
Используя свойство функции принадлежности необходимо предварительно обработать данные таким образом, чтобы уменьшить искажения вносимые экспериментом.
Естественными свойствами функции принадлежности являются: наличие одного максимума и гладкие затухающие до нуля факты. Для обработки статистических данных можно воспользоваться матрицей подсказок. Предварительно из таблицы удаляются явно ошибочные элементы, критерием удаления которых служит наличие нескольких нулей в строке вокруг рассматриваемого элемента. Элементы матрицы вычисляются по формуле (3.32).
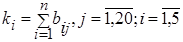
| (3.32) |
В строке выбирают максимальный элемент kmax и все элементы данной таблицы преобразуются по формуле (3.33)
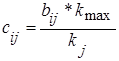
| (3.33) |
Если kj = 0, применяется линейная аппроксимация: 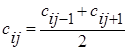 .
.
Таблица 3.7. Нормированные результаты экспертного опроса
| j | i | |||||||||||||||||||
| 7,5 | 4,75 | |||||||||||||||||||
| 2,5 | 5,25 | 6,6 | 3,3 | |||||||||||||||||
| 3,3 | 6,6 | |||||||||||||||||||
| 8,3 | 3,75 | |||||||||||||||||||
| 1,6 | 6,25 |
Завершающим этапом является определение функции принадлежности, используя формулу нормализации (3.34).
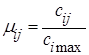
| (3.34) |
m11 = 1; m12 = 1; m13 = 0,75; m14 = 0,475; m15 = 0,2; остальные нули.
Аналогичным образом осуществляются расчеты для остальных терм-множеств лингвистической переменной «относительна величина».
Функция принадлежности, полученная в результате всех вычислений предствлена на рис.3.19.

Рис.3.19. Терм-множенство «очень мало» лингвистической переменной
«относительная величина»
Дата добавления: 2021-10-28; просмотров: 458;











