Нечеткая и лингвистическая переменные
Понятие переменной является основополагающим математическим понятием. В практических приложениях теории нечетких множеств обычно употребляют нечеткие и лингвистические переменные.
Нечеткие и лингвистические переменные используются при естественно-языковом описании различных объектов и явлений, при формализации процессов принятия решений в трудноформализуемых ситуациях, в описании сложных явлений.
Способность человека оценивать информацию играет существенную роль в определении сложных явлений. По своей природе оценка является приближением. Во многих случаях, достаточна весьма приближенная характеристика набора данных, поскольку в большинстве задач, решаемых человеком, не требуется высокая точность.
Способность человека оценивать информацию наиболее ярко проявляется в использовании естественных языков. Каждое слово x можно рассматривать как сжатое описание нечеткого подмножестваA(x) полного множества области рассуждений X. Таким образом, A(x) есть значение x. В этом смысле весь язык можно рассматривать как систему, в соответствии с которой нечетким подмножествам множества Х приписываются элементарные или составные символы, т.е. слова, группы слов и предложения.
Так, например, если значение существительного шар есть нечеткое подмножество А(шар), а значение прилагательного красный - нечеткое подмножество А(красный), то значение сочетания красный шар является пересечением А(шар) и А(красный).
Если рассматривать цвет объекта как некоторую переменную, то ее значения: красный, синий, зеленый и т.д. можно интерпретировать как символы нечетких подмножеств полного множества. В этом смысле определенный цвет предмета является нечеткой переменной, т.е. переменной значениями которой являются символы нечетких множеств.
Нечеткой переменной н а з ы в а е т с я
< a, Х, Сa >,
где a - наименование нечеткой переменной; Х={x} - область ее определения (базовое множество); Сa - {<mА(x) / x>} - нечеткое множество на Х, описывающее ограниченные, но возможные значения нечеткой переменной a.
Пример 2.13. Предположим, что Х={1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Тогда нечеткое подмножество, описываемое понятием несколько, можно записать, например, в виде:
несколько = 0,5/3 + 0,8/4 + 1/5 + 1/6 + 0,8/7 + 0,5/8 или
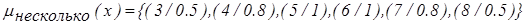
Аналогично, если Х - интервал [0, 100] с элементами переменной возраст, то нечеткие подмножества, описываемые понятиями "молодой" и "старый", можно представить в виде функций принадлежностей:
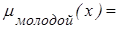 {(1/5), (1/10), (1/15), (1/20), (1/25), (0.5/30), (0.2/35), (0.1/40), (0.05/45), (0.03/50), (0.02/55)};
{(1/5), (1/10), (1/15), (1/20), (1/25), (0.5/30), (0.2/35), (0.1/40), (0.05/45), (0.03/50), (0.02/55)};
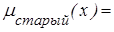 {(0/30), (0/35), (0/40), (0/45), (0/50), (0.5/55), (0.8/60), (0.9/65), (0.95/70), (1/75)}.
{(0/30), (0/35), (0/40), (0/45), (0/50), (0.5/55), (0.8/60), (0.9/65), (0.95/70), (1/75)}.

Рис.2.16. Графическое представление нечеткой переменной «возраст».
Подробно вопрос построения функции принадлежности нечеткой переменной будет рассмотрен в п. 3.7.
В более общем случае значениями таких переменных могут быть слова или предложения естественного или формального языка, и тогда соответствующие переменные называют лингвистическими. Так, например, нечеткая переменная высота могла бы принимать следующие значения: высокий, невысокий, довольно высокий, очень высокий, высокий, но не очень, вполне высокий, более или менее высокий. Эти значения представляют собой предложения, образованные понятием высокий, отрицанием не, союзами и, но, а также словами типа очень, довольно, вполне, более или менее.
Лингвистическая переменная является переменной более высокого порядка, чем нечеткая переменная, в том смысле, что значениями лингвистической переменной являются нечеткие переменные. Лингвистические переменные предназначены в основном для анализа сложных или плохо определенных явлений. Использование словесных описаний типа тех, которыми оперирует человек, делает возможным анализ систем настолько сложных, что они недоступны обычному математическому анализу.
Лингвистической переменной н а з ы в а е т с я
< b, Tb,, Х, G, M>,
где b - наименование лингвистической переменной; Tb - множество ее значений (терм-множество), представляющих собой наименования нечетких переменных, областью определения (базовым множеством) каждой из которых является Х; G - синтаксическое правило, порождающее наименование a Î Tb вербальных значений лингвистической переменной b; М - семантическое правило, ставящее в соответствии каждой нечеткой переменной a Î Tb, нечеткое множество Сa, т.е. смысл (семантику) нечеткой переменной a. В более упрощенном виде лингвистическая переменная описывается кортежем < Tb ,b , Х>.Это возникает в тех случаях, когда лингвистическая переменная имеет определенный характер, т.е. терм-множество и описывающие термы нечеткие переменные носят установившиеся значения. Однако в той или иной ситуации может оказаться, что установленных термов, т.е. числа вербальных значений лингвистической переменной в зоне базового множества недостаточно (или, наоборот, избыток). В этом случае по определенному правилу G добавляются (исключаются) другие термы, а по правилу М им (а иногда и оставшимся термам) ставится в соответствии нечеткая переменная. В этом случае Tb называют базовым терм - множеством, а Tb* =Tb È G(T) - расширенным терм - множеством лингвистической переменной.
Процедура образования новых термов G осуществляется с помощью логических связок Не, И и ИЛИ и модификаторов типа «очень», «слегка». Процедура задания нечетких переменных М, например, 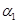 = «малая скорость»,
= «малая скорость», 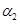 = «средняя скорость»,
= «средняя скорость», 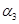 = «высокая скорость», а так же соответствующих нечетких множеств для термов из
= «высокая скорость», а так же соответствующих нечетких множеств для термов из 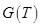 выполняется в соответствии с правилами трансляции нечетких связок и модификаторов. Правило М может быть выполнено по одной из типовых операций над нечеткими множествами, которые рассмотрены в п.2.2.
выполняется в соответствии с правилами трансляции нечетких связок и модификаторов. Правило М может быть выполнено по одной из типовых операций над нечеткими множествами, которые рассмотрены в п.2.2.
Пример 2.14. Стоимость необходимого товара оценивается с помощью понятий “низкая”, “средняя”, “высокая”. В рыночных ценах эта стоимость изменяется от 12000 до 15000 руб. Формализуем данное описание введением лингвистической переменной <“Стоимость”, Tb , [12000, 15000]> где Tb = {“низкая”, “средняя”, “высокая”} значения лингвистической переменной “Стоимость” из терм-множества Tb описываются нечеткими переменными с соответствующими наименованиями (“низкая”, “средняя”, “высокая”) и ограничениями [12000, 15000] на возможные значения:
- значение “низкая” задается нечеткой переменной <“низкая”, [12000, 15000],См>, где нечеткое множество
См{<1/12000>,<0,8/12500>,<0,5/13000>,<0,2/13500>,<0,05/14000>, <0/15000>}; - значение “средняя” задается нечеткой переменной <“средняя”, [12000, 15000], Cc>,
Cc= {<0/12000>, <0,2/12500>, <0,6/13000>, <1/13500>, <0,8/14000>,
<0,3/14500>, <0/15000>};
- значение “высокая” задается нечеткой переменной <“высокая”, [12000, 15000], Св>}; Cв={<0/12000>, <0/12500>, <0/13000>, <0,3/13500>, <0,7/14000>, <1/14500>, <1/15000>}.
Функции принадлежностей, описывающие терм множества, представлены на рис.2.17.
 mсa
mсa
“низкая” “средняя” “высокая”
0,8
0,6
0,4
0,2
12000 13000 14000 15000 Х руб.
Рис.2.17. Графическое изображение лингвистической переменной
Синтаксические правила G, порождают новые термы с использованием модификаторов "очень" и "более-менее" и логической связки "не". Семантические правила M, описывающие нечеткие переменные «очень низкая», «не высокая», «более-менее средняя», и определяемые по формулам (2.16), (2.13,), (2.17) соответственно, представим в виде табл.2.4.
Таблица 2.4. Образование новых термов лингвистической переменной «стоимость»
| Терм множество | Синтаксическое правило | Семантическое правило |
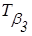 («высокая») («высокая»)
| не 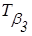
| 1- 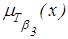
|
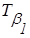 («низкая») («низкая»)
| очень 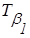
| 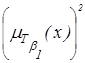
|
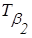 («средняя») («средняя»)
| более-менее 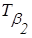
| 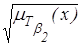
|
Графики функций принадлежностей новых термов лингвистической переменной «стоимость» показаны на рис.2.18.
 mсa
mсa
“низкая” “средняя” “высокая”
0,8
0,6
0,4
0,2
12000 13000 14000 15000 Х руб.
Рис.2.18. Функции принадлежностей новых термов лингвистической переменной
Язык можно рассматривать как соответствие между множеством терминов Тb и областью рассуждения Х. Это соответствие характеризуетсянечетким называющим отношением b из Тb в Х, которое связывает с каждым терминомTi в Тb и каждым элементом х в Х степень mb (Ti, x) применимости Ti к х.
Для фиксированного Ti функция принадлежности mb (Ti, x) определяет нечеткое подмножество М(Ti) из Х, которое является смыслом или значением Ti. Таким образом, значение терминаTi есть нечеткое подмножество М(Ti) из Х, для которого Ti служит символом.
Термин может быть элементарным, например Ti = высокий, или составным, когда он является сочетанием элементарных терминов, например, Ti = очень высокий.
Более сложные понятия могут характеризоваться составной лингвистической переменной. Для лингвистической переменной возраст соответствующая базовая переменная является по своей природе числовой переменной. С другой стороны, для лингвистической переменной внешность мы не имеем четко определенной базовой переменной. В этом случае функцию принадлежности определяют не на множестве математически точно определенных объектов, а на множестве обозначенных некими символами.
Лингвистические переменные играют важную роль при построении нечетких моделей: с их помощью формализуется качественная информация об объекте принятия решения, представленная в словесной (или вербальной) форме специалистами-экспертами, т.е. лингвистические переменные и их значения (нечеткие переменные) служат для качественного, словесного описания количественных величин. Поэтому принципиально важным является то, что любая лингвистическая переменная, как и все ее значения, определяется конкретной количественной шкалой, называемой базовой шкалой Х). Отсюда вытекает другое определение лингвистической переменной. Лингвистической называется переменная, заданная на некоторой шкале (базовой шкале) и принимающая значения, являющиеся словами и словосочетаниями естественного языка. Значения лингвистической переменной описываются нечеткими переменными.
А. Борисов и др. сформулировали ряд условий, которым в силу своей семантики должны удовлетворять функции принадлежности нечетких множеств, термы лингвистических переменных.
Пусть Tb={Ti}(iÎ L={1,2,...,m}) базовое терм-множество лингвистической переменной <b, Tb , X>; <Ti , Х, Сi> - нечеткая переменная, соответствующая терму TiÎ Tb; Сi={<mci(x) / x >}, xÎ X: при этом Sci - носитель нечеткого множества Сi . Допустим, что X Í R, где R - действительная ось. Обозначим inf X через х1, а sup X через х2. Упорядочим базовое терм-множество Tb в соответствии с выражением:
| ("Ti Î Tb) ("Tj ÎTb) (i>j)«($ xÎ Sci) ("yÎ Sci)(x>y), | (2.44) |
означающим, что терм, который имеет носитель, расположенный левее, получает меньший номер. Тогда терм-множество любой лингвистической переменной b должно удовлетворять следующим условиям:
| mc1(х1)=1, mcm (х2)=1, | (2.45) |
| (" Ti Î Tb ) (0 < sup mci Ç ci+1 (x)<1) , | (2.46) |
| (" Ti Î Tb) ($ xÎ X) (mci(х) = 1) , | (2.47) |
| ("b) ($ х1Î R) ($ х2Î R) (("xÎ X) (х1< x< х2)) . | (2.48) |
Указанные условия прокомментируем на примере.
Пример 2.15. Представим лингвистическую переменную b с числом термов равным пяти (рис.2.19).
Условие (2.45) представляет единственно возможным вид амодальности функциям принадлежности крайних термов, что обусловлено расположением этих термов в упорядоченном множестве Tb. Правильное представление крайних термов можно отметить на рис.2.19.
Условие (2.46) запрещает существование в базовом терм-множестве Tbпар термов типа Т1и Т2, а также Т2 и Т3, поскольку в первом случае отсутствует естественная ограниченность понятий, аппроксимируемых термами, а во втором случае участку [a; b]Î Х не соответствует никакое понятие. Поскольку каждое понятие, т.е. лингвистическое значение, обозначенное термом, имеет хотя бы один типичный объект из множества объектов описываемый данной лингвистической переменной, введено условие (2.47), запрещающее наличие во множестве Тb термов типа Т4, имеющих supmс1(х)<1.
 mсi
mсi
Т1Т2 Т3 Т5 Т4
X
а b
Рис.2.19. Лингвистическая переменная с некорректным определением термов
Аналогичный запрет относится и к термам, имеющим supmс1(х)>1, т.е. термы должны описываться нормированными функциями принадлежности. Условие (2.48) ограничивает область определения Х конечным множеством точек. Это условие констатирует имеющиеся в любой задаче анализа и принятия решения реальные ограничения на числовые значения параметров объекта.
В общем случае значение лингвистической переменной есть составной терм T=t1t2…tn, который представляет собой сочетание элементарных термов t1t2…tn. Эти элементарные термы можно разбить на 4 категории:
1. Первичные термы, которые являются символами нечетких подмножеств области рассуждения (например, “молодой”, “старый”);
2. Отрицание “не” и союзы “и”, “или”;
3. Лингвистические неопределенности типа “очень”, “много”, “слабо”, “более или менее” и т.д., которые дают возможность модифицировать значения элементарных и составных терминов и служат для увеличения области значений лингвистической переменной;
4. Маркеры, такие, как скобки, вводные слова.
Основная проблема, которая возникает в связи с использованием лингвистических переменных, заключается в следующем: пусть дано значение каждого элементарного термина в составном терме T=t1t2…tn, требуется вычислить значение T, т.е. найти нечеткое множество вХ, символом которого является термT.
Рассмотрим вначале вычисление значения составного терма в виде Т= hu, где h - неопределенность, аu - терм с фиксированным значением, например, h = очень, а u = “высокий”.
Неопределенности выполняют функцию генерации большого множества значений для лингвистической переменной из небольшого набора первичных терминов. Поэтому неопределенность h можно рассматривать как нелинейный оператор, который переводит нечеткое множествоМ(u), представляющее значение u, в нечеткое множество М(hu) и таким образом преобразует смысл соответствующих термов.
Хотя в повседневном использовании неопределенность очень не имеет четко определенного значения, в сущности, она действует как усилитель, генерируя подмножество того множества, к которому она применяется.
При вычислении значения составного терма используются обычные правила предшествования, действующие при преобразовании булевских выражений. С добавлением неопределенностей эти правила выражаются следующим образом:
1. h, не,
2. и,
3. или.
Для изменения порядка предшествования можно использовать скобки.
Рассматриваемый подход можно применять к вычислению значений лингвистической переменной, при условии, что составные термы, представляющие эти значения, могут быть генерированы лишенной контекста грамматикой.
Чтобы вычислить значения составного терма Т, необходимо провести синтаксический анализ Т в терминах определенной грамматики. Тогда, зная синтаксическое дерево Т, можно использовать соотношения, порождаемые правилами вывода, для составления системы уравнений, решением которой является значениеТ.
В общем случае число элементов множества Т может быть бесконечным, и тогда как для порождения элементов множества Т, так и для вычисления их смысла необходимо применять некоторый алгоритм. Говорят, что лингвистическая переменная N структурирована, если ее терм-множество Т и функцию М, которая ставит в соответствие каждому элементу терм-множества его смысл, можно задать алгоритмически.
В качестве простого примера рассмотрим лингвистическую переменную Возраст. Допустим, что терм-множество этой переменной можно записать в виде:
Т(Возраст) = старый + очень старый + очень очень старый + ...
В этом случае каждый терм множества Т имеет вид старый или очень ... очень старый.Чтобы вывести это правило в более общем виде, можно рассматривать данное представление для Т(Возраст) как решение уравнения
Т = старый + очень Т, которое означает, что множество Тсостоит из терма старый и термов, состоящих из слова очень и некоторого терма изТ.
Данное уравнение можно решать итеративным способом, используя рекуррентное соотношение
Тi+1 = старый + очень Тi, i = 0,1,2,...
Взяв пустое множество Æ в качестве начального значения, получаем
Т0 =Æ,
Т1 = старый,
Т2 = старый + очень старый,
Т3= старый + очень старый + очень очень старый,
. . .
Т.е. решение уравнения (Т = старый + очень Т) имеет вид
Т = старый + очень старый + очень очень старый + ...
Более общий подход базируется на определении семантики контекстно-свободных языков. Например, можно проверить, что терм-множество порождается контекстно-свободной грамматикой G=(VT,VN,T,P), в которой нетерминальные символы (синтаксические категории) обозначаются VN = T + A + B + C + D + E, в то время как множество терминальных символов (компоненты термов в Т) выражаются в виде VT = молодой + старый + очень + не + и + или + ( ), а систему P можно представить алгебраически в виде следующей системы уравнений:
Т = A + Т или A,
A = B + A и B,
B = C + не С,
C = (T) + D + E,
D = очень D + молодой,
E = очень E + старый.
Итерирование порождает все больше и больше термов в каждой из синтаксических категорий (T, A, B, C, D, E).
В более общепринятой процедуре терм в Т, скажем, не молодой и не старый порождается грамматикой G путем последовательных замен (подстановок) с использованием системы P, причем каждая цепочка подстановок начинается с Т. Цепочку можно получить, используя синтаксическое дерево (рис.2.18), представляющее структуру терма не молодой и не старый с использованием синтаксических категорий T,A,B,C,D,E. Описанная процедура порождения термов в Т грамматикой G в сущности составляет синтаксическое правило для переменной Возраст.
Семантическое правило для переменной Возраст индуцируется описанным выше синтаксическим правилом, так как смысл терма в Т частично определяется его синтаксическим деревом.
В частности, каждому правилу подстановки ставится в соответствие некоторое отношение между нечеткими множествами, обозначенные определенными терминальными и нетерминальными символами. Эта двойственная система подстановок и связанных с ней уравнений используется для вычисления смысла составных термов из Т как представлено на рис.2.20.
1. Рассматриваемый терм подвергается грамматическому разбору, в результате чего получается синтаксическое дерево. Конечными вершинами этого дерева являются:
а) первичные термы, смысл которых определяется априори,
б) названия модификаторов (т.е. лингвистических неопределенностей, союзов, отрицания и т.п.),
в) маркеры, такие, как скобки, которые облегчают грамматический разбор.
2. Первичным термам на конечных вершинах дерева назначается их смысл и затем с помощью системы подстановок Р и соответствующих уравнений вычисляется смысл ближайших к ним нетерминальных символов.
3. После этого дерево урезают так, чтобы вычисленные терминальные символы оказались конечными вершинами оставшегося поддерева.
Этот процесс повторяется до тех пор, пока не будет вычислен смысл терма, соответствующего корню исходного синтаксического дерева. Основное назначение описанной процедуры состоит в том, чтобы связать смысл составного терма со смыслом составляющих его первичных термов посредством системы уравнений, определяемой грамматикой, порождающей термы вТ.

Рис.2.20. Синтаксическое дерево для значения “немолодой” и “нестарый”
Рассмотрев одно из основных математических понятий - переменную с позиции теории нечетких множеств - можно еще раз констатировать, что в этой теории определяющая роль отводится понятиям “степень принадлежности” и “функция принадлежности” (аналогично тому, как в теории вероятности - понятие “вероятность” и “функция распределения вероятностей”). В то же время основной трудностью, мешающей интенсивному применению теории нечетких множеств при решении практических задач, является то, что степени принадлежности, функции принадлежности задаются как бы вне самой теории. В связи с этим в каждом методе построения функции принадлежности формулируются свои требования и обоснования к выбору именно такого построения.
Контрольные вопросы
1. Какие множества (подмножества) называют нечеткими?
2. Как определяется принадлежность элементов нечеткому множеству?
3. Как определяется связь нечеткого множества с обычными теоретико-множественными представлениями?
4. Что означают нечеткие отношения? Как они описываются?
5. Какова роль функции отображения в формировании нечетких множеств?
6. Как можно использовать теоретико-множественные операции для формирования нечетких множеств?
7. Как определяются меры сходства и различия нечетких множеств?
8. Что подразумевается под понятием индекс нечеткости?
9. Каково практическое применение мер сходства, различия и размытости нечетких множеств?
10. Как осуществляется описание нечеткой и лингвистической переменной?
11. Какие правила (условия) формирования лингвистической переменной?
12. Где и в каких случаях используются нечеткие и лингвистические переменные?
Дата добавления: 2021-10-28; просмотров: 638;











