Глава 3. МЕТОДЫ ПОСТРОЕНИЯ ФУНКЦИИ ПРИНАДЛЕЖНОСТИ

Содержание функции принадлежности

Прежде чем остановиться на конкретном рассмотрении известных методов построения функций принадлежности, отметим некоторое толкование сущности этих функций, а также обозначим основные направления, связанные с различными толкованиями и вытекающими из этого подходами к определению степени принадлежности и построению функции принадлежности.

Существует несколько точек зрения на содержательную интерпретацию функций принадлежности, при которых преобладающей оценкой степени принадлежности является фиксирование конкретных значений в интервале [0,1]. Такое фиксирование носит субъективный характер и производится в результате экспертного опроса.

Для методов, основанных на экспертных оценках, важным является характер измерений: первичный, т.е. непосредственный, или производный, т.е. косвенный, а также тип шкалы, которой пользуется эксперт и которая затем определяет вид операций по обработке экспертной информации. Другой особенностью можно назвать то, что оцениваемые объекты обладают двумя типами свойств:

1) свойства, которые можно непосредственно измерить, например: длину, высоту, рост, вес, объем и т.п.,

2) свойства, которые не имеют количественной меры, а являются качественными, например: красота, удобство, полезность и т.п.

Во втором случае, как правило, прибегают к попарному сравнению объектов, обладающих качественными свойствами и определяющих место (ранг) по отношению к рассматриваемому понятию А.

В некоторых работах на основании формального определения функции принадлежности и операции дополнения нечеткого множества дается следующая интерпретация: величина m_А(х) есть условная вероятность наблюдения события А при наблюдении х. При этом предпочтение отдается субъективной вероятности, суть которой заключается в следующем. Пусть х – некоторое событие реального мира, а А_х – некоторое другое событие, которое дает некоторый выигрыш Q₁, если х произойдет, и Q₂, если х не произойдет. Имеется также событие А_р, которое дает выигрыш Q₁с объективной, в частности, частотной вероятностью р, и выигрыш Q₂- с вероятностью (1-р). В этом случае величина р называется субъективной вероятностью события х при условии, что субъекту безразлично, какое из событий А_х или А_р произойдет. Значение вероятности при этом понимается как число, пропорциональное сумме, которую субъект согласен заплатить в том случае, если высказывание, являющееся по его утверждению истинным, в действительности окажется ложным. В большинстве известных работ по исследованию и применению нечетких множеств считается, что функция принадлежности - это некоторое невероятностное субъективное измерение нечеткости и что она отличается от вероятностной меры и интерпретируется как субъективная мера того, насколько элемент (событие) хÎ Х соответствует понятию А.

При этом степень соответствия оценивается не вероятностной, а возможностной мерой, т.е. не условной вероятностью наблюдения события А при возникновение события х, а возможностью (или необходимостью) интерпретации х событием А.

Существующие методы построения функции принадлежности можно разделить на группы: прямые и косвенные.

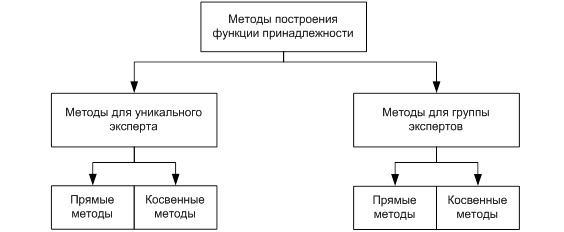
Рис.3.1. Классификация методов построения функции принадлежности

Прямые методы заключаются в том, что эксперт непосредственно задает степень принадлежности каждого хÎ Х понятию А или определяет вид функции m_А(х). При этом значения функции согласуются с предпочтениями эксперта по отношению х_i на множестве Х следующим образом:

- для любых х₁, х₂Î Х m_А(х₁)<m_А(х₂) тогда и только тогда, когда х₂ предпочтительнее х₁ т.е. в большей степени (с большей вероятностью, с большей возможностью, с большей необходимостью) характеризуется понятием А;

- для любых х₁, х₂Î Х m_А(х₁)=m_А(х₁) тогда и только тогда, когда х₁и х₂безразличны относительно понятия А.

Как правило, прямые методы используются для описания объектов, свойства которых можно непосредственно измерить. В этом случае осуществляют непосредственное задание значений степени принадлежности. К прямым методам можно отнести методы, основанные на вероятностной трактовке функции принадлежности m_А(х) = р(x/A), т.е. вероятность того, что объект хÎ Х будет отнесен к нечеткому множеству А.

При использовании вероятностной меры в прямых методах была обнаружена субъективная тенденция сдвигать оценки объектов в направлении концов оценочной шкалы. Эта тенденция может быть объяснена выражением (1.23), в связи с чем предлагается непосредственное определение принадлежности осуществлять по возможностной мере

В косвенных методах значения функции принадлежности выбираются исходя из заранее сформулированных условий. Информация, поступающая от экспертов, является лишь исходной для реализации установленного в данном методе алгоритма обработки этой информации в целях получения m_А(х). Косвенные методы являются единственно возможными в тех случаях, когда свойства, через которые определяется понятие А, не имеют количественной меры, например, “красота”. В таких случаях используют ранговые измерения при попарном сравнении объектов. Косвенные методы более трудоемки, чем прямые, но их преимущество - в стойкости по отношению к искажениям в ответе, а следовательно, в большей объективности получаемой функции принадлежности.

В целях повышения объективности функции принадлежности для ее построения учитывают мнение как одного (индивидуального) эксперта, так и группы экспертов. Групповая процедура построения функции принадлежности используется как в прямых, так и в косвенных методах.