Построение функции принадлежности нечеткого множества и оценка его вероятностных характеристик

Рассмотрим вероятностные критерий достоверности и метод построения функции принадлежности. Предлагаемый метод в сочетании с известными методами теории возможности позволяет получить оценку для вероятности, совпадающую с оценкой, получаемой методами теории возможности.

Рассмотрим следующую цепочку операций, схематически представленную на рис.3.2:

- По известным плотностям вероятности случайных величин строятся функции принадлежности соответствующих нечетких величин;

- Находятся значения некоторых функций от полученных нечетких и исходных (случайных) величин;

- Сравниваются результаты, и оценивается плотность распределения вероятности полученной случайной величины с помощью распределения возможности нечеткой величины;

Если при этом будет установлена связь между возможностью и вероятностью, можно будет расширить теорию возможности мощными и признанными (что в некоторых случаях играет чрезвычайно важную роль) методами теории вероятности.

Для работы с нечеткими множествами необходимо построить функцию принадлежности.

Пусть для рассматриваемой случайной величины X_p, характеризующейся плотностью вероятности p_Х (х), соответствующая ей нечеткая величина обозначается X_m­, а ее функция возможности µ_Х(х)(рис.3.2).

Введем обозначение того, что величина A характеризуется функцией a_A(x): A ~ a_А. Используя данное обозначение, можно записать, что X_ρ ~ p_X и X_µ ~ µ_X . Несмотря на то, что нечеткие и вероятностные величины имеют несколько разную природу, “понятия плотности вероятности и функции принадлежности сравнимы”.

Рис.3.2. Связь вероятности и возможности

Пусть для случайной величины X_p нам известна плотность распределения вероятности: X _p~ p_X(х). Она может быть задана априори или получена статисти­чески. Построим для данной случайной величины функцию принадлежности следующим образом:

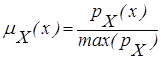,	(3.1)
где .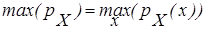

Эта функция отвечает интуитивным представлениям о том, что достоверность более вероятного события выше, чем достоверность менее вероятного события.

Кроме того, построенная функция обладает следующими свойствами:

мin(m_X(x)) ≥0,

max(m_X(x)) =1.

Построенная нами функция является функцией принадлежности нормального нечеткого множества. Несмотря на то, что такой метод определения функции принадлежности является допустимым с точки зрения теории возможностей, было бы неплохо получить аналогичный результат другим способом, например, воспользовавшись методом экспертных оценок.

Пусть при изучении некоторой случайной величины была построена гистограмма распределения вероятности, представленная на рис.3.3.

Рис.3.3. Гистограмма распределения случайной величины

Здесь N_i- количество точек, принадлежащих интервалу [x_i-1, x_i];

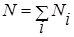- количество точек, образующих гистограмму;

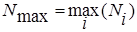- количество точек, принадлежащих интервалу[x_i-1, x_i];.

Пусть известно, что данное распределение имеет плотность вероятности ρ_X(x), тогда при росте количества точек, образующих гистограмму, величина 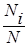будетстремиться к p_X(x_i). Можно показать, что при этом отношение 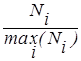будет стремиться к .

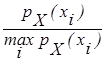Пусть у нас есть M экспертов, будем предъявлять им каждую частоту в гистограмме и задавать им вопрос: можно ли считать достоверным, что случайная переменная примет значение, характеризующиеся такой частотой в гистограмме. От эксперта ожидается однозначный (булевый) ответ. В результате для каждой частоты гистограммы и для каждого эксперта можно получить функцию достоверности γ(m,N_i):

,

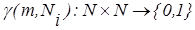где γ(m,N_i) принимает значение 1, если с точки зрения m-ого эксперта (mÎ[0,M-1]) значение, характеризующиеся частотой N_i является достоверным, 0 – если недостоверным.

Пусть m-ый эксперт (mÎ[0,M-1]) считает, что значение с частотой N_i достоверно, если 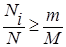. Таким образом, получен набор мнений экспертов, различающихся степенью пессимистичности.

Определим функцию принадлежности для xÎ[x_i;x_i+1) как,

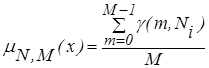
(3.2)

Преобразуем (3.2) воспользовавшись критерием :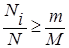

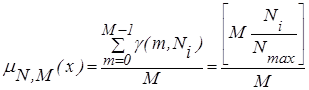
(3.3)

Можно показать, что при росте числа экспертов и количества точек гистограммы функция µ_{M, N} (x), (3.3) стремится к функции 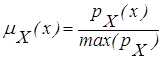, совпадающей с формулой (3.1).

Отметим один принципиальный вопрос, возникающий в связи с изложенными подходами к построению функции принадлежности: в качестве недостатка вероятностного подхода отмечалась сложность определения распределений вероятностей. После этого все построения строились на том, что известна плотность вероятности. Для разрешения данного логического противоречия сделаем следующее допущение. Пусть неизвестна плотность вероятности ρ_Х(x), но мы можем оценить ее сверху функцией 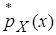: p_Х(x)£ .

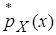По формуле (3.1) получим функцию принадлежности:

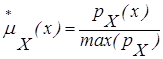
(3.9)

Таким образом, возможно, оценив функцию плотности вероятности и перейдя к нечетким переменным, работать с данными с помощью аппарата нечетких множеств.