Основные идеи алгоритма для решения сформулированной задачи нечеткой кластеризации были предложены Д. К. Данном.
Алгоритм имеет итеративный характер последовательного улучшения некоторого исходного нечеткого разбиения 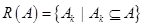 , которое задается пользователем или формируется автоматически по некоторому эвристическому правилу.
, которое задается пользователем или формируется автоматически по некоторому эвристическому правилу.
На каждой из итераций рекуррентно пересчитываются значения функций принадлежности нечетких кластеров и их центры.
Алгоритм заканчивает свою работу, если произойдет выполнение заранее заданного числа итераций или когда минимальная абсолютная разность между значениями функций принадлежности на двух последовательных итерациях не станет меньше некоторого априори заданного значения.
Формально алгоритм определяется в форме итеративного выполнения следующей последовательности шагов:
1. Предварительно задается количество искомых нечетких кластеров 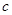 , максимальное число итераций алгоритма
, максимальное число итераций алгоритма 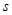 , параметр сходимости алгоритма
, параметр сходимости алгоритма  и экспоненциальный вес нечеткой кластеризации
и экспоненциальный вес нечеткой кластеризации 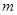 . В качестве текущего нечеткого разбиения на первой итерации алгоритма для матрицы
. В качестве текущего нечеткого разбиения на первой итерации алгоритма для матрицы 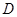 задать некоторое исходное нечеткое разбиение
задать некоторое исходное нечеткое разбиение  на
на 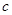 непустых нечетких кластеров, которые описываются совокупностью функций принадлежности
непустых нечетких кластеров, которые описываются совокупностью функций принадлежности  . Если субъективность нечеткого разбиения высока, то предлагается построить матрицу расстояний между объектами по формуле (2.28), определить полярные объекты (наиболее удаленные) и далее перейти к шагу 2, используя в качестве центров кластеров вектора полярных объектов.
. Если субъективность нечеткого разбиения высока, то предлагается построить матрицу расстояний между объектами по формуле (2.28), определить полярные объекты (наиболее удаленные) и далее перейти к шагу 2, используя в качестве центров кластеров вектора полярных объектов.
2. Для исходного текущего нечеткого разбиения 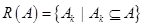 по формуле (2.37) рассчитаем центры нечетких кластеров
по формуле (2.37) рассчитаем центры нечетких кластеров  и значение целевой функции
и значение целевой функции 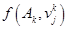 по формуле (2.38). Количество выполненных итераций положить равным 1.
по формуле (2.38). Количество выполненных итераций положить равным 1.
3. Сформировать новое нечеткое разбиение 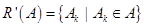 исходного множества объектов кластеризации
исходного множества объектов кластеризации 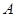 на
на  непустых нечетких кластеров, характеризуемых совокупностью функций принадлежности
непустых нечетких кластеров, характеризуемых совокупностью функций принадлежности 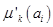 , которые определяются по формуле:
, которые определяются по формуле:
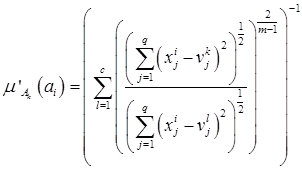 ,
,  .
.
При этом если для некоторого 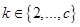 и некоторого
и некоторого 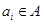 значение
значение 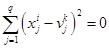 , то для соответствующего нечеткого кластера
, то для соответствующего нечеткого кластера 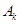 полагаем
полагаем 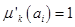 , а для остальных
, а для остальных 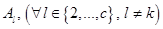 полагаем
полагаем 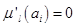 . Если же таких
. Если же таких 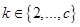 для некоторого
для некоторого 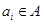 окажется несколько, т.е. для них значение
окажется несколько, т.е. для них значение 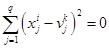 , то эвристически для меньшего из
, то эвристически для меньшего из 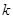 полагаем
полагаем 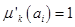 , а для остальных
, а для остальных 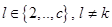 полагаем
полагаем 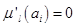 .
.
4. Для нового нечеткого разбиения 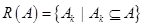 рассчитываем центры нечетких кластеров
рассчитываем центры нечетких кластеров 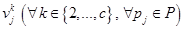 и значение целевой функции
и значение целевой функции 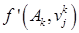 .
.
5. Если количество выполненных итераций превышает заданное число 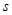 или же модуль разности
или же модуль разности  , т.е. не превышает значения параметра сходимости алгоритма
, т.е. не превышает значения параметра сходимости алгоритма  , то в качестве искомого результата нечеткой кластеризации принять разбиение
, то в качестве искомого результата нечеткой кластеризации принять разбиение  и закончить выполнение алгоритма. В противном случае считать текущим нечетким разбиением
и закончить выполнение алгоритма. В противном случае считать текущим нечетким разбиением  и перейти на третий шаг алгоритма, увеличив на 1 число выполненных итераций.
и перейти на третий шаг алгоритма, увеличив на 1 число выполненных итераций.
Пример 2.11. Применим аппарат нечеткой кластеризации для определения классов студентов, на основании владения теми или иными знаниями и навыками в разработке информационных систем. Приведем характеристику студентов по группе признаков (табл.2.1).
Таблица 2.1.Характеристика студентов по группе признаков
| Студенты | Знание сетевых технологий | Знание современных программных средств | Знание графических пакетов | Навыки построения клиент серверных приложений | Знание аппаратного комплекса | Навыки программирования | Знание Internet технологий | Знание CASE средств | Знание стандартов проектирования | Навыки в администрировании ПО |
| Студент 1 | ||||||||||
| Студент 2 | ||||||||||
| Студент 3 | ||||||||||
| Студент 4 | ||||||||||
| Студент 5 | ||||||||||
| Студент 6 | ||||||||||
| Студент 7 | ||||||||||
| Студент 8 | ||||||||||
| Студент 9 | ||||||||||
| Студент 10 | ||||||||||
| Студент 11 |
Из анализа исключается характеристика «знание современных программных средств» - знание, которым обладают все студенты, поэтому, в данном случае, не являющееся информативным. Разобьем рассматриваемое множество студентов на 3 класса (1 класс: практики в разработке ПО, программисты, разработчики информационных систем), при показателе размытости (нечеткости) равном 1,9 (установленном экспертом), результаты приведем в табл.2.2. С увеличением показателя размытости понижается порог включения в класс равный 0,4.
Таблица 2.2. Веса принадлежности объектов к классам
| Объекты | Классы | |||
| Студент 1 | 0.58 | 0.26 | 0.17 | |
| Студент 2 | 0.77 | 0.15 | 0.09 | |
| Продолжение табл.2.2 | ||||
| Студент 3 | 0.56 | 0.31 | 0.13 | |
| Студент 4 | 0.28 | 0.47 | 0.25 | |
| Студент 5 | 0.28 | 0.48 | 0.24 | |
| Студент 6 | 0.51 | 0.32 | 0.18 | |
| Студент 7 | 0.36 | 0.46 | 0.18 | |
| Студент 8 | 0.19 | 0.27 | 0.54 | |
| Студент 9 | 0.26 | 0.24 | 0.51 | |
| Студент 10 | 0.26 | 0.24 | 0.51 | |
| Студент 11 | 0.20 | 0.21 | 0.58 |
Проводя итерационный процесс уточнения нечеткого разбиения объектов по классам по алгоритму, предложенному ранее (шаг 2- шаг 5), строится табл.2.3. Рассматриваемый алгоритм позволяет также определить, какой набор признаков характерен для каждого класса (табл.2.3).
Таблица 2.3.Центры классов (средневзвешенные значения)
| Классы | Знание сетевых технологий | Знание графических пакетов | Навыки построения клиент серверных приложений | Знание аппаратного комплекса | Навыки программирования | Знание Internet технологий | Знание CASE средств | Знание стандартов проектирования | Навыки в администрировании ПО | |
| студент 1, студент 2, студент 3, студент 6 | 0.958 | 0.827 | 0.829 | 0.733 | 0.198 | 0.745 | 0.079 | 0.079 | 0.023 | |
| студент 4, студент 5, студент 7 | 0.810 | 0.387 | 0.722 | 0.553 | 0.578 | 0.704 | 0.152 | 0.152 | 0.040 | |
| студент 8, студент 9, студент 10, студент 11, | 0.956 | 0.677 | 0.931 | 0.916 | 0.907 | 0.747 | 0.631 | 0.631 | 0.241 |
Результаты проведенного анализа необходимы при построении команд студентов для разработки информационной системы с разделением обязанностей. На основании результатов нечеткой кластеризации студентов по классам, представляется возможность корректировки состава команд на различных этапах проектирования информационных систем.
Дата добавления: 2021-10-28; просмотров: 525;











