Четкость и нечеткость
Ввиду сложности рассматриваемых объектов, существенной нелинейности, трудностей формализации, наличия различных субъективных критериев и ограничений рассмотрим один из видов неопределенности - нечеткость.
Обычно на практике всегда имеется возможность наряду с точечной оценкой параметра (наиболее допустимым его значением) указать минимальное и максимальное значение (интервал), которое может принимать нечеткая величина. Кроме того, можно построить и функцию, характеризующую допустимость каждого значения внутри заданного интервала на основе статистического материала или опроса группы экспертов. Теория нечетких множеств дает возможность проводить вычисления не с одним точечным значением, а с характеристической функцией и получать в результате вычислений нечеткую величину.
Нечеткость может возникать при измерении вполне определенной величины. Поэтому только представление ряда величин как нечетких дает возможность получать устойчивое решение в условиях неопределенности, т.е. в виде функций принадлежности.
В качестве примера рассмотрим такое нечеткое понятие нашей речи, как число «примерно четыре» - это, на самом деле, не число, а множество чисел из интервала [x1; x2]. Каждое из этих чисел, само по себе, является четким объектом, и только при объединении их в нечеткое множество они в какой-то мере обретают нечеткие свойства. Такое объединение происходит всякий раз, как на вопрос: «Который час?» - Нам отвечают: «Примерно четыре...». При этом подразумевается, что это время всегда можно уточнить вплоть до секунды (а в экспериментальной физике его можно уточнить и с гораздо более высокой точностью), попадая в некоторый интервал. Возникает вопрос, существуют ли числа «точно четыре», «точно два с половиной», «точно пи» и можно ли их измерить с подобной точностью? Ведь если такие числа и возникают в наших вычислениях, то только потому, что в качестве исходных мы берем такие же абсолютно точные абстрактные числа. Но если бы в качестве исходных мы брали реальные «примерные» числа, то получали бы такие же «примерные» числа.
В теории нечетких множеств абстрактные числа представляют трапециевидной и треугольной функциями принадлежностей, опирающихся на интервал [х1; х2], другими словами существуют трапециевидные и треугольные нечеткие числа.
Нечеткое число – это нечеткое подмножество универсального множества действительных чисел, имеющее нормальную и выпуклую функцию принадлежности, то есть такую, что:
а) существует такое значение носителя, в котором функция принадлежности равна единице, а также
б) при отступлении от своего максимума влево или вправо функция принадлежности убывает.
Рассмотрим два вида нечетких чисел:
1. Треугольные нечеткие числа
Эти числа моделируют высказывание следующего вида: «параметр А приблизительно равен а и однозначно находится в диапазоне [amin, amax]».

Рис.2.14. Функция принадлежности треугольного нечеткого числа
Треугольные числа – это самый часто используемый на практике тип нечетких чисел, причем чаще всего — в качестве прогнозных значений параметра.
2. Трапециевидное нечеткое число.
Функция принадлежности нечеткого числа m (х) определяемого нечетким понятием «принадлежать диапазону примерно от a до b» имеет трапезоидный вид, как показано на рис.2.15.

Рис.2.15. Функция принадлежности трапециевидного числа
Поскольку границы интервала заданы нечетко, то разумно ввести абсциссы вершин трапеции следующим образом: a = (a1+a2)/2, b = (b1+b2)/2, при этом расстояние между вершинами a 1,a 2иb1, b2 соответственно друг от друга обуславливается тем, какую семантику мы вкладываем в понятие «примерно»: чем больше разброс, тем боковые ребра трапеции являются более пологими.
Если мы оцениваем параметр качественно, например, высказавшись: «Это значение параметра является средним», - необходимо ввести уточняющее высказывание типа: «Среднее значение – это примерно от a до b», - которое есть предмет экспертной оценки (нечеткой классификации), и тогда можно использовать для моделирования нечетких классификаций трапезоидные числа.
Определим соответствующие интервалы достоверности по двум нечетким числам A и B: [a1, a2] и [b1, b2] соответственно. Тогда основные операции с нечеткими числами сводятся к операциям с их интервалами достоверности, а операции с интервалами, в свою очередь, выражаются через операции с действительными числами - границами интервалов:
операция «сложения»: [a1, a2] (+) [b1, b2] = [a1 + b1, a2 + b2],
операция «вычитания»: [a1, a2] (-) [b1, b2] = [a1 - b2, a2 - b1],
операция «умножения»: [a1, a2] (*) [b1, b2] = [a1 * b1, a2 * b2],
операция «деления»: [a1, a2] (/) [b1, b2] = [a1 / b2, a2 / b1],
операция «возведения в степень»: [a1, a2] (^) i = [a1i , a2i].
Нечеткая последовательность - это набор нечетких чисел со своими функциями принадлежности, где каждому нечеткому числу взаимно однозначно соответствует порядковый номер, принадлежащий множеству целых положительных чисел. Если заместить в этом определении набор действительных чисел на несчетное множество точек оси действительных чисел (область определения), а набор нечетких чисел - на несчетное множество нечетких чисел (область значений), то легко перейти к определению нечеткой функциикак взаимно-однозначному соответствию оси действительных чисел и несчетного множества нечетких чисел.
Другой существенной проблемой является процедура преобразования нечеткого множества в четкое число. В теории нечетких множеств эта процедура аналогична нахождения характеристик положения (математического ожидания, моды, медианы) случайных величин в теории вероятности. Простейшим способом выполнения процедуры является выбор четкого числа, соответствующего максимуму функции принадлежности. Однако пригодность этого способа ограничивается лишь одноэкстремальными функциями принадлежности. Для многоэкстремальных функций принадлежности существуют такие методы:
1) Метод центра тяжести или центроидный метод.
Определение центра тяжести функции принадлежности производиться по следующим формулам:
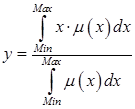
| - для непрерывной функции принадлежности, | (2.39) |
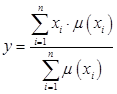
| - для дискретных нечетких множеств, | (2.40) |
где 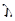 - результат преобразования нечеткого множества в четкое число,
- результат преобразования нечеткого множества в четкое число,
Min, Max- соответственно левая и правая точки интервала носителя нечеткого множества рассматриваемой выходной переменной Х,
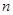 - число элементов, описывающих нечеткое число.
- число элементов, описывающих нечеткое число.
2)Метод медианы.
Определение медианы функции принадлежности для непрерывного универсального заключается в нахождении такого числа а, что:
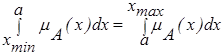
| (2.41) |
В случае дискретного универсального множества определение четкого числа нечеткого множества осуществляется по формуле (2.42).
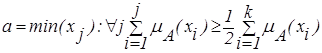
| (2.42) |
3) Метод центра максимумов.
Определение центра максимумов производиться по следующей формуле:
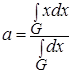 , ,
| (2.43 |
где G – множество всех элементов из интервала [xmin, xmax], имеющих максимальную степень принадлежности нечеткому множеству А.
В методе центра максимумов находится среднее арифметическое элементов универсального множества, имеющих максимальные степени принадлежностей. Если множество таких элементов конечно, то формула упрощается к следующему виду:
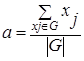 ,
,
где 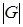 - мощность множества G.
- мощность множества G.
В дискретном случае процесс получения четкого числа по методам наибольшего из максимумов и наименьшего из максимумов осуществляется по формулам 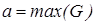 и
и 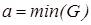 , соответственно. Из приведенных формул видно, что если функция принадлежности имеет только один максимум, то его координата и является четким аналогом нечеткого множества (треугольные нечеткие числа), в противном случае применяются методы, рассмотренные выше (трапециевидные числа).
, соответственно. Из приведенных формул видно, что если функция принадлежности имеет только один максимум, то его координата и является четким аналогом нечеткого множества (треугольные нечеткие числа), в противном случае применяются методы, рассмотренные выше (трапециевидные числа).
Пример 2.12. Определить температуру, наиболее соответствующую нечеткому понятию «теплая погода», заданную нечетким множеством
А= {(0/0),(5/0),(10/0,1),(15/0,5),(20/0,9),(25/1,0),(30/1,0),(35/0,7),(40/0,5)}.
Для преобразования нечеткого множества в четкое число используем метод центра тяжести.
Применяя формулу (2.40), получаем:
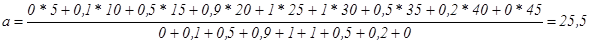
Дата добавления: 2021-10-28; просмотров: 515;











