Уравнения Максвелла

1. Гипотеза Максвелла о вихревом электрическом поле. Анализируя явление электромагнитной индукции, Джеймс Максвелл сделал в 60-х годах XIX в. предположение, что причина появления ЭДС индукции состоит в возникновении электрического поля. Это электрическое поле создаётся изменяющимся магнитным полем. При этом проводники играют второстепенную роль. Они являются своеобразными приборами, обнаруживающими это поле. Под действием поля заряды проводимости в проводнике приходят в движение, и если проводник замкнут, в нём возникает индукционный ток.

Электрическое поле, возникающее при электромагнитной индукции, является вихревым. Его силовые линии замкнуты. ЭДС индукции есть 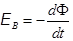, (19.1)

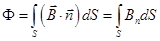где Ф – поток магнитной индукции B через площадку S, ограниченную рассматриваемым контуром (рис.126). В общем случае . (19.2)

Здесь B_n - проекция вектора магнитной индукции B на нормаль n к контуру. С другой стороны, действующая в любом контуре ЭДС может быть представлена как циркуляция вектора электрической напряжённости сторонних сил (см. ф. 8.11).

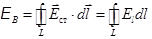. (19.3)

Здесь Е_ст - напряжённость вихревого электрического поля, Е_l – проекция вектора Е_ст на касательную к контуру.

Приравняв правые части выражений (19.2) и (19.3), получаем количественную связь между напряжённостью вихревого электрического поля и скоростью изменения потока.

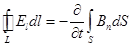. (19.4)

Это уравнение обобщает закон электромагнитной индукции Фарадея. В системе уравнений Максвелла в интегральной форме его обычно записывают вторым.

2. Токи смещения. Гипотеза Максвелла о возникновении вихревого электрического поля, из соображений симметрии, приводит к обратному заключению: всякое изменение электрического поля должно вызывать появление вихревого магнитного поля.

Рассмотрим схему, показанную на рис.127. Если включить конденсатор С в цепь, то пока он заряжается, в цепи через лампочку Л будет проходить электрический ток. При изменении переключателем Пк полярности включения конденсатора ток через конденсатор потечёт в обратном направлении до полной перезарядки. Если после каждой перезарядки переключателем Пк менять полярность включения конденсатора, можно заставить лампочку светиться практически непрерывно. Через лампочку течёт пульсирующий ток одного направления, а через конденсатор – ток переменного направления.

Итак, в отличие от постоянных переменные токи могут существовать и в разомкнутых цепях (в конденсаторе разрыв цепи). В проводниках при этом движутся заряды проводимости, а в пространстве между пластинами конденсатора существует лишь переменное электрическое поле. Поскольку в этом поле происходит переменная поляризация диэлектрика, то есть переменное смещение связанных зарядов диэлектрика, Максвелл назвал его током смещения. Можно сказать, что ток проводимости в проводнике замыкается током смещения в диэлектрике.

3. Первое уравнение Максвелла в интегральной форме.

Согласно Максвеллу, переменное электрическое поле в конденсаторе в любой момент времени создаёт такое же магнитное поле, как если бы между обкладками существовал ток проводимости, равный току в проводниках. Иначе, магнитное поле разомкнутого контура такое же, как если бы контур был замкнут. Это предположение позволяет установить количественную связь между изменяющимся электрическим полем и генерируемым им магнитными полем.

Ток в проводнике можно определить как скорость изменения заряда на обкладках конденсатора 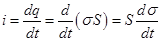, (19.5)

где σ – поверхностная плотность зарядов на обкладках площадью S. Разделив на S, получаем плотность тока 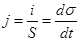. (19.6)

Если плотность зарядов σ выразить через напряжённость электрического поля в конденсаторе из формулы (7.8), σ = εε₀Е, и сохранить векторный характер величин j и Е, то получаем плотность тока смещения 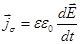. (19.7)

Переменное во времени электрическое поле создаёт такое же магнитное поле, как и ток проводимости плотностью .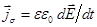

В любой точке проводника может существовать как ток проводимости, так и ток смещения. Поэтому плотность полного тока j_S равна их сумме. 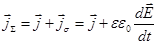. (19.8)

Если в проводнике выделить малую площадку S, ограниченную контуром L (рис.128), то по закону полного тока (формула 13.6) можно записать: 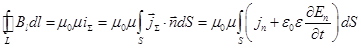. (19.9)

Здесь i_S - полный ток, j_n - проекция вектора плотности тока проводимости на нормаль к площадке, Е_n – проекция вектора напряжённости электрического поля на нормаль к площадке. Поскольку интегрирование выполняется по площади, то есть по координатам, то в подинтегральной функции производная по времени является частной и обозначается ∂.

Интеграл от напряжённости можно преобразовать. С учётом электростатической теоремы Гаусса (формула 4.4) получаем 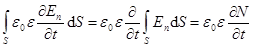. (19.10)

Здесь N – поток вектора электрической напряжённости через площадку S. Интеграл от плотности тока проводимости даёт ток проводимости i через площадку S: 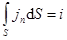. (19.11)

После подстановки получаем первое уравнение Максвелла 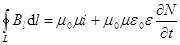. (19.12)

Это уравнение обобщает законы Ампера и Био-Савара-Лапласа.

4. Опыты Роуланда и Эйхенвальда. То, что магнитное поле возникает вокруг проводника с током ещё не означает, что поле создаётся движущимися электрическими зарядами. Не исключалось, что магнитное поле создаёт проводник, переходящий в некое новое качество, когда в нём существует электрический ток. Поэтому было важно на опыте доказать, что магнитное поле создаётся любыми электрическими зарядами, движущимися в любой среде. Тем самым магнитное поле токов смещения из гипотезы превращалась бы в реальный факт.

В 1878 г. в лаборатории Гельмгольца американец Генри Роуланд с целью проверки гипотезы Максвелла поставил следующий опыт. Эбонитовый диск толщиной 0,5 см и диаметром 21 см имел на верхней поверхности кольцеобразный носитель электричества – разрезанное в точках а и в кольцо из золочёной фольги (рис.129, вверху). Диск устанавливался на оси и помещался в заземлённую металлическую коробку (рис.129, внизу). Коробка и кольцевой носитель представляли собой конденсатор, ёмкость которого было нетрудно вычислить или измерить. Если к носителю приложить относительно коробки напряжение U, то, зная ёмкость системы, можно всегда определить заряд q на носителе (Чтобы предотвратить случайное стекание заряда при отключении от источника, заряд q обычно подавался на носитель с острия с расстояния 0,3 мм). Значение q составляло около 10^-7 Кл.

Над коробкой помещался магнетоскоп М – подвешенная на тонкой нити маленькая магнитная стрелка с зеркальцем, ориентированная в состоянии покоя касательно диску.

Когда диск вращался с частотой около ν = 60 об/с, движущийся с кольцевым носителем заряд создавал круговой ток. В результате магнитная стрелка отклонялась, что говорило о появлении магнитного поля.

Количественная проверка состояла в следующем. Диск останавливался, к точкам а и в носителя подключались проводники, и через кольцевой носитель пропускался такой ток проводимости, при котором магнитная стрелка отклонялась на ту же величину.

Сравнение конвективного тока i = q ν, обусловленного вращением носителя, с током проводимости показало, что токи совпадают.

Опыты Роуланда повторялись с разными результатами и другими исследователями, пока в 1901 – 1904 г.г. русский физик Александр Эйхенвальд окончательно не доказал, что все наблюдаемые в экспериментах токи – проводимости, конвективные и токи смещения – всегда образуют собой замкнутые цепи и генерируют магнитные поля.

5. Система уравнений Максвелла в интегральной форме. Всё содержание теории электромагнетизма может быть сконцентрировано в группе математических соотношений, полученных Максвеллом в 60-х годах XIX в. на основе обобщения эмпирических законов электрических и магнитных явлений.

1-е уравнение.	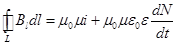.	Закон полного тока (Закон Ампера).	(19.13)
2-е уравнение.	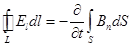.	Закон электромагнитной индукции	(19.14)
3-е уравнение.	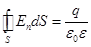.	Закон Кулона в форме теоремы Гаусса (см. ф. 6.9).	(19.15)
4-е уравнение.	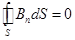.	Закон отсутствия в природе магнитных зарядов.	(19.16)

Эти 4 уравнения называются уравнениями поля.

Полная система уравнений, описывающих поля и заряды, включает в себя кроме уравнений поля выражения для сил, действующих на заряды (14.12), и законы динамики Ньютона, описывающие движение носителей зарядов под действием этих сил.

Взаимодействие полей с материальными средами описывается с помощью макроскопических параметров ε, μ, g, значения которых могут быть в первом приближении вычислены в рамках моделей микроскопической электродинамики. Электромагнитные явления в области атомных размеров и внутри самих атомов и молекул могут быть описаны только с помощью квантовой электродинамики.

6. Значение системы уравнений Максвелла.

Уравнения Максвелла описывают огромную область явлений. Они лежат в основе электротехники и радиотехники, играют важнейшую роль в таких разделах физики как управляемый термоядерный синтез, физика плазмы, магнитогидродинамика, нелинейная оптика, астрофизика и др. Уравнения Максвелла неприменимы лишь при больших частотах электромагнитных колебаний, когда становятся заметными квантовые эффекты.

В конце XIX – начале XX в.в. Хендрик Лоренц построил классическую электронную теорию вещества, иначе, микроскопическую электродинамику. В этой теории вещество рассматривается как совокупность электрически заряженных частиц – электронов и атомных ядер, движущихся в вакууме. См., напр., теорию проводимости Друде-Лоренца, с.___. Преобразовав макроскопические уравнения Максвелла к микроскопическим полям, Лоренц получил систему уравнений, описывающих поля в любой момент времени и в любой точке пространства, в том числе между атомами и внутри атомов. Эти уравнения называют уравнениями Максвелла-Лоренца.

Электронная теория Лоренца позволяет выяснить физический смысл материальных констант, входящих в уравнения Максвелла - ε, μ, g. В вакууме уравнения Лоренца совпадают с уравнениями Максвелла.

На очень малых пространственно-временных интервалах законы классической электронной теории не выполняются. Она уступает место квантовой теории электромагнитных процессов – квантовой электродинамике. Если в классической электронной теории электромагнитное поле считается непрерывным, то в квантовой электродинамике оно дискретно и состоит из квантов энергии – фотонов.