Пара - и ферромагнетики
1. Парамагнетики – это вещества, у которых μ > 1 и χ > 0. К ним относятся щелочные металлы, Ca, Mg, Cr, Mn, Sn, Pb, редкоземельные элементы и другие.
В отсутствие внешнего магнитного поля магнитный момент каждого отдельного атома парамагнетика не равен нулю, как в диамагнетиках. Но моменты атомов ориентированы хаотично, поэтому магнитный момент единицы объём (вектор намагничения) парамагнетика в отсутствие внешнего поля также равен нулю.
При включении внешнего поля моменты атомов начинают прецессировать вокруг оси, параллельной линиям поля. В результате появляется отличная от нуля проекция магнитных моментов атомов на эту ось. Поле в магнетике усиливается. (См. §14, пункт 1).
| Таблица 18.1 | ||
| Вещество | μ | χ, 10-6 |
| Алюминий Al | 1, 000 023 | +23 |
| Ванадий V | 1, 000 343 | +343 |
| Вольфрам W | 1, 000 176 | +176 |
| Магний Mg | 1, 000 017 | +17 |
| Марганец Mn | 1, 001 000 | +1000 |
| Олово Sn | 1, 000 002 | +2 |
| Платина Pt | 1, 000 250 | +250 |
| Хром Cr | 1, 000 330 | +330 |
Из-за теплового движения ориентация атомных магнитных моментов является частичной, поэтому при несильных магнитных полях намагниченность парамагнетика растёт линейно с индукцией поля В. 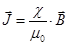 . (18.1)
. (18.1)
В парамагнетиках также существует диамагнетизм, но здесь он лишь уменьшает магнитные моменты атомов и перекрывается эффектом ориентации магнитных моментов атомов по внешнему полю. Поэтому суммарная магнитная восприимчивость парамагнетиков положительна, χ > 0 (таблица 18.1).
Термин “диа-” и “парамагнетизм” ввёл в 1945 г. М. Фарадей.
2. Закон Кюри для парамагнетиков. С повышением температуры Т при неизменной индукции внешнего поля возрастает дезориентирующее действие теплового движения частиц. Поэтому магнитная восприимчивость парамагнетиков в простейшем случае убывает по закону Кюри. 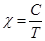 , (Пьер Кюри, 1895) (18.2)
, (Пьер Кюри, 1895) (18.2)
где С – постоянная Кюри, зависящая от природы вещества.
Закону Кюри подчиняются газы (О2 , NO), пары щелочных металлов, разбавленные жидкие растворы парамагнитных солей редкоземельных элементов.
Кристаллические парамагнетики лучше следуют закону Кюри – Вейсса
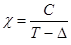 , (Пьер Вейсс, 1907) (18.3)
, (Пьер Вейсс, 1907) (18.3)
где С и Δ – константы вещества.
3. Природа парамагнетизма. Существование у атомов магнитных моментов, обуславливающих парамагнетизм веществ, связано с движением электронов в оболочке атома (орбитальный парамагнетизм), со спиновым моментом электронов (спиновый парамагнетизм), с магнитными моментами ядер атомов (ядерный парамагнетизм). Магнитные моменты атомов и молекул создаются, в основном, спиновыми и орбитальными моментами их электронных оболочек. Они примерно в 1000 раз превосходят магнитные моменты атомных ядер.
Парамагнетизм металлов слагается из парамагнетизма электронов проводимости и парамагнетизма электронных оболочек атомов кристаллической решётки. Движение электронов проводимости в металлах практически не меняется при изменении температуры (см. §9). Поэтому и парамагнетизм, обусловленный электронами проводимости, также не зависит от температуры.
Например, электронные оболочки ионов щелочных и щелочноземельных металлов не имеют магнитных моментов. Парамагнетизм этих элементов обусловлен исключительно электронами проводимости. Поэтому их магнитная восприимчивость практически не зависит от температуры.
В 1906 г Поль Ланжевен построил классическую теорию парамагнетизма. Для вещества парамагнетика, состоящего из практически невзаимодействующих атомов, магнитная восприимчивость в его теории определена формулой 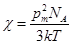 , (18.4)
, (18.4)
где k – постоянная Больцмана, pm – магнитный момент атома, NA – число Авогадро, Т – температура.
4. Ферромагнетики (от лат. ferrum – железо) – твёрдые кристаллические вещества, обладающие по сравнению с парамагнетиками высокой способностью намагничения. Магнитная проницаемость μ ферромагнетиков может достигать десятков и сотен тысяч.
Явление ферромагнетизма было открыто в начале XIX века после появления источников тока Вольты. Оказалось, что железный сердечник, внесённый в соленоид, при том же намагничивающем токе сильно увеличивает способность соленоида притягивать к себе железные опилки.
Ферромагнетизм существует только у веществ с парамагнитными атомами, магнитные моменты которых не равны нулю. В объёме ферромагнетика самопроизвольно образуются микроскопические области – домены, в пределах которых магнитные моменты атомов сонаправлены. Это квантовый эффект. При температурах ниже некоторого предела (точки Кюри) эти домены существуют независимо от наличия внешнего магнитного поля. Феноменологически домены удобно трактовать по Амперу как воображаемые микроконтуры с круговым током. Поскольку магнитные моменты доменов ориентированы хаотично, то усреднённое по макрообъёму поле в ненамагниченных ферромагнетиках равно нулю. При внесении ферромагнетика во внешнее поле моменты доменов стремятся повернуться по полю (см. §14 пункт 2). В результате магнитное поле внутри ферромагнетика усиливается.
Размеры доменов на три порядка больше размера атомов. Поэтому тепловое движение нарушает ориентацию доменов по полю слабее, чем ориентацию отдельных атомов парамагнетика. Однако при достижении определённой для каждого материала температуры намагниченность доменов скачком исчезает, и ферромагнетик превращается в парамагнетик. Эта предельно высокая температура называется точкой Кюри. В точке Кюри происходит фазовый переход 2-го рода. При этом одновременно скачкообразно изменяются удельная электропроводность и теплоёмкость вещества.
Среди химических элементов ферромагнетиков не много. Наиболее заметно ферромагнетизм выражен у железа, кобальта, никеля. Максимальное значение магнитной проницаемости μmax составляет у них сотни и тысячи единиц (таблица 18.2). Внешние электроны у этих металлов находятся в 3d состоянии.
| Элемент | μмакс | Точка Кюри | |
| К | ˚С | ||
| Железо Fe литое | 24 000 | ||
| -²- электролитическое | 340 000 | ||
| -²- монокристалл | 1 430 000 | ||
| Кобальт Co | |||
| Никель Ni | 1 120 | ||
| Гадолиний Gd | |||
| Тербий Tb | -50 | ||
| Диспрозий Dy | -186 | ||
| Гольмий Ho | -253 | ||
| Эрбий Er | 19,6 | -253,4 |
Таблица 18.2Ферромагнетизм редкоземельных металлов гадолиния Gd, тербия Tb, диспрозия Dy, гольмия Ho и эрбия Er выражен слабее. Наблюдать и использовать его трудно из-за низких значений точки Кюри.
 5. Изменение магнитной индукцииВ поля в ферромагнетиках можно сделать как на основе закона электромагнитной индукции Фарадея с помощью тороидального сердечника из исследуемого материала. В сердечнике пропиливается узкий разрез так, чтобы его ширина l была по крайней мере на два порядка меньше осевой длины сердечника, l << 2pR (рис.123). Это условие позволяет пренебречь рассеиванием магнитного поля в разрезе и полагать, что индукция В в зазоре такая же, как и внутри сердечника. Если по первичной обмотке с числом витков n1 пропускать намагничивающий ток i1 , то в сердечнике и в зазоре будет возбуждаться магнитное поле В с потоком Ф = BS , где S – площадь сечения сердечника.
5. Изменение магнитной индукцииВ поля в ферромагнетиках можно сделать как на основе закона электромагнитной индукции Фарадея с помощью тороидального сердечника из исследуемого материала. В сердечнике пропиливается узкий разрез так, чтобы его ширина l была по крайней мере на два порядка меньше осевой длины сердечника, l << 2pR (рис.123). Это условие позволяет пренебречь рассеиванием магнитного поля в разрезе и полагать, что индукция В в зазоре такая же, как и внутри сердечника. Если по первичной обмотке с числом витков n1 пропускать намагничивающий ток i1 , то в сердечнике и в зазоре будет возбуждаться магнитное поле В с потоком Ф = BS , где S – площадь сечения сердечника.
Внесём в зазор плоскую измерительную катушку с числом витков n2 , концы которой присоединены к баллистическому гальванометру БГ. (Его описание см. в работе 15 лабораторного практикума по физике, часть 3, электричество, с.77). Дождавшись успокоения стрелки гальванометра, быстро выдёргиваем катушку.
Поскольку магнитный поток, пронизывающий катушку, меняется при этом от Ф2 до 0, по цепи измерительной катушки проходит заряд q = kФ2 . Если площадь сечения катушки S2 < S, то Ф2 = ФS2çS. Коэффициент пропорциональности k определяется параметрами установки. Найдём его. ЭДС индукции в измерительной катушке
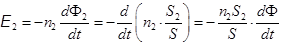 . (18.5)
. (18.5)
Если сопротивление цепи измерительной катушки равно r2 , то по ней протекает индукционный ток 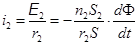 , или
, или 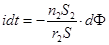 . (18.6)
. (18.6)
После интегрирования получаем: 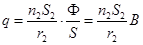 , Þ
, Þ 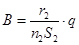 . (18.7)
. (18.7)
Магнитную проницаемость m вещества тороида можно найти из формулы (13.9), определяющей индукцию поля В в тороиде, где R – радиус осевой окружности тороида.
 , Þ
, Þ 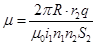 . (18.8)
. (18.8)
Рассмотренный здесь метод измерения В и m приближённый, поскольку мы пренебрегаем магнитным сопротивлением разреза в тороиде. Но он прост в реализации и в теории. Более точные методы, не требующие разрезания сердечника, основаны на переменных токах.
6. Магнитный гистерезис. Первым подробно изучал намагничивание мягкого железа в 1878 г. Александр Столетов. Результаты, к которым он пришёл, в следующем.
Перед началом измерений исследуемый ферромагнетик нужно прокаливать (нагревать выше точки Кюри), благодаря чему исчезает его остаточная намагниченность. Установка примерно соответствовала схеме на рис.123.
Вначале постепенно увеличивался, а затем уменьшался до нуля намагничивающий ток i1 . При каждом токе баллистическим гальванометром измерялась индукция В. После этого переключателем Пк направление тока i1 менялось, и измерения индукции В повторялись уже при токе i1 другого направления.
 Зависимость B(i1), показанная на рис.124, называется петлёй гистерезиса (от греч. hysteresis - отставание). Чтобы графики, полученные для разных образцов с разной геометрией, можно было сравнивать между собой, по горизонтальной оси откладывают не тока i1 , а пропорциональный току параметр H = n1 i1 / 2 p R. Это следует из формулы (13.9) для магнитной индукции поля в тороиде,
Зависимость B(i1), показанная на рис.124, называется петлёй гистерезиса (от греч. hysteresis - отставание). Чтобы графики, полученные для разных образцов с разной геометрией, можно было сравнивать между собой, по горизонтальной оси откладывают не тока i1 , а пропорциональный току параметр H = n1 i1 / 2 p R. Это следует из формулы (13.9) для магнитной индукции поля в тороиде, 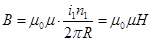 . (18.9)
. (18.9)
Если бы магнитная проницаемость m вещества тороида оставалась постоянной, то начальная кривая намагничивания ОА была бы прямой линией.
Найденная Столетовым зависимость m(Н) показана на рис.125. Вначале m быстро растёт до mmax , затем начинает уменьшаться и при больших намагничивающих токах стремится к 1. Ферромагнетик переходит в состояние насыщения, на петле гистерезиса оно начинается с точки А. Далее рост индукции В идёт исключительно за счёт увеличения тока намагничивания i1.
Благодаря насыщению намагничивания использование ферромагнитных сердечников для получения сильных полей, больших 1 Тл, бесполезно. Сильные и сверхсильные магнитные поля получают с помощью катушек с током без ферромагнитных сердечников.
 При уменьшении тока i1 индукция В убывает по кривой АС. При i1 = 0 B ¹ 0. Железный сердечник сохраняет остаточную намагниченность Вост , которая позволяет делать из железа постоянные магниты. Чтобы устранить намагниченность сердечника, нужно пропускать ток i1 обратного направления и такой величины, чтобы параметр Н соответствовал точке D.
При уменьшении тока i1 индукция В убывает по кривой АС. При i1 = 0 B ¹ 0. Железный сердечник сохраняет остаточную намагниченность Вост , которая позволяет делать из железа постоянные магниты. Чтобы устранить намагниченность сердечника, нужно пропускать ток i1 обратного направления и такой величины, чтобы параметр Н соответствовал точке D.
При дальнейшем нарастании обратного тока i1 в точке Е также достигается состояние насыщения, и далее процесс идёт аналогично. Значения параметра H, соответствующего точкам D и G, при котором снимается остаточная намагниченность, называется коэрцитивной силой (от лат. coercitio - удерживаю).
Если образец доходит до состояния насыщения (точки А и Е), то получается максимальная петля гистерезиса. Если насыщение не достигается, Петля называется частной. Она всегда находится внутри максимальной петли.
Суть явления гистерезиса в том, что на величину магнитной индукции В влияет предыстория состояния ферромагнетика. Благодаря этому одному и тому же значению намагничивающего тока i1 в области начальной кривой соответствуют 3 разных значения В (точки пересечения с вертикалью при i = I на рис.124).
Чтобы перемагнитить образец, ток i1 должен совершать работу, которая пропорциональна площади петли гистерезиса. Эта работа превращается в тепло. Материалы с малой площадью петли называются магнитно–мягкими. Они сравнительно мало нагреваются и применяются в цепях переменных токов. Материалы с большой площадью петли называются магнитно–жёсткими. Из них делают постоянные магниты.
7. Магнитострикция (от магнито – и лат. strictio – сжатие, натягивание) – изменение формы и размеров магнетика при намагничивании. Наиболее заметна и имеет практическое значение магнитострикция в ферромагнетиках. В диа- и парамагнетиках она ничтожна. Открыл магнитострикцию Джеймс Джоуль в 1842 г.
Это явление обусловлено тем, что в результате намагничивания образца поворачиваются магнитные моменты доменов и смещаются их границы. Это приводит к изменению энергетического состояния кристаллической решётки и к изменению её межузельных расстояний. Мерой магнитострикции является коэффициент 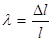 , (18.10)
, (18.10)
где Dl – абсолютное удлинение образца, l – его длина.
Если образец сжимается, то Dl и l - отрицательные числа. У чистых металлов хорошо заметна магнитострикция никеля, для которого l = - 3×10-5. У редкоземельного диспрозия l на три порядка больше. Но из-за низкой точки Кюри (87 К) практически не используется. Значения l для некоторых магнитных материалов приведены в таблице 18.3.
Магнитострикция широко применяется в гидролокации. Если обмотку ферромагнетика питать током резонансной частоты, соответствующей размеру и упругости сердечника, то амплитуда колебаний сердечника может достигать заметной величины. В результате получается магнитострикционный излучатель ультразвуковой частоты в десятки и сотни килогерц. Помещённый в воду, такой излучатель создаёт в ней ультразвуковые волны. Отражённые от подводных и надводных объектов и принятые на корабле, они несут информацию о гидрологической обстановке.
8. Магнитные материалы. Чистые ферромагнитные элементы практически не используются. Применяют обычно сплавы и керамики. Из сплавов наиболее применимы электротехнические стали и сплавы на основе железа с добавками. А из керамик – ферриты–кристаллические твёрдые растворы оксида железа Fe2O3 c одним или несколькими оксидами Li, Zn, Ni, Cd, Pb и других металлов.
Индукция поля в ферритах ниже, чем в сплавах и не превышает 0,4 Тл. Но электрическое сопротивление ферритов очень велико и на 3-10 порядков превышает сопротивление сплавов. Поэтому в ферритах практически нет вихревых индукционных токов. Это позволяет использовать ферриты в высокочастотных цепях в качестве сердечников трансформаторов, в импульсных устройствах и т.д.
Характеристики некоторых магнитных материалов приведены в таблице 18.3. В столбце “Состав” в скобках указано весовое процентное содержание вещества в материале. Далее приняты обозначения: ВS – магнитная индукция в состоянии насыщения, ma и mmax – начальная и максимальная магнитная проницаемость, r - электрическое сопротивление, l - коэффициент магнитострикции.
Таблица 18.3
| Материал | Состав | ВS,Тл | ma | mmax | r, Ом×м | lS ×106 |
| Сталь электр. | Fe + S + C + Mn +P + S + Cu | 2,2 | 4 500 | 10-5 | -20 | |
| Пермаллой | Ni(50) + Fe(50) | 1,6 | 2 000 | 50 000 | 5×10-5 | -20 |
| Супермаллой | Ni(79) + Mo(5) + Fe | 0,8 | 80 000 | 900 000 | 6×10-5 | -25 |
| Пермендюр | Co(49) + V(2) + Fe | 2,5 | 4 500 | 3×10-5 | +65 | |
| Феррит Ni Zn | ZnO(34) + NiO(16) + Fe2O3(50) | 0,3 | 7 000 | 10-5 | ||
| Феррит MgMn | MgO(25) + MnO(25) + Fe2O3(50) | 0,2 | 1 600 | 10-5 | ||
| Феррит Ni Co | NiO(1) + CoO(2) + Fe2O3(97) | 1 000 | 10-5 | -25 | ||
| Сплав Ф.Гейслера | Cu(75) + Mn(14) + Al(10) |
Дата добавления: 2018-05-10; просмотров: 1440;











