Второе уравнение Максвелла

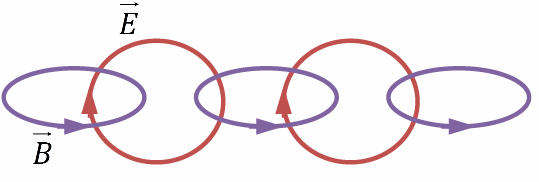
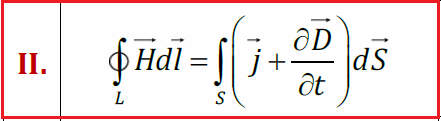Переменное электрическое поле порождает переменное магнитное поле. При этом .

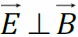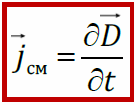Магнитное поле порождается токами: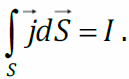

Второе слагаемое в правой части II уравнения Максвелла – плотность тока смещения.

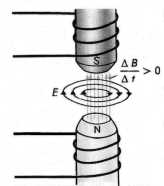
Причина возникновения электрического тока в неподвижном проводнике - электрическое поле.Всякое изменение магнитного поля порождает индукционное электрическое поле независимо от наличия или отсутствия замкнутого контура, при этом если проводник разомкнут, то на его концах возникает разность потенциалов; если проводник замкнут, то в нем наблюдается индукционный ток.

Индукционное электрическое поле является вихревым.
Направление силовых линий вихревого эл. поля совпадает с направлением индукционного тока.

Индукционное электрическое отличается от электростатического поля.

электростатическое поле	индукционное электрическое поле ( вихревое электр. поле )
1. создается неподвижными электр. зарядами	1. вызывается изменениями магнитного поля
2. силовые линии поля разомкнуты - -потенциальное поле	2. силовые линии замкнуты - - вихревое поле
3. источниками поля являются электр. заряды	3. источники поля указать нельзя
4. работа сил поля по перемещению пробного заряда по замкнутому пути = 0.	4. работа сил поля по перемещению пробного заряда по замкнутому пути = ЭДС индукции

Магнитное поле в веществе. Магнитные моменты атомов. Опыт Эйнштейна и де Гааза. Типы магнетиков. Элементарная классическая теория диа- и парамагнетиков. Условия на границе раздела двух сред.

Магнитное поле в веществе является суперпозицией двух полей: внешнего магнитного поля, создаваемого макротоками и внутреннего или собственного, магнитного поля, создаваемого микротоками. Характеризует магнитное поле в веществе вектор , равный геометрической сумме В_внеш и В_внутр магнитных полей.

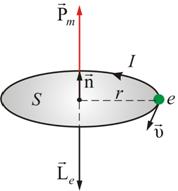
Каждый электрон в атоме (молекуле), двигаясь вокруг ядра, создаёт микроток и собственное магнитное поле; это движение характеризуется микротоком i и магнитным моментом p_m 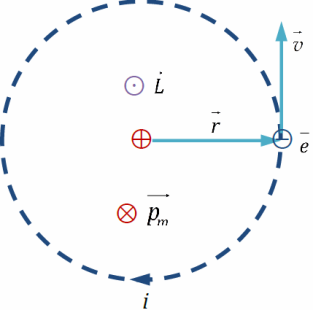Электрон, движущийся по орбите вокруг ядра, представляет собой микроток. Так как заряд электрона отрицательный, сила тока iнаправлена против скорости v, а магнитный момент электронаp_m – против момента импульса L. Модуль магнитного момента электрона

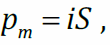
где S = πr2 (r– радиус орбиты) – площадь орбиты;

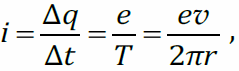
- сила тока, где T – период обращения электрона по орбите;

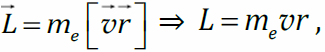- момент импульса, где m_e– масса электрона. Подставим:

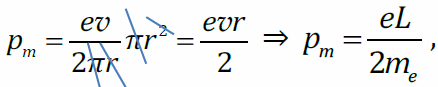
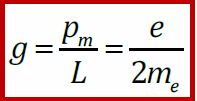- Гиромагнитное отношение орбитальных моментов не зависит от r, v и т. п., а является характерной константой

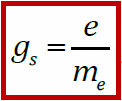Гиромагнитное отношение спиновых моментов

Помимо момента импульса и магнитного момента, описывающих орбитальное движение, электрон обладает ещё и собственным моментом импульса и магнитным моментом – спином

Эффект Эйнштейна и де Гааза — один из магнитомеханических эффектов, состоит в том, что тело (ферромагнетик) при намагничивании вдоль некоторой оси приобретает относительно неё вращательныйимпульс, пропорциональный приобретённой намагниченности.

Ученые наблюдали поворот свободно подвешенного на тончайшей кварцевой нити железного стержня при его намагничении во внешнем магнитном поле (по обмотке соленоида пропускался переменный ток с частотой, равной частоте крутильных колебаний стержня).Было доказано, что кроме орбитальных моментов электрон обладает собственным механическим моментом импульса L_e, называемым спином. Спину электрона L_e, соответствует собственный (сотовый) магнитный момент р_m, пропорциональный L_eи направленный в противоположную сторону. Ученые также доказали,что гиромагнитное отношение орбитальных моментов в 2 раза болше, чем гиромагнитное отношение спиновых моментов (формулы выше).

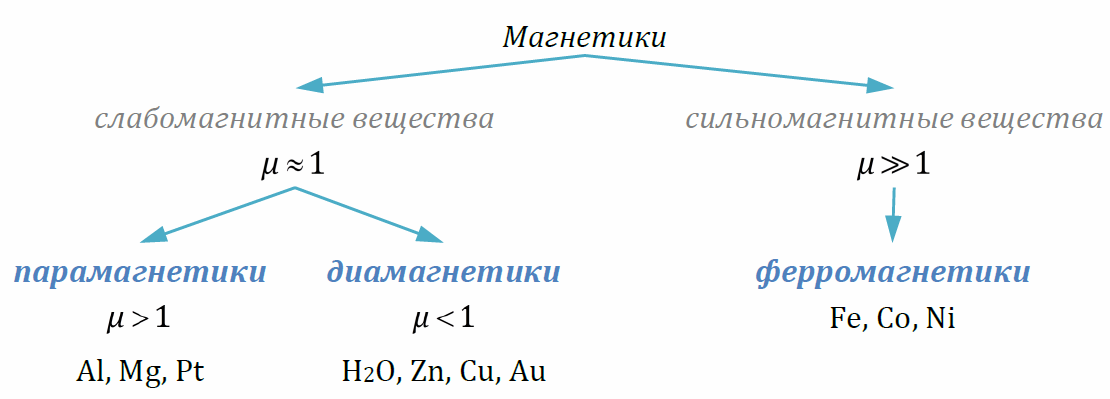Магнетиками называются вещества, которые при внесении во внешнее магнитное поле изменяются так, что сами становятся источниками дополнительного магнитного поля (намагничиваются). При этом полная индукция магнитного поля равна векторной сумме индукций внешнего магнитного поля и магнитного поля порождаемого магнетиком.

Диамагнетизм —свойство тел намагничиваться в направлении, противоположном действующему на них внешнему магнитному полю.Диамагнетикаминазываются вещества, магнитные моменты атомов которых в отсутствии внешнего поля равны нулю, т.к. магнитные моменты всех электронов атома взаимно скомпенсированы (например инертные газы, водород, азот и др.)

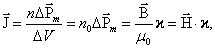Вектор намагниченности диамагнетика равен:

где n₀ – концентрация атомов, μ₀– магнитная постоянная,χ–магнитная восприимчивость среды.

Парамагнетизм- свойство веществ во внешнем магнитном поле намагничиваться в направлении этого поля. При внесении диамагнитного вещества в магнитное поле его атомы приобретают наведенные магнитные моменты.

Парамагнетикаминазываются вещества, атомы которых имеют, в отсутствие внешнего магнитного поля, отличный от нуля магнитный моментp_m_.

Так как диамагнитный эффект обусловлен действием внешнего магнитного поля на электроны атомов вещества, то диамагнетизм свойствен всем веществам. Однако наряду с диамагнитными веществами существуют и парамагнитные— вещества, намагничивающиеся во внешнем магнитном поле по направлению поля.

Условия на границе раздела двух магнетиков

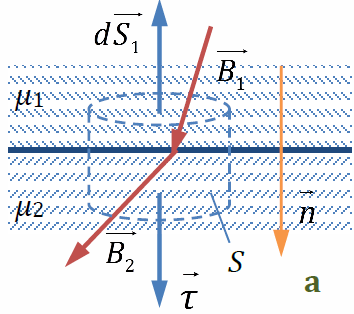
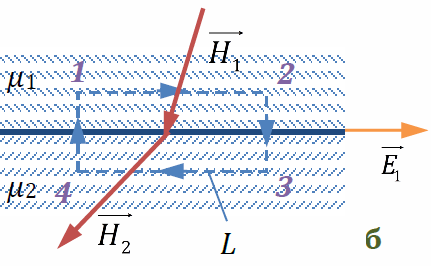Проанализируем, как изменяется магнитное поле при переходе из одной среды (магнетика) в другую. Пусть имеются два изотропных магнетика (относительные магнитные проницаемости μ1 и μ2), граничащие друг с другом. В среде с μ1 существует магнитное поле с индукцией B₁ и напряжённостью H₁. Макротоки на границе раздела сред отсутствуют. Найдём векторные характеристики поля в среде с μ2 – B₂ и H₂. Выберем поверхность интегрирования S в виде цилиндра, основания которого параллельны границе раздела сред, а высота мала . Магнитный поток:

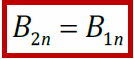– нормальная составляющая вектора магнитной индукции не претерпевает скачка на границераздела магнетиков.

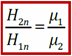Связь B и H в изотропном магнетике 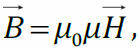поэтому

– нормальная составляющая напряжённости магнитного поля претерпевает скачок на границе раздела магнетиков.

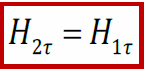– тангенциальная составляющая напряжённости магнитного поля не претерпевает скачка на границе раздела магнетиков.

Из связи 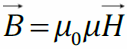и условия 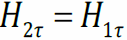получим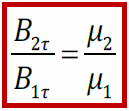

– тангенциальная составляющая магнитной индукции претерпевает скачок на гра-нице раздела магнетиков.

<15 161718 19 20 21 >

Дата добавления: 2016-07-05; просмотров: 3012;