Глава 4. Электромагнитные колебания и волны

Переменный ток

1.Получение гармонического тока промышленной частоты. Переменным называется ток электрических зарядов, величина и направление которого изменяются во времени. Закон изменения тока может быть каким угодно. Но в практике наиболее важны гармонические токи, их величина изменяется во времени по закону синуса или косинуса. Если частота изменений тока не превышает нескольких сотен герц, её называют промышленной. Переменные токи промышленной частоты используются в качестве носителей энергии.

Гармоническую ЭДС промышленной частоты можно получить путём механического вращения замкнутого контура в магнитном поле (рис.130).

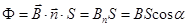Если S – площадь контура, а n - его единичная нормаль, то магнитный поток, пронизывающий контур, есть . (20.1)

Если контур покоится, то Ф = const, и ЭДС индукции в контуре нет.

При вращении жёсткого контура (S = const) в однородном магнитном поле (B= const) в нём наводится ЭДС индукции 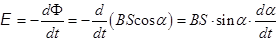. (20.2)

Технически удобнее реализовать равномерное вращение контура, когда a = w×t, где w - угловая скорость вращения. Отсюда daçdt = w и = BSwsinwt = E_asinwt (20.3)

Здесь E_a = BSw - амплитуда ЭДС. (20.4)

Если контур замкнут на некоторое сопротивление R, то под действием переменной ЭДС в контуре возникает переменный ток той же частоты, колебания которого совпадают по фазе с колебаниями ЭДС. 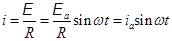(20.5)

Здесь 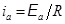- амплитудный ток. Частота колебаний тока n = wç2p, период Т = 1çn = 2pçw.

2. Квазистационарные токи – это такие переменные токи, при которых мгновенные значения тока практически одинаковы во всех точках цепи.

Так как распространение электрического и магнитного полей в пространстве происходит с конечной скоростью, то для того, чтобы в самых отдалённых участках цепи “почувствовалось” изменение ЭДС, должно пройти некоторое время t. Если ЭДС изменяется очень быстро, то напряжённость электрического поля в удалённых точках цепи не успевает за изменением ЭДС.

Если l – линейный размер контура, с – скорость распространения в контуре электромагнитной волны, то t = lçc. Время полного изменения ЭДС равно периоду Т. Если период Т много больше времени t, то ток является квазистационарным.

Т >> lçc, или Tc >> l, или длина цепи l << l - длины электромагнитной волны, соответствующей переменному току. Критическое значение частоты n в цепи n_max = сçl. При l = 1000 км, с = 3×10⁸ м/с, n_max = 3×10⁸ç10⁶ = 300 Гц.

3. Действующее и среднее значение переменного тока. Переменный ток, так же как и постоянный, производит различные действия – тепловые, магнитные, оптические, физиологические. Поэтому для характеристики переменного тока во многих случаях удобнее указывать не группу параметров – амплитуду, фазу и частоту, а величину постоянного тока, производящего такое же действие, как и данный переменный. В качестве такого действия принято брать тепловой эффект. Найдём соотношение между эффективным (действующим) и амплитудным токами.

За один период Т переменный ток выделяет тепло 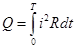. (20.6)

Но такое же количество тепла за время Т выделяет постоянный ток некоторой величины I. Так что 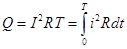; Þ 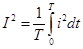. (20.7)

Подставив сюда i = i_asinwt и приняв во внимание, что sin²wt = (1 – cos2wt)ç2, получаем: 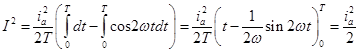. Отсюда 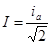. (20.8, 9)

Наряду с эффективным значением тока используется понятие среднего тока. Постоянный ток i_ср переносит за половину периода такой же заряд q, как и данный переменный. 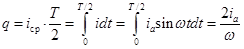. Отсюда 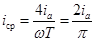. (20.10, 11)

Математически эффективный ток есть среднеквадратичный, а средний ток – среднеарифметический по модулю. Выразив из полученных формул амплитудный ток i_a, найдём связь между эффективным и средним токами.

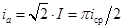, Þ 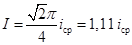. (20.12)

4. Сопротивление, индуктивность и ёмкость в цепи переменного тока:

а. Цепь с активным сопротивлением R, то есть с таким сопротивлением, которое обусловлено рассеянием электронов на узлах кристаллической решётки проводника. Индуктивность и ёмкость активного сопротивления равны нулю.

Пусть в цепи (рис.131) действует внешняя синусоидальная ЭДС E =E_аsinwt. В случае квазистационарного тока в любой момент времени для контура справедливо 2-е правило Кирхгофа.

iR =E_asinwt, Þ 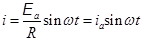. (20.13)

Ток через активное сопротивление R совпадает по фазе с ЭДС. Так как напряжение на сопротивлении равно ЭДС, то можно сказать, что изменения тока и напряжения на активном сопротивлении совпадают по фазе (рис.132).

б. Цепь с конденсатором, ёмкость которого С (рис.133). При условии квазистационарности 2-е правило Кирхгофа запишется так:

iR + u_C =E.. Но R = 0, следовательно, u_C =E.

Здесь u_C – напряжение на обкладках конденсатора.

Так как u_C= qçC, где q – заряд на обкладках конденсатора, то получаем: 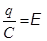, или q =E_aC×sinwt. Продифференцировав по времени t, получаем ток в цепи с ёмкостью.

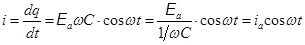. (20.14)

Выражение 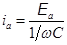есть амплитудный ток. Величину 1çwС = X_C формально можно рассматривать как сопротивление конденсатора переменному току. Его называют ёмкостным сопротивлением. Оно тем меньше, чем больше ёмкость конденсатора С и частота переменного тока w.

Так как coswt = sin(wt + pç2), то, сравнив напряжение на конденсаторе u_C =E =E_asinwt с током i = i_asin(wt + pç2), видим, что ток в цепи опережает напряжение на конденсаторе на четверть периода (рис.134).

Если сместить на графике начало координат на pç2 влево, для чего из аргументов функции надо вычесть pç2, то выражения для тока и напряжения принимают вид:

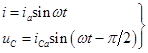. (20.15)

в. Цепь с катушкой, индуктивность которой L (рис.135). Полагаем, что активное сопротивление и ёмкость катушки равны нулю.

В контуре действуют две ЭДС: внешняя гармоническая E =E_аsinwt и ЭДС индукции, противодействующая направлению изменения внешней. По 2-му правилу Кирхгофа их сумма в любой момент времени равна нулю, так как R = 0. 0 =E_аsinwt – L 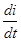. (20.16)

Чтобы выразить зависимость i(t), разделяем переменные и интегрируем. di = 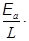sinwtdt, i = - 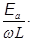coswt + i₀. (20.17)

Постоянную интегрирования i₀ отбрасываем, так как это составляющая постоянного тока через катушку и в данном исследовании не представляет интереса. Так как -coswt = sin(wt - pç2),

то i = 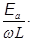sin(wt - pç2) = i_asin(wt - pç2). (20.18)

Величина wL = X_L имеет смысл индуктивного сопротивления цепи. Оно тем больше, чем больше частота w и индуктивность цепи L. Напряжение на зажимах индуктивности совпадает с внешней ЭДС. u_L =E_аsinwt = u_Lasinwt. Поэтому ток в цепи с индуктивностью отстаёт от напряжения на индуктивном сопротивлении на четверть периода (рис.136). Если сместить на графике рис.136 начало координат на pç2, то выражения для тока и напряжения на индуктивности принимают вид: 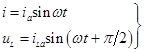. (20.19)

5. Выражения формул через синус и косинус. Часто ток и напряжение удобно выражать через функцию косинуса. Фазовый сдвиг между током и напряжениями на элементах цепи остаётся прежним, а сам переход от функции синуса к функции косинуса графически соответствует переносу начала координат по оси аргументов на pç2 вправо.

Ниже в левом столбце записаны формулы через синус, в правом – через косинус.

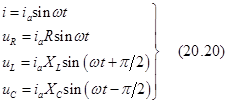
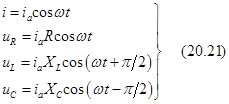
Здесь X_L = w L, X_C = 1çwС.

6. Векторные диаграммы. Хотя ток и напряжение физически являются скалярными величинами, для удобства анализа цепей переменного тока их можно рассматривать как векторы, только в комплексной плоскости. Сдвиг по фазе между током и напряжением в этом случае будет проявляться в разной ориентации векторов.

Если договориться ориентировать вектор тока в момент времени t = 0 вдоль действительной оси ОХ, то в рассмотренных случаях векторы напряжения ориентируются по разному.

а. Цепь с активным сопротивлением(рис.137). Векторная диаграмма в момент времени t = 0 представляет собой два сонаправленных вектора с модулями i_a и U_a = i_aR, ориентированных вдоль оси ОХ.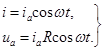

С течением времени оба вектора поворачиваются отно-сительно центра точки О как одно целое с угловой скоростью w. Через 1ç8 периода диаграмма принимает вид, указанный на рис.138.

Ток и напряжение на активном сопротивлении определяются во все моменты времени как проекция амплитудных векторов i_a и u_a на действительную ось ОХ.

б.Цепь с ёмкостью С. Угол между векторами i_a и u_Cа составляет 90° и остаётся неизменным во времени. Оба вектора поворачиваются как одно целое (рис.139).

Напряжение на конденсаторе, как и ток, в любой момент времени определяются проекцией амплитудных векторов на действительную ось ОХ. В момент времени t = 0 i = i_a, u_C = 0, при t = Tç8 i = i_acospç4, u_C = u_Cacos(-pç4).

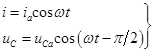
в. Цепь с индуктивностью L (рис.140). i = i_acoswt, u_L = i_aX_Lcos(wt + pç2). Напряжение на индуктивности опережает ток по фазе на pç2.

В момент времени t = 0 i = i_a, u = 0. В момент времени t = Tç8 i = i_acospç4, u_L = u_Lacos3pç4.

Итак, гармоническое изменение токов и напряжений формально можно изображать вращением векторных диаграмм как единого целого вокруг начала координат с угловой скоростью w. Мгновенные значения токов и напряжений в случае, когда они выражены через косинус, определяются проекцией концов соответствующих амплитудных векторов на действительную ось ОХ.

7. Закон Ома в цепи переменного тока. Рассмотрим цепь, включающую в себя активное сопротивление, ёмкость и индуктивность (рис.141). Если ток квазистационарный, то в любой момент времени его величина одинакова во всех точках цепи и равна i = i_acoswt. Напряжение на каждом элементе цепи соответственно равно u_R = i_aRcoswt, u_C = i_aX_Ccos(wt - pç2), u_L = i_aX_Lcos(wt + pç2). Как правило, диаграммы изображаются в тот момент времени, когда i = i_a (рис.142).

Каждый вектор амплитудного напряжения можно представить как произведение действительного числа i_a на векторы R, X_C, X_L, имеющие смысл сопротивлений элементов цепи переменному току. Поэтому для вычисления полного сопротивления цепи нужно найти векторную сумму сопротивлений всех элементов цепи, соединённых последовательно (рис.143). Модуль полного сопротивления Z равен 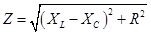. (20.22)

Модуль разности |X_L - X_C| называют реактивным сопротивлением цепи. Элементы цепи, обладающие только активным сопротивлением R, называются резисторами.

Умножив диаграмму сопротивлений (рис.143) на скалярную величину амплитудного тока i_a, получаем диаграмму напряжений (рис.144).

Угол j определяет сдвиг по фазе между током в цепи i и приложенным к ней напряжением u. Между величинами амплитудного тока i_a и амплитудного напряжения u_a существует постоянная связь. 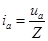. (20.23)

Разделив это выражение на 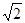, получаем: 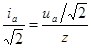. (20.23)

Но 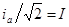- эффективный ток. Если ввести по формальной аналогии понятие эффективного напряжения 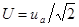, то получаем: 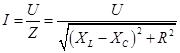. Закон Ома для цепи переменного тока. (20.24)

Эффективный ток, протекающий по участку цепи, пропорционален эффективному напряжению, приложенному к этому участку, и обратно пропорционален полному сопротивлению цепи.

8. Резонанс напряжений (рис.145). При последовательном включении индуктивного и ёмкостного сопротивлений могут возникать ситуации, когда их суммарное реактивное сопротивление обращается в нуль, |X_L - X_C| = 0. Это бывает в том случае, когда индуктивное сопротивление X_L равно по величине ёмкостному сопротивлению X_C. В результате полное сопротивление цепи становится минимальным и равным активному сопротивлению R, а ток – максимальным.

Напряжение на индуктивности и ёмкости пропорциональны их реактивным сопротивлениям, U_L = IX_L , U_C = IX_C. Увеличивая индуктивность L и уменьшая ёмкость С так, чтобы всё время сохранялось равенство X_L = X_C,можно сделать напряжение на элементах цепи U_L и U_C больше приложенного к цепи внешнего напряжения U. Такая ситуация называется резонансном напряжений (рис.146).

Из условия X_L = X_C резонансная частота: 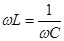, Þ 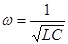. (20.25)

9. Резонанс токов. Рассмотрим случай когда в цепи есть такие точки ветвления, что индуктивность и ёмкость подключены к внешнему напряжению параллельно друг другу (рис.147).

Напряжение на индуктивности и ёмкости одинаковы, оно равно U_ab. Но ток через ёмкость опережает напряжение на pç2, а через индуктивность – отстаёт от напряжения на pç2. Поэтому токи в ветвях текут в противоположных направлениях, они сдвинуты по фазе друг относительно друга на p.

Чтобы вычислить полное сопротивление цепи между точками a и b, достаточно сложить их проводимости с учётом противоположных знаков (токи в ветвях колеблются в противофазе). 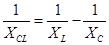, Þ 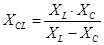. (20.26)

Здесь X_CL – реактивное сопротивление цепи между точками a и b.

Если X_C ® X_L, то знаменатель стремится к нулю, а сопротивление между точками a и b к бесконечности. Ток через резистор R в проводящих проводах стремится к нулю.

Но внутри цепи С-L конденсатор и катушка включены последовательно, их полное сопротивление при X_C ® X_L стремится к нулю. Поэтому внутри цепи С-L раскачиваются большие переменные токи. Возникает ситуация, называемая резонансом токов. Цепь из ёмкости и индуктивности называется колебательным контуром.

Как резонанс напряжений, так и резонанс токов наступают в случае, когда X_C = X_L , или wL = 1çwC. Отсюда следует, что для любой цепи переменного тока содержащей ёмкость и индуктивность, существует резонансная частота 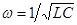. Период резонансных колебаний 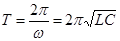. Формула Томсона (Кельвина), 1853. (20.27)

10. Мощность в цепи переменного тока. Мгновенное значение мощности в цепи переменного тока есть p = iu , где i и u – мгновенные ток и напряжение.

Пусть между током и напряжением есть сдвиг по фазе на угол j. Тогда

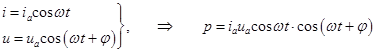. (20.28)

Среднее значение мощности переменного тока за период T найдётся интегрированием. 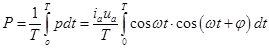. (20.29)

Так как cos(wt + j) = coswt cosj - sinwt sinj, а cos²wt = (1+cos2wt)ç2, то получаем:

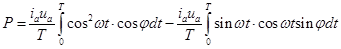. (20.30)

Cosj и sinj - постоянные для данной цепи числа и выносятся из под интеграла. Правый интеграл обращается в нуль, а левый от cos²wt распадается на два (сравните с вычислениями в п.3 наст. параграфа). 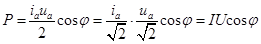. (20.31)

Здесь I и U – эффективные ток и напряжение.

Величина cosj называется коэффициентом мощности. Чем больше косинус фи, тем меньше бесполезные потери в цепи переменного тока.

Формула (22.31) определяет активную мощность, которая характеризует скорость необратимого превращения электрической энергии в другие виды энергии.

Произведения эффективных тока и напряжения называют полной мощностью и обозначают S.

I×U = S, P = S×cosj. (20.32)

Выражение Q = IUsinj = S×sinj (20.33)

называют реактивной мощностью. Она характеризует скорость передачи энергии от источника тока к приёмнику и обратно.

Величины P, S, Q образуют в комплексной плоскости треугольник мощностей, показанный на рис.148 для цепи с преобладанием индуктивности.

На рис.149 изображен треугольник мощностей для цепи с преобладанием ёмкости. Очевидно, S = I²Z, P = I²R, Q = I²|X_L -X_C|.

Единица активной мощности P – ватт (Вт), единица полной мощности S – вольт-ампер (В×А), единица реактивной мощности Q – вольт-ампер-реактивный (вар).

Реактивная мощность, потребляемая в электрических цепях, вызывает дополнительные активные потери в подводящих проводах. Для устранения перегрузок и повышения коэффициента мощности делают компенсацию реактивных нагрузок, максимально приближая X_L к X_C.

Амперметры и вольтметры в цепях переменного тока проградуированы на эффективные ток и напряжение. Поэтому произведение показаний амперметра и вольтметра, подключённых к нагрузке, даёт полную мощность S, потребляемую данной нагрузкой. Для измерения активной мощности применяются специально сконструированные ваттметры (Описание ваттметров см. в лабораторном практикуме по электричеству).