Электромагнитные волны

1. Волны вдоль проводов. Любой участок двухпроводной линии обладает некоторой ёмкостью и индуктивностью. Поэтому любой участок такой линии обладает свойствами колебательного контура, а вся линия в целом может рассматриваться как система связанных колебательных контуров (рис.161).

Системы, подобные двухпроводной линии, называются распределёнными.

Пусть в какой-то точке бесконечной двухпроводной линии действует переменная гармоническая ЭДС. В результате по линии протекает переменный ток. Если скорость изменения ЭДС достаточно велика, то токи проводимости в проводах будут замыкаться токами смещения между ними (рис.162).

Но согласно первому уравнению Максвелла (Ф.19.3) эти токи смещения, то есть изменяющееся эл. поле E, вызывают появление магнитного поля B. Так как электрическое поле распространяется в проводнике с некоторой скоростью, то в рамках грубой наглядности можно сказать, что увеличивающаяся ЭДС на зажимах a и b вызывает появление первого токового кольца 1, а это токовое кольцо, согласно второму уравнению Максвелла (Ф.19.4) создаёт магнитное кольцо А. Это магнитное кольцо А создаёт, в свою очередь, новое вихревое кольцо электрического поля 2, а то – новое магнитное кольцо Б, и так далее. Каждый раз при создании нового кольца происходит уничтожение предыдущего. В результате вдоль проводов бежит импульс электромагнитной волны, несущий информацию о величине и направлении той ЭДС, которая была на зажимах а – b в момент начала движения импульса.

Изменение электрического и магнитного полей в каждой точке пространства в любой момент времени совпадают по фазе между собой. Векторы E и B нормальны друг к другу и изменяются по гармоническому закону (рис.163).

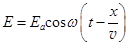, (22.1)

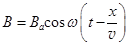. (22.1)

Здесь v – фазовая скорость волны. Векторы E, B и v образуют правовращательную тройку векторов.

При малых частотах ω перенос электрического поля происходит, в основном, с помощью токов проводимости по проводам. Если же ω велика, то роль токов проводимости снижается, а перенос электрического поля происходит за счёт токов смещения. Электрические явления в этом случае в значительной степени определяются электромагнитными волнами.

При достаточно больших ω провода можно вообще убрать, электрическое поле будет распространяться в диэлектрической среде в виде электромагнитных волн.

2. Скин – эффект. (skin по англ. – кожа). Состоит в том, что быстропеременные токи текут по поверхности проводника, быстро уменьшаясь с глубиной.

Если по проводнику течёт постоянный ток, то его плотность во всех точках сечения проводника примерно одинакова.

На каждый заряд действует сила Лоренца, стремящаяся сместить его к центру провода (рис.164). При обычных токах в металлических проводниках эта сила невелика и не оказывает заметного влияния на плотность тока. И лишь при сильных разрядах в плазме эта сила приводит к сжатию плазменного шнура (пинч-эффект).

Если ток в проводе переменный, то он генерирует переменное магнитное поле, а оно, в свою очередь, генерирует переменное вихревое электрическое поле. Рассмотрим механизм скин-эффекта при нарастании и убывании тока.

а. Ток нарастает. Нарастающая индукция магнитного поля B вызывает появление вихревого электрического поля E, которое у поверхности проводника направлено по току, а на оси проводника – противоположно току. В результате у поверхности ток усиливается, а центре – ослабляется (рис.165).

б. Ток убывает. В этом случае ослабевающая индукция B вызывает электрическое поле E, направленное противоположно первому случаю, то есть на оси – по току, а на поверхности – против тока (рис.166).

В обоих случаях вихревое эл. поле на оси проводника препятствует, а на поверхности – способствует изменениям тока. Поэтому на оси проводника переменный ток слабее, на поверхности – сильнее.

Амплитуды векторов E и B затухают с глубиной по экспоненциальному закону:

E = E₀exp(-αx), В = В₀ exp(-αx). (22.3)

Здесь E₀ и В₀ – амплитудные векторы на поверхности проводника, x – глубина, отсчитываемая с поверхности, α – коэффициент затухания, 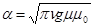, где ν – частота тока, g – удельная электропроводность проводника.

Чем больше частота тока ν, магнитная проницаемость проводника μ и его электропроводность g, тем больше затухание. С увеличением частоты ν толщина поверхностного слоя, по которому проходит ток, уменьшается. В результате сопротивление проводника возрастает. Поэтому с ростом ν роль токов проводимости уменьшается, а токов смещения – увеличивается.

Величина, обратная коэффициенту затухания, 1çα = δ есть глубина уменьшения амплитуды в е раз. При ν = 50 Гц для меди δ = 0,74 мм. Отсюда понятно, что линии многоканальной связи, работающей на ТВЧ, могут использовать не дешёвые стальные провода, а дорогие медные. Увеличение числа каналов линии связи требует увеличения частоты тока, а это приводит к недопустимо большому затуханию и в медных проводах. Практический путь к повышению пропускной способности линий связи состоит в замене металлических проводов оптическими световодами, позволяющими использовать для передачи информации электромагнитные волны сверхвысокой частоты.

3. Стоячие волны. Если проводящая линия ограничена в пространстве, то на её концах происходит отражение электромагнитных волн. При сложении отражённых и прямых волн возникают стоячие электромагнитные волны, в которых изменение величин Е и В уже не совпадает по фазе, поскольку при отражении одна из величин Е или В – обязательно меняет знак. В стоячей электромагнитной волне узлы электрического поля совпадают с пучностями магнитного поля, и наоборот (рис.167).

Условие существования стоячих волн: 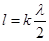, (22.4)

где l – длина линии, λ – длина электромагнитной волны, k = 1,2,3,… - натуральное число.

Если измерить λ, то, зная частоту генератора ν, из условия υ = λν можно найти экспериментально скорость распространения электромагнитных волн.

4. Опыты Герца. В 1888-89 годах Генрих Герц выполнил серию экспериментов, в которых убедительно доказал справедливость электромагнитной теории Максвелла. Генератор электромагнитных колебаний был искровой колебательный контур.

Опыты Герца по созданию электромагнитных колебаний с помощью вибраторов и по приёму этих колебаний на расстоянии в пределах лабораторной комнаты с помощью резонаторов показали, что от вибратора распространяется ЭМ-волна, способная отражаться от металлической поверхности и возбуждающая в приёмной антенне–резонаторе – токи той же частоты, что и колебания в вибраторе (рис.168).

Герц показал, что электромагнитная волна поляризуется и интерферирует, а проходя через границы раздела разных диэлектрических сред преломляется в соответствии с законами оптики.

Все открытые явления полностью укладывались в рамки теории Максвелла и тем самым подтвердили её.

5. Скорость распространения электромагнитных волн находится из системы уравнений Максвелла. Впервые эту работу выполнил Максвелл, получивший для скорости v ЭМ-волны выражение: 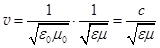. Закон Максвелла (22.5)

Здесь 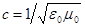- скорость света (ЭМ-волны) в вакууме.

Поскольку ε > 1, а μ даже для наиболее сильных диамагнетиков очень мало отличается от единицы, то в целом произведение ε μ > 1. Это значит, что скорость распространения ЭМ-волн в веществе всегда меньше скорости в вакууме v < c и зависит практически лишь от диэлектрических свойств среды.

Величину 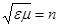называют показателем преломления среды. В оптике закон Максвелла обычно записывают в виде: 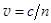. У всех сред n > 1, в вакууме n = 1. (22.6)

Электромагнитные волны представляют собой полевую форму материи, так называемое поле излучения. Поле излучения в отличие от других форм материи не может находиться в состоянии покоя. Оно всегда движения, причём скорость его в пустоте не зависит от выбора системы отсчёта и может принимать лишь одно значение c » 3·10⁸ м/с.

6. Дисперсия волн. Материальные параметры ε и μ являются константами лишь в случае статических полей или в случае, когда поле изменяется очень медленно. Если же поле изменяется быстро, так что время его изменения сравнимо с временем релаксации τ электрического молекулярного диполя (или элементарного магнитного диполя), то параметры ε и μ сложным образом зависит от частоты колебаний поля ν. В результате и скорость распространения электромагнитных волн в веществе зависит от частоты n.

Явление зависимости скорости распространения волны от частоты (или длины волны), называется дисперсией.

Если источник излучает электромагнитные волны разных частот, то эти волны распространяются в веществе с разными скоростями. При прохождении границы раздела сред с разными ε (величина μ практически не влияет), электромагнитные волны в зависимости от скорости v, а, следовательно, в зависимости от частоты ν преломляются на разные углы. В результате плоско-параллельный пучок, состоящий из смеси волн разных частот, диспергирует, то есть расщепляется в веер лучей (рис.169).

Наиболее заметно дисперсия проявляется в электромагнитных волнах высоких частот, включая диапазон частот видимого света. Поэтому законы взаимодействия электромагнитных волн с веществом изучаются, как правило, в оптике. Скорость распространения волн в радиодиапазоне может быть установлена экспериментально путём измерения расстояний между узлами или пучностями стоячих волн известной частоты на вибраторах.

7. Перенос энергии и импульса в ЭМ-волне. Электромагнитные волны, как и любой волновой процесс, переносят в пространстве энергию.

В случае упругих волн эта энергия слагается из потенциальной энергии деформации среды и кинетической энергии движения её частиц. Энергия же электромагнитных волн слагается в любой момент времени из энергии взаимосвязанных электрического и магнитного полей.

Энергия, переносимая электромагнитными волнами, как и в механике, определяется вектором плотности потока энергии S, то есть количеством энергии, которое переносится волновым процессом через единичную площадку σ, ориентированную перпендикулярно вектору скорости движения волнового фронта v в данный момент времени (рис.170), 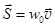. (22.7)

Здесь w₀ – плотность энергии ЭМ-поля. Так как

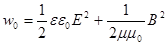, то 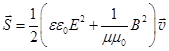. (22.8)

Вектор S можно представить через характеристики ЭМ-поля E и B. Как и в колебательном контуре средние энергии электрического и магнитного полей в ЭМ-волне одинаковы. Но поскольку оба поля Е и В изменяются в одной фазе, то одинаковы и мгновенные значения плотности энергии, то есть εε₀E² = B²çμμ₀. Если с учётом этого обстоятельства преобразовать выражение (22.8) (см., например, [1], §240, с.529), то для вектора S получается выражение: 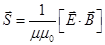. Вектор Пойнтинга 1883, (22.9)

Электромагнитное поле обладает не только энергией, но массой и импульсом. Из формулы Эйнштейна W = mc² = w₀V, где V – объём, получаем пространственную плотность распределения массы поля: 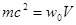Þ 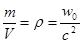. (22.10)

Импульс единичного объёма электромагнитной волны есть 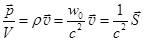. (22.11)

8. Поток энергии ЭМ-поля в проводнике. Найдём поток электромагнитной энергии, втекающий в единичный объём длинного цилиндрического провода, по которому протекает электрический ток i.

Вектор Пойнтинга 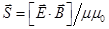на поверхности цилиндрического провода направлен по радиусу (рис.171). Поэтому его поток через основание цилиндра равен нулю, а через боковую поверхность есть 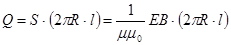. (22.10)

Из закона Ома j = gE Þ E = jçg, где j – плотность тока в проводнике, g – удельная электропроводность проводника. Индукция магнитного поля на поверхности длинного цилиндрического провода есть 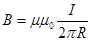(формула 13.8) (22.11)

Ток, текущий по проводу, I = j×pR². Объём провода V = pR²l. Отсюда

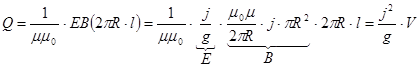. (22.12)

Поток энергии в единичный объём проводника 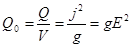(22.13)

оказался в точности равен тепловой энергии, выделяющейся в единичном объёме проводника в соответствии с законом Джоуля-Ленца.

Итак, энергия,идущая на нагрев проводника, поступает в него через боковую поверхность в виде энергии электромагнитного поля из окружающего проводник пространства, а не вдоль оси провода, как это кажется на первый взгляд. В это пространство она поступает из тех участков цепи, где действует ЭДС источников тока.

9. Излучение элементарного диполя. Заряд, движущийся в проводнике с постоянной скоростью, создаёт постоянное магнитное поле B. Это поле имеет постоянное во времени значение во всех точках пространства. Вдоль прямой, по которой движется заряд, магнитное поле равно нулю. (См. магнитное поле элемента тока, §12, п.6).

Для того, чтобы заряд излучал, он должен двигаться ускоренно. Это ускоренное движение можно реализовать с помощью элементарного диполя. В отличие от рассмотренного в п.3 макродиполя, длина которого l соизмерима с длиной волны l и связана с ней соотношением l = kl / 2, где k = 1,2,3,…, длина элементарного диоля много меньше длины излучаемой им волны, l << l.

Примером элементарного диполя являются два металлических шара, заряжаемые от какого-либо генератора электрических колебаний (рис.172). Если генератор создаёт гармоническую ЭДС, то заряд на шарах изменяется также по гармоническому закону, q = q₀sinwt, (22.14)

и между шарами протекает переменный ток

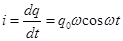. (22.15)

Этот переменный ток представляет собой ускоренное движение зарядов вдоль оси ОY, поэтому в пространстве вокруг оси OY излучается электромагнитная волна.

Если расстояние r от диполя много больше длины l, то волновые поверхности приобретают форму сферы, сечение которой вдоль оси диполя показано на рис.173. Замкнутые кривые здесь представляют собой силовые линии вихревого электрического поля Е. Расстояние между соответственными точками таких замкнутых фигур вдоль по радиусу равно l/2.

Важнейшим примером элементарных диполей являются электроны внутри атомов. Круговое движение электронов можно разложить на два взаимно перпендикулярные линейные гармонические колебания, каждый из которых представляет элементарный диполь.