Поле в магнетиках. Диамагнетизм
1. Магнетики. Магнитная проницаемость. Магнетиком называют любое вещество в магнитном поле. Сила взаимодействия между элементарными токами dF, определяемая законом Ампера (12.6), зависит от того, в каком веществе находится взаимодействующие токи. Её силу можно представить так: dF = mdF0. (17.1)
где dF0 - сила взаимодействия между этими токами в вакууме. Некоторые вещества уменьшают силу взаимодействия токов по сравнению с вакуумом, другие – увеличивают.
Безразмерное число μ, показывающее во сколько раз сила взаимодействия между токами в веществе больше силы взаимодействия в вакууме, называют магнитной проницаемостью вещества.
Магнитная проницаемость μ – всегда положительное число, больше или меньше 1. Она входит в формулы законов Ампера, Био-Савара-Лапласа, электромагнитной индукции и в их многочисленные следствия.
2. Вектор намагниченности. Магнитная восприимчивость. Магнитные свойства тел обусловлены движением электрических зарядов в атомах и молекулах. Любой движущийся в оболочке атома электрон в магнитном отношении эквивалентен элементарному контуру с током, имеющему определённый магнитный момент, называемый орбитальным.
Кроме того, каждый электрон имеет собственный магнитный момент, называемый спиновым. Спиновый момент в начале связывался с предполагаемым вращением электрона вокруг своей оси. Когда позднее выяснилось, что эта наглядная модель неприменима, спиновый момент стали просто полагать определённым качеством электрона, таким как масса и заряд. Магнитный момент атома слагается из орбитальных и спиновых магнитных моментов всех его электронов и магнитного момента ядра.
Полный магнитный момент единицы объёма вещества называют вектором намагничения вещества и обозначают J, Он равен сумме магнитных моментов всех частиц в единице объёма. В несильных полях вектор намагничения пропорционален индукции магнитного поля, 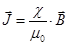 . (17.2)
. (17.2)
Магнитная постоянная μ0 введена здесь для уравнивания размерностей так, чтобы коэффициент пропорциональности χ был безразмерным числом. Величину χ называют магнитной восприимчивостью вещества. Между μ и χ линейная связь: μ = χ + 1. (17.3)
Магнитная восприимчивость χ может быть как положительным, так и отрицательным числом. В зависимости от значений χ и μ все материалы делятся на три большие группы:
χ < 0, μ < 1 – диамагнетики;
χ > 0, μ > 1 – парамагнетики;
χ >> 0, μ >> 1 – ферромагнетики.
3. Диамагнетики – это вещества, магнитный момент атомов которых в отсутствие внешнего магнитного поля равен нулю. К диамагнетикам относятся все инертные газы, металлы Cu, Ag, Au, Pb, Hg, Zn, а также Sb, I (йод), C, Si, S, H2O, N2, Сo2 и большинство органических соединений.
При внесении диамагнетика во внешнее поле суммарный магнитный момент каждого атома становится отличным от нуля и направленным против внешнего поля. Всё вещество в целом приобретает направленный против поля магнитный момент. В результате магнитное поле в веществе диамагнетика ослабляется, а сам диамагнетик выталкивается из поля.
4. Механизм ослабления магнитного поля в диамагнетиках объяснил в 1903 – 905 г.г. Поль Ланжевен. В то время ещё не были разработаны динамические модели атома Бора и Резерфорда. Было известно лишь, что в состав наружной оболочки атомов входит электрон – частица, хорошо изученная в опытах с катодными лучами и с фотоэффектом. Поэтому в основу своих рассуждений Ланжевен положил гипотезу Ампера о молекулярных круговых токах.
Атом в теории Ланжевена представляет собой положительно заряженное ядро, вокруг которого по круговым траекториям движутся электроны. Объяснение Ланжевена сделано в рамках классической электронной теории. То есть он полагал, что электроны подчиняются законам Ньютона, а их энергия может изменяться непрерывно.
Рассмотрим состояние отдельного электрона в атоме, когда внешнего магнитного поля нет, и состояние, когда внешнее поле есть. Полагаем, что движение электронов в атоме не связаны между собой.
а. Поля нет, B = 0. Полагаем, что рассматриваемый электрон движется во внешней оболочке вокруг центрально-симметричного иона. В отсутствие внешнего поля уравнение движения его имеет вид: 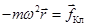 . (17.4)
. (17.4)
Здесь m – масса электрона, ω – угловая скорость его обращения вокруг иона, fКл - кулоновская сила притяжения электрона к положительному иону (рис.120-а).
Магнитный момент диамагнитных атомов в отсутствие внешнего поля равен нулю. Но это значит, что орбитальный магнитный момент электрона рmе равен по величине противоположно направленному магнитному моменту иона рmи.
(Спиновые магнитные моменты здесь не принимаются во внимание. Это не влияет на строгость рассуждений, поскольку при включении поля В они не меняются).
б. Внешнее поле В рmе. При включении внешнего магнитного поля В на электрон кроме кулоновской будет действовать ещё магнитная составляющая силы Лоренца fm. Если вектор B сонаправлен с орбитальным моментом электрона рmе (рис.120-б), то сила fm направлена по радиусу вращения в сторону, противоположную кулоновской силе. Угловая скорость обращения электрона изменяется на величину Dw, а уравнение движения принимает вид: - m(w + Dw)2r= fКл + fm. (17.5)
Вычтем из (17.4) уравнение (17.5) - mw2r + mw2r + 2mwDw r + mw(Dw)2r= - fm. (17.6)
Пренебрегаем членом, содержащим (Dw)2. Спроектировав уравнение (17.6) на радиус-вектор r и приняв во внимание, что вектор B перпендикулярен плоскости вращения электрона, получаем: 2m(w r)Dw = - evB. Так как ω r = v, то 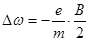 . (17.7)
. (17.7)
 |
Здесь e – заряд движущегося вокруг иона электрона, в данной формуле – положительное число. При заранее заданном направлении орбитального момента рmе относительно магнитного поля B изменение знака заряда e орбитальной частицы компенсируется изменением направления её движения и не влияет на направление силы Лоренца.
Итак, при В рmе электрон тормозится, его частота обращения уменьшается, уменьшается и орбитальный момент рmе. Равновесие между орбитальным моментом рmе и моментом иона рmи нарушается. Момент иона становится больше, чем орбитальный момент электрона. Диамагнитный атом приобретает во внешнем поле магнитный момент, направленный против внешнего поля B. В результате поле в диамагнетике ослабляется.
в. Поле В¯рmе (рис.120-в). В этом случае сила Лоренца меняет направление, её проекция на радиус становится отрицательной. Поэтому вместо - evB в формуле (17.7) получается + evB, и выражение частоты принимает вид: Dw = - eBç2m. (17.8)
Здесь все величины – положительные числа.
Частота обращения электрона в этом случае увеличивается, орбитальный магнитный момент электрона рmе становится больше по величине магнитного момента иона рmи. В результате диамагнитный атом приобретает магнитный момент, и в этом случае направленный против поля В. Поле В ослабляется.
Заметим, что в первом случае, когда Врmе, атом находится в устойчивом равновесии. Во втором случае, когда В¯рmе, равновесие неустойчиво, вероятность его реализации ничтожна.
5. Относительное изменение орбитального магнитного момента электрона Dрmеçрmе можно найти, используя формулу момента кругового тока (13.14). Если электрон совершает вокруг ядра в единицу времени ν = ωç2π оборотов, то это равносильно тому, что по орбите как по проводнику идёт ток i = eν = eωç2π. Тогда 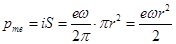 . (17.9)
. (17.9)
Здесь r – радиус орбиты электрона. Изменение орбитального момента электрона обусловлено изменением угловой скорости его обращения, 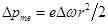 . (17.10)
. (17.10)
Относительное изменение момента равно 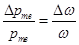 . (17.11)
. (17.11)
Скорость обращения электрона ω в невозмущённом атоме найдётся из уравнения (17.4). Полагая заряд иона + e, спроектировав уравнение на радиус и подставив в него выражение кулоновской силы fКл = e2ç4πε0r2,получаем: 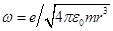 . (17.12)
. (17.12)
Изменение скорости Δω по величине определяется формулой (17.8). Подставляем (17.8) и (17.12) в формулу (17.11). 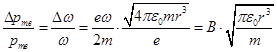 . (17.13)
. (17.13)
Поля, создаваемые обычными электромагнитами, достигают B = 1 Tл. Радиус атомов r ≈ 10-10 м, масса электрона m ≈ 10-30 кг. 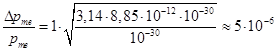 .
.
 6. Ларморовская прецессия электронных орбит. Рассмотренные в п.4 случаи, когда векторы В и рmе параллельны или антипараллельны, являются идеализациями. В действительности ориентация атомов в газах, жидкостях, в поликристаллах носит случайный характер. Поэтому угол a между векторами B и рmе заключён в интервале от 0 до p.
6. Ларморовская прецессия электронных орбит. Рассмотренные в п.4 случаи, когда векторы В и рmе параллельны или антипараллельны, являются идеализациями. В действительности ориентация атомов в газах, жидкостях, в поликристаллах носит случайный характер. Поэтому угол a между векторами B и рmе заключён в интервале от 0 до p.
Действующее на элементарный круговой ток однородное магнитное поле B создаёт пару сил с моментом 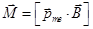 (См. §14, п.2, формула 14.4).
(См. §14, п.2, формула 14.4).
Движущиеся по круговой орбите электрон обладает механическим моментом (импульса) L = mυr . Поэтому электронная орбита представляет собой гироскоп. Под действием момента пары сил M гироскоп прецессирует с угловой скоростью Ω вокруг оси OZ, параллельной полю B (рис.121).
Найдём угловую скорость прецессии Ω. Для этого рассмотрим силы, действующие на электрон в неинерциальной системе отсчёта, связанной с орбитой и равномерно вращающейся с угловой скоростью Ω вокруг оси OZ инерциальной системы, связанной с магнитным полем B.
Кулоновская сила fКл, удерживающая электрон на круговой орбите, действуют внутри атома и не влияет на прецессионное движение электрона.
Прецессию создают действующие на электрон внешние силы. Это сила Лоренца 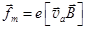 и две силы инерции: сила Кориолиса
и две силы инерции: сила Кориолиса 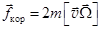 и центробежная сила инерции
и центробежная сила инерции 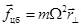 .
.
Здесь va - скорость движения электрона относительно магнитного поля B. То есть это скорость в ИСО. Она равна сумме относительной v (скорости движения электрона в атоме) и переносной 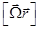 (скорости, обусловленной прецессией атома),
(скорости, обусловленной прецессией атома), 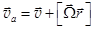 .
.
Логично полагать, что угловая скорость прецессии Ω – величина того же порядка, что и изменение скорости Δω, найденное в п.4. То есть эта величина на 5-6 порядков меньше величины ω. Но это значит, что и переносная скорость 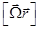 . На несколько порядков меньше скорости v электрона в атоме. Поэтому пренебрежём переносной скоростью и будем полагать va = v. Из-за малости Ω пренебрежём так же членом, содержащим Ω2, то есть центробежной силой инерции
. На несколько порядков меньше скорости v электрона в атоме. Поэтому пренебрежём переносной скоростью и будем полагать va = v. Из-за малости Ω пренебрежём так же членом, содержащим Ω2, то есть центробежной силой инерции 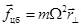 .
.
В результате кроме внутренней кулоновской силы, удерживающей электрон на окружности, на него действуют ещё две внешние – сила Кориолиса fкор и сила Лоренца fm. Обе эти силы лежат на радиусе r^, перпендикулярном к оси OZ.
При равномерном вращении НИСО сумма этих сил равна нулю.
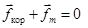 ,
, 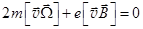 . (17.14)
. (17.14)
Отсюда 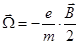 . (17.15)
. (17.15)
Заряд электрона e здесь – отрицательное число. Его магнитный момент рmе противоположен механическому моменту импульса 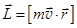 (рис.121). Взаимная ориентация векторов рmе и L меняется при смене знака орбитальной частицы.
(рис.121). Взаимная ориентация векторов рmе и L меняется при смене знака орбитальной частицы.
Формула (17.15) определяет угловую скорость прецессии электронной орбиты в магнитном поле. Эта ларморовская прецессия определяет реальный диамагнетизм, присущий атомам всех химических элементов.
При включении магнитного поля внутреннее состояние электрона на орбите не меняется. Это значит, что не меняется частота ω его обращения. Просто орбита электрона начинает прецессировать вокруг оси OZ, параллельной линиям B, с угловой скоростью W.
 Полученное в пункте 4 формальное изменение частоты обращения электрона Δω можно толковать как результат наложения на обращение электрона, происходящее с частотой ω, ларморовской прецессии его орбиты с частотой Δω = Ω.
Полученное в пункте 4 формальное изменение частоты обращения электрона Δω можно толковать как результат наложения на обращение электрона, происходящее с частотой ω, ларморовской прецессии его орбиты с частотой Δω = Ω.
7. Магнитная восприимчивость диамагнетиков. Магнитный момент атомов диамагнетиков появляется лишь при включении внешнего поля B. Он равен сумме изменений орбитальных моментов электронов, обусловленных прецессией их орбит.
Чем меньше угол α между вектором B и вектором орбитального момента рmе, тем большую площадь в плоскости XOY, перпендикулярную B, ометает электрон при прецессии его орбиты, тем более абсолютная величина Dрmе.
На рис.122 показано сечение области, в которой находится прецессирующий электрон (Заштрихованное кольцо внизу рисунка). Расстояние электрона от оси OZ изменяется в пределах от rmin до rmax . Оно тем больше, чем меньше угол θ.
Изменение орбитального магнитного момента электрона равно произведению тока его прецессионного движения i = eΩç2π на площадь токового контура 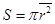 .
.
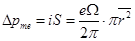 , или
, или 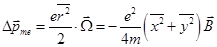 . (17.16)
. (17.16)
Допустим, что атом содержит z электронов, которые в своём движении не влияют друг на друга. Так как в диамагнетике в отсутствие поля B 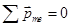 , то это значит, что расположение электронов в атоме симметрично. Их средние расстояния по осям одинаковы.
, то это значит, что расположение электронов в атоме симметрично. Их средние расстояния по осям одинаковы.
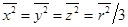 , Þ
, Þ 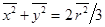 . (17.17)
. (17.17)
Подставляем в (17.16) и умножаем на число электронов z 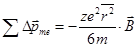 . (17.18)
. (17.18)
Если концентрация атомов n, то вектор намагничения 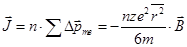 . (17.19)
. (17.19)
Так как n = rNAçM, где r - плотность вещества, М – его малярная масса, NA – число Авогадро, то окончательно поучаем: 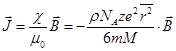 . (17.20)
. (17.20)
Отсюда получаем магнитную восприимчивость c вещества диамагнетика в классической теории Ланжевена. 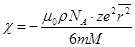 . (17.21)
. (17.21)
Таблица 17.1
| Вещество | Опыт | Теория | ||
| m | c, 10-6 | m | c , 10-6 | |
| Висмут Bi | 0,999824 | -176 | 0,999852 | -148 |
| Золото Au | 0,999961 | -39 | 0,999892 | -108 |
| Медь Cu | 0,999990 | -10 | 0,999954 | -46 |
| Свинец Pb | 0,999984 | -16 | 0,999905 | -95 |
| Серебро Ag | 0,999981 | -19 | 0,999933 | -67 |
В таблице 17.1 приведены значения величин m и c, полученные в опыте, и значения величин m и c, вычисленные по формуле (17.21) и (17.3).
Сравнение результатов показывает, что теория Ланжевена неплохо удовлетворяет эксперименту. Даже самые большие расхождения по величине c не превышают одного порядка. Что удивительно, если учесть множество нестрогостей в теории Ланжевена.
Заметим, что диамагнетизм – это проявление закона электромагнитной индукции. При включении магнитного поля возбуждающееся при нарастании индукции В вихревое электрическое поле совершает работу по генерации индукционного тока – прецессионного движения электронов. Согласно правилу Ленца направление индукционного тока таково, что его магнитное поле препятствует нарастанию внешнего поля В, то есть ослабляет его.
Внутриатомное движение электронов не затухает. Поэтому ослабление поля В сохраняется до тех пор, пока поле В не начнёт исчезать. Уменьшаясь, оно возбуждает вихревое электрическое поле, которое затормаживает прецессию электронов.
Дата добавления: 2018-05-10; просмотров: 2307;











