Гетерогенное (неравновесное) распределение микрокомпонента между твердой и жидкой фазами

Гетерогенное (неравновесное) распределение может быть до­стигнуто путем медленного испарения раствора, содержащего ма­кро- и микрокомпоненты, при непрерывном его перемешивании.

Этот случай был впервые рассмотрен Г. Дернером и В. Хоскинсом, которые в своих теоретических выводах исходили из кинетических представлений о ионном обмене между поверхно­стью кристалла и раствором, развитых Ф. Панетом.

Представим себе очень медленно растущий кристалл барие­вой соли, находящийся в ее насыщенном растворе, содержащем некоторое количество радия. В каждый данный момент роста между поверхностным слоем кристалла и раствором происходит ионный обмен, причем на поверхности кристалла наряду с ио­нами бария фиксируется также некоторое количество ионов ра­дия, пропорциональное концентрации их в растворе. Если про­цесс роста происходит достаточно медленно для того, чтобы ме­жду поверхностным слоем и раствором успевало установиться равновесие, то к распределению радия (в отношении каждого элементарного слоя кристалла) может быть приложено уравне­ние Бертло — Нернста — Хлопина:

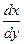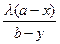= (5)

где dx — количество соли радия, перешедшей в элементарный слой кристаллов;

dy — количество соли бария, перешедшей в элементарный

слой кристаллов;

а и b — количества солей радия и бария в растворе в начале кристаллизации;

х и у — количества солей радия и бария, перешедших в дан­ный момент кристаллизации в смешанный кристалл;

λ — постоянная кристаллизации.

После того как закончится образование первого элементар­ного слоя, начнет образовываться другой. Между новым эле­ментарным слоем и раствором вновь установится истинное рав­новесие, так как обмен между отдельными слоями практически не происходит вследствие отсутствия диффузии и медленности процесса перекристаллизации. В этих, условиях распределение микрокомпонента (радия) в кристалле будет определяться прежде всего численным зна­чением постоянной кристаллизации А,.

В том случае, когда λ= 1 (распределение изотопов), концен­трация распределяющейся микропримеси будет одинакова для всех слоев, и мы получим однородный кристалл. В противном случае, когда λ ≠ 1, образующиеся кристаллы не будут однород­ными. Очевидно, что при λ > 1 концентрация микрокомпонента в поверхностном слое растущего кристалла будет максимальной в начале кристаллизации. Образующиеся в дальнейшем слои кристалла будут беднее микрокомпонентом, так как процесс кри­сталлизации приводит к постепенному обеднению им раствора/

Таким образом, при λ > 1 образуются слоистые кристаллы, содержание микрокомпонента в которых уменьшается в направ­лении от внутренних слоев к наружным.

Прямо противоположная картина распределения наблюдается в том случае, когда λ< 1. Нетрудно видеть, что получаемая при этом слоистая структура отличается от первой тем, что измене­ние концентрации микрокомпонента в элементарных слоях происходит в обратном направлении.

Неоднородность образующихся в этих случаях кристаллов может быть установлена с помощью радиографического иссле­дования или измерения активности растворов, получающихся при фракционированном растворении кристаллов.

Интегрируя выражение (5) можно получить уравнение, описывающее распределение микрокомпонента между всем кри­сталлом и раствором в определенный момент кристаллизации.

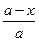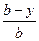1п = ln (6)

Таким образом, в противоположность ранее указанным трем путям изучения сокристаллизации, приводящим к гомоген­ному распределению, 4-й путь (медленное испарение насыщен­ного раствора при постоянной температуре и непрерывном пере­мешивании) приводит к гетерогенному распределению. При та­ком распределении логарифм .отношения количества (концентра­ции) микрокомпонента в растворе в данный момент к количе­ству его в начале кристаллизации, деленный на логарифм отно­шения количества макрокомпонента в данный момент к количе­ству его в начале кристаллизации, является постоянной вели­чиной ( ).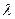

Если уравнение (1), являющееся математическим выра­жением закона Хлопина, требует наличия истинного равновесия между выделившимися кристаллами и раствором, а также рав­номерного распределения микрокомпонента по всему объему кристалла, то формула Дернера и Хоскинса относится к случаю, когда истинное равновесие между кристаллами и раствором не существует (здесь мы имеем дело с термодинамически неустой­чивым, как бы замороженным состоянием).