Гомогенное распределение микрокомпонента между твердой и жидкой фазами

Процессы изоморфной и изодиморфной сокристаллизации в зависимости от условий опыта могут приводить к гомогенному или гетерогенному распределению радиоактивного элемента между твердой и жидкой фазами. При этом гомогенным мы будем называть такое распределение, которое характеризуется установлением термодинамического равновесия между кристал­лом в целом и раствором.

Вопрос о распределении веществ, в частности электролитов,
между твердой фазой и раствором привлекал внимание хими­ков уже в 90-х годах прошлого столетия, когда были осуще­ствлены классические исследования Я. Вант-Гоффа и Б. Розебума. Теоретические работы этих ученых были посвящены
изучению твердых растворов и условий равновесия между сме­шанными кристаллами и растворами, из которых произошло ихвыделение. Применимость газовых законов к разбавленным растворам, не исключая и кристаллических растворов или изо­морфных смесей, открывала перед исследователями возмож­ность определять экспериментальным путем молекулярное со­стояние в твердых телах.

Распределение вещества между кристаллической и жидкой фазами должно происходить по закону, аналогичному тому, который управляет распределением вещества между газообраз­ной и жидкой фазами (закон Генри — Дальтона) и между двумя жидкими фазами (закон Бертло — Нернста), т. е. должно быть справедливым соотношение:

K_N = 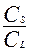(1)

где с_(S) и с_(L)—равновесные концентрации микрокомпонента в твердой и жидкой фазах; К_N — константа распределения (константа Нернста),

Очевидно, что закон распределения вещества между двумя фазами может быть справедливым в простой форме (1) при следующих условиях:

а) если имеет место истинное термодинамическое равновесие между кристаллами и раствором;

б) если процесс распределения происходит при неизменном составе фаз и постоянных внешних условиях (температура и давление); ,

в) если молекулярное состояние распределяющегося веще­ства в обеих фазах одинаково.

Однако, воз­можность распределения радиоактивных элементов в системах типа «раствор — твердая кристаллическая фаза» по закону Бертло — Нернста оспаривалась рядом видных ученых, в том числе Г. Тамманом и О. Ханом. Основным теоретическим дово­дом этих ученых являлось то, что в силу чрезвычайной медлен­ности диффузионных процессов в твердом теле при низких тем­пературах они не могут обеспечить состояния истинного термо­динамического равновесия между кристаллами и раствором.

Но исследования В. Г. Хлопина и его учеников показали, что в определенных условиях в таких системах может устанав­ливаться истинное термодинамическое равновесие, и, следова­тельно, должен иметь место закон распределения Бертло — Нернста. Отправным моментом для этих исследований послу­жили наблюдения за разделением радия и бария в процессе дробной кристаллизации их хлоридов. Наблюдения эти гово­рили о том, что исследователи имели дело с системами, весьма близкими к состоянию истинного равновесия между кристал­лами и раствором. Поэтому распределение радия при процессах дробной кристаллизации можно было рассматривать как рас­пределение вещества между двумя несмешивающимися раство­рителями (в данном случае между кристаллической фазой и раствором). Следовало ожидать далее, что распределение это будет подчиняться закону Бертло — Нернста, что и оправдалось в действительности.

Одной из важнейших причин успеха исследований В. Г. Хло­пина и его учеников явилось применение в качестве распреде­ляющихся веществ радиоактивных элементов, т. е. изучение си­стем, крайне разбавленных в отношении одного из компонентов, что обеспечивало выполнение второго условия, необходимого для достижения распределения компонентов по закону Бертло — Нернста.

В своих первых работах по изучению соосаждения солей ба­рия и радия В. Г. Хлопин и его ученики использовали для вы­числения константы K_N соотношение :

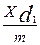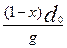: = K_N (2)

где g — масса жидкой фазы;

т — масса твердой кристаллической фазы;

d ₀ и d₁ — плотности твердой и жидкой фаз;

х — доля микрокомпонента, перешедшая в твердую фазу;

1-х — доля микрокомпонента, оставшаяся в жидкой фазе

В дальнейшем для представления экспериментальных данных по распределению компонентов между сосуществующими фазами более удобной оказалась формула, предложенная Л. Гендерсоном и Ф. Крэчеком:

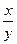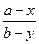: =D (3)

где х и у - количества макро- и микрокомпонентов, перешедших в кристаллическую фазу; а и b — первоначальные количества макро- и микрокомпонентов в системе; D — коэффициент кристаллизации.

Величина D отражает сущность процесса распределения микрокомпонента между кристаллической фазой и раствором: она показывает, во сколько раз отношение между количествами микро- и макрокомпонентов в кристаллах больше (D > 1), равно (D = 1) или меньше (D < 1), чем аналогичное отношение в растворе, равновесном с кристаллами.

Было показано, что связь между константами распределения (K_N) и кристаллизации (D) дается выражением:

D = K_N∙ 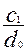(4)

Где с₁- концентрация микрокомпонента в равновесном растворе; d₀ – плотность кристаллической фазы.

Экспериментальное доказательство применимости закона Бертло — Нернста к распределению электролитов между раство­рами и кристаллами оказалось довольно трудным. Это объясня­лось, в основном, тем, что благодаря практически полному от­сутствию в кристаллах диффузии (при комнатной температуре) не удавалось осуществить первое из отмеченных выше усло­вий — истинное равновесие между раствором и кристаллами. Однако и при низких температурах удалось в конце концов найти путь, ведущий к выравниванию концентраций в твердой фазе. Таким путем, как показал В. Г. Хлопин, может служить перекристаллизация.

Оказалось, что в случае образования кристаллов из сильно пересыщенных растворов число первоначально возникающих кристаллизационных центров во много раз превышает число выросших впоследствии кристаллов. Таким образом, росту кри­сталлов предшествует образование большого числа зародышей, которые еще в стадии субмикронов успевают многократно пере­кристаллизоваться и таким путем гомогенизироваться. Рост кристаллов в этом случае происходит путем срастания отдель­ных однородных кристаллов (субмикронов),

Для подтверждения возможности экспериментального осуществления истинного термодинамического равновесия между твердой кристаллической фазой и раствором В. Г. Хлопин использовал несколько путей.

Первый путь состоял в длительной многократной перекри­сталлизации кристаллов макрокомпонента в его насыщенном растворе, содержащем микрокомпонент. С этой целью в стек­лянные пробирки отвешивали примерно равные количества мелкоизмельченной соли чистого макрокомпонента, а затем до­бавляли в них по 25 мл насыщенного раствора макрокомпо­нента, содержащего радиоактивный элемент. После этого про­бирки помещали в термостат и энергично перемешивали смесь до тех пор, пока концентрация микрокомпонента в насыщенном растворе не переставала изменяться. После окончания опыта отбирали пробы раствора для определения содержания в них макро- и микрокомпонента. Как показали опыты, время уста­новления равновесия зависит от свойств макрокомпонента и температуры (при 25° оно составляет примерно 3—4 недели).

Этот путь позволял проследить за ходом установления равновесия «снизу».

Второй путь состоял в кристаллизации из пересыщенного раствора при энергичном перемешивании. С этой целью приго­товляли насыщенный при определенной температуре (обычно О и 25°) раствор макрокомпонента, содержащий микрокомпо­нент, и мелкоизмельченную чистую соль макрокомпонента. В стеклянные пробирки емкостью 75—100 мл, снабженные при­тертыми пробками, отвешивали различные количества соли макрокомпонента и добавляли по 25 мл насыщенного раствора. Количество добавленного раствора определяли взвешиванием. После этого пробирки закрывали и нагревали на водяной бане до полного растворения твердой фазы. По окончании растворе­ния пробирки помещали в термостат, имеющий температуру, одинаковую с той, при которой приготовлялся насыщенный раствор макрокомпонента. После этого раствор энергично пере­мешивали в течение 4—8 часов до полного снятия пересыщения. Далее отделяли осадок и производили химический анализ твер­дой и жидкой фаз на содержание в них макро- и микрокомпо­нента

Третий путь состоял в длительной многократной перекри­сталлизации заранее приготовленных смешанных кристаллов макро- и микрокомпонента в насыщенном растворе макроком­понента. С этой целью приготовляли насыщенный при опреде­ленной температуре раствор чистого макрокомпонента и мелко­измельченные смешанные кристаллы макро- и микрокомпонента. Далее отвешивали приблизительно равные количества смешан­ных кристаллов, добавляли 25 мл насыщенного раствора и про­изводили длительное перемешивание при определенной темпе­ратуре до установления равновесия. После этого раствор и твердую фазу анализировали на содержание в них макро- и микрокомпонента.

Этот путь позволял проследить за ходом установления равновесия «сверху».

Таким образом, при условии достижения истинного термоди­намического равновесия распределение изоморфного или изодиморфного микрокомпонента должно подчиняться соотношению (1), т. е. следовать закону, который применительно к системе типа жидкость — твердое тело называется законом Хлопина и может быть сформулирован в общей форме следующим обра­зом: при достижении термодинамического равновесия между кристаллами и раствором двух веществ, способных образовы­вать истинные твердые растворы, распределение компонентов между фазами следует линейному закону, согласно которому отношение концентраций компонентов в сосуществующих фазах является величиной, не зависящей от соотношения объе­мов фаз.

При ничтожно малых концентрациях одного из компонен­тов К_N не только не зависит от соотношения объемов фаз, но и сохраняет свое значение в весьма широком интервале концен­траций (обычно до 10^{-2 М).} При значительном увеличении кон­центраций К_N, как правило, изменяется, поскольку изменяется состав фаз.

Если вместо концентраций использовать активности, то ве­личина К_N оказывается постоянной при любых концентрациях компонента.