Теорема о почленном интегрировании.

Пусть 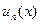непрерывны в V, пусть ряд 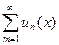равномерно сходится в V. Тогда ряд 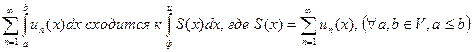, то есть функциональный ряд можно почленно интегрировать.

Заметим, что суть теоремы содержится в формуле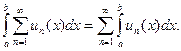

Доказательство. Так как ряд 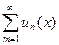равномерно сходится в V, то его сумма S(x) непрерывна (теорема о непрерывности суммы ряда) и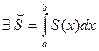

Так как 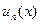непрерывны, то 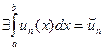. Составим ряд 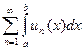, покажем, что он сходится к 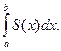Обозначим частичную сумму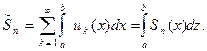

Так как ряд 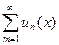равномерно сходится в V, то .

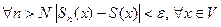Оценим .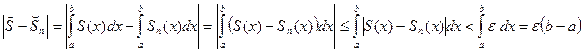

Теорема о почленном дифференцировании.

Пусть 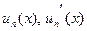непрерывны в V. Пусть ряд 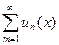сходится в V, а ряд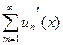

.равномерно сходится в V. Тогда ряд 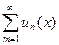можно почленно дифференцировать, причем ( = .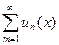

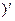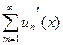Доказательство. Так как ряд 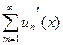сходится равномерно, то его сумма 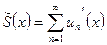- непрерывная функция (теорема о непрерывности суммы ряда). Ее можно интегрировать, применяя теорему о почленном интегрировании.

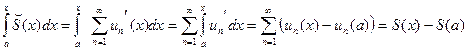
Дифференцируя, получим 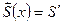, то есть .

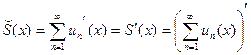Лекция 14. Степенные ряды.

Степенным рядомназывается ряд вида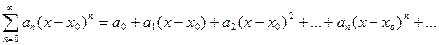

Степенной ряд заведомо сходится при 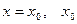- центр сходимости ряда.

Теорема Абеля.

1) Пусть степенной ряд сходится в точке 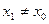. Тогда он абсолютно сходится в интервале

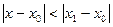, симметричном относительно .

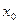2) Пусть степенной ряд расходится в точке 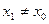. Тогда он расходится в области .

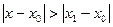Доказательство.

1) Пусть степенной ряд сходится в точке 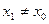, тогда числовой ряд 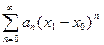сходится. Тогда по необходимому признаку сходимости ряда 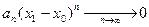. Тогда .

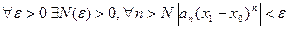Рассмотрим произвольное, но фиксированное .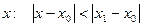

Оценим ,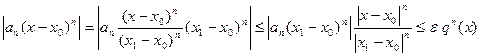

где .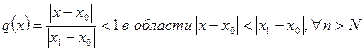

По первому признаку сравнения числовых знакоположительных рядов ряд 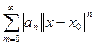сходится в указанной области (сравнение с бесконечно убывающей геометрической прогрессией 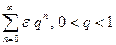. Следовательно, в области 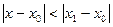степенной ряд абсолютно сходится.

2) Пусть степенной ряд расходится в точке 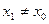. Рассмотрим 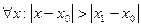. Если бы ряд сходился в точке x, то он по п. 1 доказательства сходился бы в точке 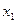. Противоречие.

Замечание. Для каждой точки x константа q(x) своя. Может не найтись константы, меньшей единицы и ограничивающей сверху константы q(x) для всех точек области V.

Поэтому абсолютная сходимость есть, но равномерной сходимости степенного ряда в области V не гарантируется.

Если такая константа найдется, то гарантируется равномерная сходимость ряда.