Определение радиуса и интервала сходимости степенного ряда.

Зафиксируем некоторое значение x и запишем ряд из модулей членов степенного ряда

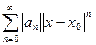. Это – знакоположительный числовой ряд. Применим к нему признак Даламбера или радикальный признак Коши.

Применяя признак Даламбера, имеем

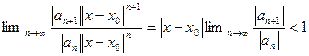. Отсюда .

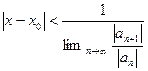Поэтому .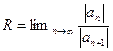

Применяя радикальный признак Коши, имеем

.

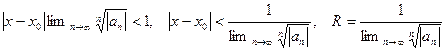Так определяется радиус сходимости степенного ряда.

Затем исследуется сходимость ряда на границе интервала сходимости, в точках 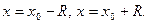Эти точки подставляются в исходный ряд, ряд становится обычным числовым рядом и исследуется стандартными методами для числовых рядов.

Пример. .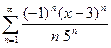

Составим ряд из модулей 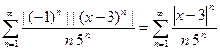, применим радикальный признак Коши .

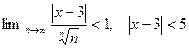Радиус сходимости R=5, интервал сходимости (-2, 8). Исследуем сходимость ряда на границе, подставляя точки x= -2, в исходный ряд..

В точке x = -2 имеем ряд 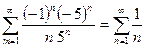- гармонический ряд, он расходится.

В точке x = 8 имеем ряд 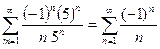- сходящийся (по признаку Лейбница) знакочередующийся ряд.

Область сходимости исходного ряда (-2, 8].

Теорема.Степенной ряд равномерно сходится внутри интервала сходимости.

Доказательство. Пусть 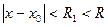. Выберем 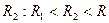, например 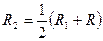. На интервале 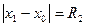и в точке x₁ степенной ряд сходится абсолютно, так как этот интервал лежит внутри интервала сходимости. Тогда (точно так же, как в доказательстве теоремы Абеля оценим ,

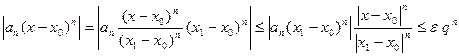где 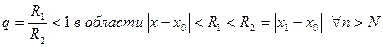( 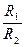не зависит от ).

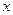Тогда в области 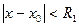степенной ряд будет сходиться равномерно по признаку Вейерштрасса (члены ряда мажорируются членами бесконечно убывающей геометрической прогрессии).

Следствие.Внутри интервала сходимости справедливы теоремы о непрерывности суммы ряда, о почленном интегрировании и дифференцировании ряда.

Теорема.При почленном дифференцировании и интегрировании степенного ряда его радиус сходимости не меняется.

Доказательство. Рассмотрим ряд из модулей членов степенного ряда (это – знакоположительный числовой ряд в конкретной точке) и определим радиус сходимости по признаку Даламбера.

.

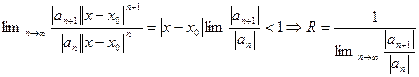Продифференцируем почленно степенной ряд 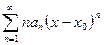, перейдем к ряду из модулей и найдем радиус сходимости по признаку Даламбера.

.

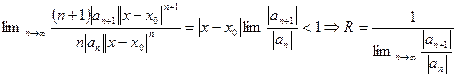Таким образом, при почленном дифференцировании радиус сходимости степенного ряда не меняется. Он не меняется и при почленном интегрировании, иначе он изменился бы при почленном дифференцировании.