Знакочередующиеся ряды.
Знакопеременный ряд называется знакочередующимся, если знаки членов ряда чередуются, т.е. ряд 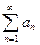 имеет вид
имеет вид 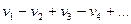 . Предполагаем, что ряд начинается с положительного члена,
. Предполагаем, что ряд начинается с положительного члена, 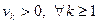 .
.
К знакочередующимся рядам можно применить все теоремы, доказанные выше для знакопеременных рядов. Но есть специальный, очень удобный достаточный признак сходимости знакочередующихся рядов – признак Лейбница (он не является необходимым признаком).
Признак Лейбница.
Пусть
1. ряд 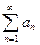 имеет вид
имеет вид 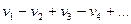 (знакочередующийся,
(знакочередующийся, 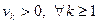 )
)
2. последовательность 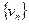 монотонно убывает
монотонно убывает
3. 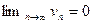
Тогда 1) ряд 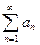 сходится
сходится
2) 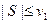
Доказательство. Рассмотрим последовательность частичных сумм с четными номерами
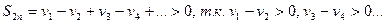 (последовательность
(последовательность 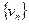 монотонно убывает по условию теоремы).
монотонно убывает по условию теоремы).
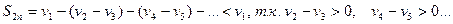
Т.е. последовательность 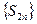 ограничена сверху
ограничена сверху 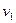 .
.
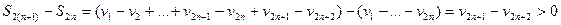
Т.е. последовательность 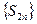 монотонно возрастает.
монотонно возрастает.
По теореме Вейерштрасса существует 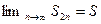 .
.
Рассмотрим теперь последовательность частичных сумм с нечетными номерами
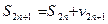 .
.
По условию 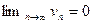 , т.е.
, т.е. 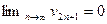 .
.
По доказанному выше 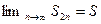 . Следовательно, предел правой части равенства существует и равен
. Следовательно, предел правой части равенства существует и равен 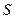 . Поэтому предел левой части равенства тоже существует и равен
. Поэтому предел левой части равенства тоже существует и равен
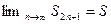 .
.
Раскроем определение предела 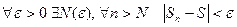 как для четных n, так и для нечетных n. Следовательно, это справедливо для любых
как для четных n, так и для нечетных n. Следовательно, это справедливо для любых 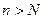 , поэтому
, поэтому 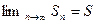 .
.
Из доказанного выше неравенства 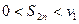 . Переходя к пределу, получим
. Переходя к пределу, получим 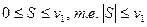 .
.
Следствие. 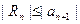 .Остаток ряда оценивается модулем первого отброшенного члена ряда.
.Остаток ряда оценивается модулем первого отброшенного члена ряда.
Доказательство. Так как остаток знакочередующегося ряда тоже знакочередующийся ряд, то его сумма по признаку Лейбница оценивается модулем его первого члена.
То есть 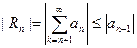 . А первый член остатка ряда и есть первый отброшенный член.
. А первый член остатка ряда и есть первый отброшенный член.
Пример. Ряд 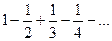
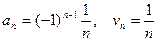 . Ряд сходится по признаку Лейбница. Ряд из модулей – расходящийся гармонический ряд. Следовательно, ряд сходится условно.
. Ряд сходится по признаку Лейбница. Ряд из модулей – расходящийся гармонический ряд. Следовательно, ряд сходится условно.
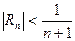
Дата добавления: 2017-11-21; просмотров: 1063;











