Применение степенных рядов.

1. Вычисление значений функций

Пример. Вычислить arctg 0.3 с точностью .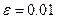

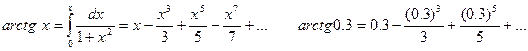
По следствию из признака Лейбница остаток числового знакочередующегося ряда оценивается модулем первого отброшенного члена.

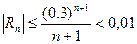. Из этого неравенства найдем n, n=2. .

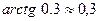Если разложение – знакопостоянный ряд, то надо подобрать какой-либо мажорантный ряд с известной суммой, например, оценить сверху члены ряда членами бесконечно убывающей геометрической прогрессии и оценку суммы ряда проводить по сумме прогрессии.

2. Вычисление интегралов.

Пример. Вычислить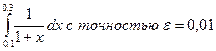

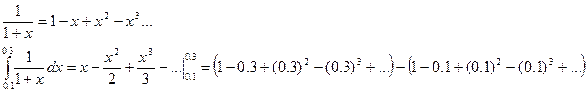
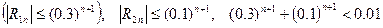
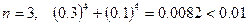
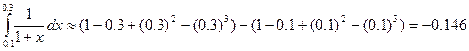
3. Решение дифференциальных уравнений.

Пример.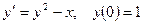

1 способ. Представим 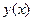в виде степенного ряда с неопределенными коэффициентами до 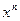(n – заранее определено). Это разложение подставляется в левую и правую часть, и приравниваются коэффициенты при равных степенях x. Решается система алгебраических уравнений и определяются коэффициенты.

.

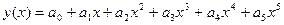Заметим, что при дифференцировании степень понижается на единицу, поэтому в разложении нужно запасать членов на k больше n, где k – порядок дифференциального уравнения.

Разложение проводится по степеням (x - x₀₎, если начальные условия заданы в точке x₀.

В данном уравнении производится разложение в ряд Маклорена, так как начальное условие задано в нуле.

.

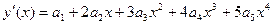Подставляем разложения в правую и левую части уравнения .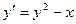

= . .

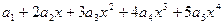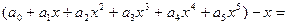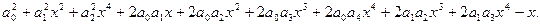
Удерживаем в разложении члены четвертых степеней, в коэффициентах при x⁵ будут

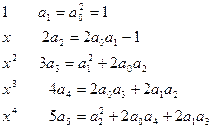
Отсюда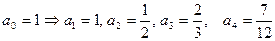

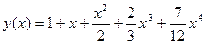
2 способ. Представим 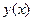в виде ряда Тейлора.

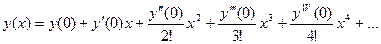
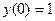
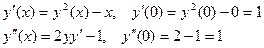
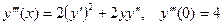
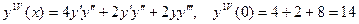
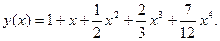
[1] Здесь рассматривается упрощенный вариант построения интеграла, более общий вариант рассмотрен в седьмом выпуске учебника «Математика в техническом университете» под ред. проф. В.С. Зарубина и проф. А.П. Крищенко М. Изд. МГТУ им. Н.Э. Баумана 2001 (далее просто учебник).

[2] Здесь рассматривается непрерывная функция, более общий вариант см. в седьмом томе учебника

[3] Далее граница области предполагается кусочно-гладкой

[4] Это замечание относится ко всем рассматриваемым далее интегралам

[5] При обсуждении свойств предполагается выполнение условий теоремы существования

[6] предполагается, что в области есть только одна точка разрыва функции

[7] Здесь интеграл вводится несколько упрощенно. Более строгое определение интеграла приведено в выпуске VII учебника.

[8] Эти требования можно ослабить, распространив интеграл на функции со счетным числом разрывов первого рода (выпуск VII.учебника).

[9] Это очевидно, иначе предел не существует, но это стоит подчеркнуть.

[10] Здесь рассматривается непрерывная функция, более общий вариант см. в седьмом томе учебника

[11] Это требование может быть ослаблено, более общий вариант см. в седьмом томе учебника

[12] Это требование может быть ослаблено, более общий вариант см. в седьмом томе учебника