Лекция 15. Ряд Тейлора.

Ряд Тейлора.

Рядом Тейлора называется степенной ряд вида 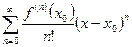(предполагается, что функция 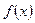является бесконечно дифференцируемой).

Рядом Маклоренаназывается ряд Тейлора при 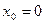, то есть ряд .

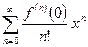Теорема.Степенной ряд является рядом Тейлора для своей суммы.

Доказательство. Пусть 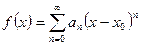и степенной ряд сходится в интервале 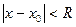. Подставим в разложение 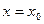, получим .

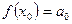Так как степенной ряд сходится равномерно внутри интервала сходимости, мы можем его дифференцировать почленно. Полученный ряд будет сходиться в том же интервале, так как радиус сходимости при дифференцировании не меняется. Его вновь можно дифференцировать почленно и т.д. Вычислим коэффициенты в степенных рядах, полученных почленным дифференцированием. = ,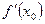

, , ,

, , ,

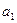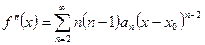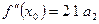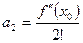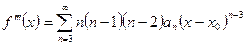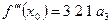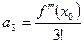Продолжая этот процесс, получим 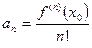. Это – коэффициенты ряда Тейлора. Поэтому степенной ряд есть ряд Тейлора.

Следствие.Разложение функции в степенной ряд единственно.

Доказательство. По предыдущей теореме коэффициенты разложения функции в степенной ряд определяются однозначно, поэтому разложение функции в степенной ряд единственно.