Разложение в ряд Маклорена основных элементарных функций.
Запишем разложения в ряд Маклорена основных элементарных функций, вычисляя коэффициенты разложения по формуле 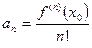 , где
, где 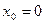 .
.
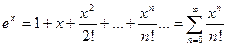

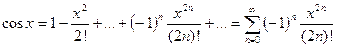
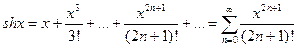
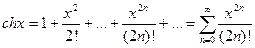
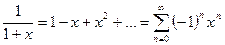 ,
, 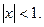
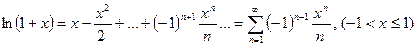 (интегрируя предыдущую формулу)
(интегрируя предыдущую формулу)
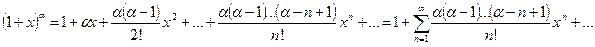
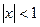 ,
, 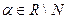 .
.
Пусть записано разложение функции в степенной ряд. Возникает вопрос, всегда ли это разложение (степенной ряд) сходится именно к этой функции, а не к какой-либо другой.
Теорема.Для того чтобы ряд Тейлора сходился к той функции, по которой он построен, необходимо и достаточно, чтобы остаточный член формулы Тейлора стремился к нулю при 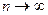 .
.
Доказательство. Запишем формулу Тейлора, известную из 1 семестра
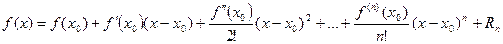
Необходимость. Обозначим Sn – частичную сумму ряда Тейлора .
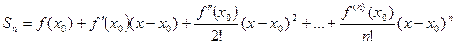 .
.
Если ряд Тейлора сходится к 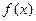 , то
, то 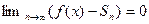 . Но по формуле Тейлора
. Но по формуле Тейлора 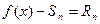 . Следовательно,
. Следовательно, 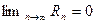 .
.
Достаточность. Если 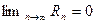 , то
, то 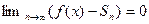 , а
, а 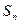 - частичная сумма ряда Тейлора. Поэтому ряд Тейлора сходится именно к функции
- частичная сумма ряда Тейлора. Поэтому ряд Тейлора сходится именно к функции 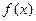 .
.
Теорема.Пусть все производные функции 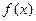 ограничены в совокупности одной константой.
ограничены в совокупности одной константой. 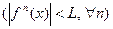 Тогда ряд Тейлора сходится к функции
Тогда ряд Тейлора сходится к функции 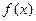 .
.
Доказательство. Оценим остаточный член формулы Тейлора
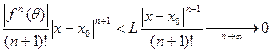 , так как показательная функция растет медленнее, чем n!. Поэтому (по предыдущей теореме) ряд Тейлора сходится к функции
, так как показательная функция растет медленнее, чем n!. Поэтому (по предыдущей теореме) ряд Тейлора сходится к функции 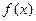 .
.
В качестве примера применения теоремы рассмотрим разложение в ряд Маклорена функций sin x, cos x. Эти ряды сходятся к функциям, так как их производные ограничены в совокупности единицей на всей оси.
В разложении функции ex на отрезке [a, b] все производные функции ограничены константой eb, поэтому ряд для функции ex сходится к ней на любом конечном отрезке.
Ряды для функций sh x, ch x можно получить линейной комбинацией экспонент, следовательно, ряды для этих функций сходятся к ним на всей оси.
Рассмотрим разложение в ряд функции 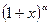 . Предположим, что ряд сходится к функции
. Предположим, что ряд сходится к функции 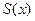 . Можно, дифференцируя ряд почленно, установить справедливость соотношения
. Можно, дифференцируя ряд почленно, установить справедливость соотношения 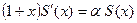 (выведите его в качестве упражнения). Решая это дифференциальное уравнение, получим
(выведите его в качестве упражнения). Решая это дифференциальное уравнение, получим 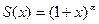 .
.
Дата добавления: 2017-11-21; просмотров: 1794;











