Формула Остроградского – Гаусса.
Пусть компоненты векторного поля 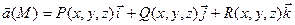 непрерывны и имеют непрерывные частные производные в пространственно односвязной замкнутой области V и на ее кусочно гладкой границе
непрерывны и имеют непрерывные частные производные в пространственно односвязной замкнутой области V и на ее кусочно гладкой границе 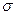 .
.
Тогда справедлива формула Остроградского – Гаусса
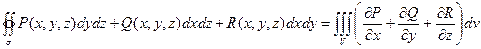 .
.
Заметим, что левая часть формулы представляет собой поток векторного поля 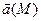 через поверхность
через поверхность 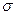 .
.
Доказательство. 1) Формула Остроградского – Гаусса, в силу произвольности P, Q, R состоит из трех частей, в каждую из которых входит одна из компонент векторного поля P, Q, R. В самом деле, можно взять P = 0, Q = 0 и доказывать отдельно часть формулы в которую входит только R. Остальные части формулы (при P = 0, R = 0, Q = 0, R = 0) доказываются аналогично. Будем доказывать часть формулы
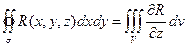
2) Для доказательства выбранной части формулы представим пространственную область V в виде объединения конечного числа цилиндрических тел, не имеющих общих внутренних точек, с образующими, параллельными оси OZ. Доказательство можно проводить для цилиндрического тела. В самом деле, тройной интеграл в правой части равен сумме тройных интегралов по цилиндрическим телам (свойство аддитивности). Поверхностный интеграл в левой части также равен сумме поверхностных интегралов по полным поверхностям цилиндрических тел, причем при суммировании интегралы по общим границам соседних цилиндрических тел будут сокращаться из-за противоположного направления внешних нормалей на общих границах.
Итак, будем доказывать соотношение 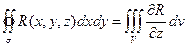 для цилиндрического тела V, проектирующегося в область D на плоскости OXY. Пусть «верхняя» граница цилиндрического тела – поверхность
для цилиндрического тела V, проектирующегося в область D на плоскости OXY. Пусть «верхняя» граница цилиндрического тела – поверхность 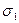 описывается уравнением
описывается уравнением 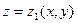 , «нижняя» граница – поверхность
, «нижняя» граница – поверхность 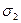 описывается уравнением
описывается уравнением 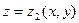 . Боковую поверхность цилиндрического тела, параллельную оси OZ, обозначим
. Боковую поверхность цилиндрического тела, параллельную оси OZ, обозначим 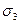 .
.
Сразу заметим, что поток векторного поля через боковую поверхность равен нулю. Действительно, 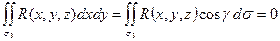 , так как нормаль на боковой поверхности ортогональна оси OZ и
, так как нормаль на боковой поверхности ортогональна оси OZ и 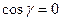 .
.
Заметим также, что на «верхней» поверхности 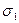
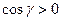 , а на «нижней поверхности
, а на «нижней поверхности 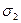
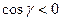 . Поэтому при переходе от поверхностного интеграла по
. Поэтому при переходе от поверхностного интеграла по 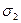 к двойному интегралу по области D и обратно надо менять знак, а при переходе от поверхностного интеграла по
к двойному интегралу по области D и обратно надо менять знак, а при переходе от поверхностного интеграла по 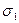 к двойному интегралу по области D и обратно менять знак не надо .
к двойному интегралу по области D и обратно менять знак не надо .

  
| 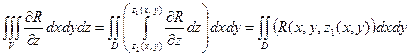 - -
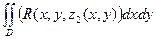 = = 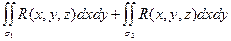 = =
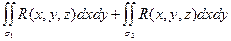 + + 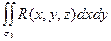 = =
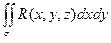 Таким образом, соотношение
Таким образом, соотношение 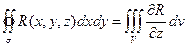 доказано. доказано.
|
Замечание. Формулу Остроградского – Гаусса можно записать в «полевом» виде
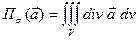 - поток векторного поля через замкнутую поверхность
- поток векторного поля через замкнутую поверхность 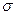 равен объемному интегралу от дивергенции поля по области, ограниченной поверхностью
равен объемному интегралу от дивергенции поля по области, ограниченной поверхностью 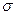 .
.
Дивергенция векторного поля(расходимость) есть 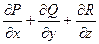 .
.
Дивергенция – это характеристика векторного поля, инвариантная относительно системы координат. Покажем это.
Инвариантное определение дивергенции.
Рассмотрим произвольную точку M в пространственной области V. Выберем ее окрестность VM – шар радиуса r с центром в точке M. Обозначим 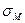 - ее границу – сферу радиуса r. По теореме о среднем для тройного интеграла
- ее границу – сферу радиуса r. По теореме о среднем для тройного интеграла
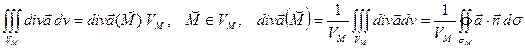 (по формуле Остроградского – Гаусса).
(по формуле Остроградского – Гаусса).
Стягиваем окрестность к точке M, получаем дивергенцию векторного поля в точке M.
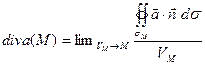 . Это и есть инвариантное определение дивергенции.
. Это и есть инвариантное определение дивергенции.
Поэтому дивергенция векторного поля в точке M имеет смысл объемной плотности потока векторного поля через окрестность этой точки и характеризует мощность источника (если 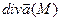 >0) или стока (если
>0) или стока (если 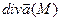 <0) векторного поля в точке M.
<0) векторного поля в точке M.
Если 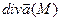 >0, то точка M – источник векторного поля, если
>0, то точка M – источник векторного поля, если 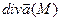 <0, то точка M – сток векторного поля. Если в некоторой области дивергенция равна нулю, то в этой области нет ни источников, ни стоков, поток векторного поля через границу такой области равен нулю – «сколько поля втекает в область, столько и вытекает из нее».
<0, то точка M – сток векторного поля. Если в некоторой области дивергенция равна нулю, то в этой области нет ни источников, ни стоков, поток векторного поля через границу такой области равен нулю – «сколько поля втекает в область, столько и вытекает из нее».
Пример. Определить расположение источников и стоков векторного поля 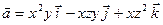 . Выяснить, является ли точка M(1,2,3) источником или стоком.
. Выяснить, является ли точка M(1,2,3) источником или стоком.
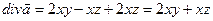 . Все точки, для которых 2xy+xz >0 – источники, все точки, для которых 2xy+xz <0 – стоки. На поверхности 2xy+xz = 0 нет ни источников, ни стоков. Точка M – источник, так как
. Все точки, для которых 2xy+xz >0 – источники, все точки, для которых 2xy+xz <0 – стоки. На поверхности 2xy+xz = 0 нет ни источников, ни стоков. Точка M – источник, так как 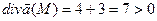 .
.
Дата добавления: 2017-11-21; просмотров: 1845;











