Задача о потоке жидкости через поверхность.
Поток жидкости через поверхность 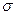 .– это количество жидкости, протекающее через поверхность
.– это количество жидкости, протекающее через поверхность 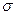 в единицу времени.
в единицу времени.
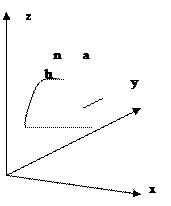      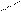   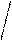  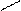 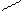 
| Пусть на элементе поверхности 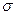 площадке площадке 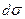 в некоторой ее точке M проведен вектор в некоторой ее точке M проведен вектор 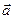 перемещения частицы жидкости через площадку перемещения частицы жидкости через площадку 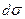 в единицу времени. Предполагаем, что для всех точек в единицу времени. Предполагаем, что для всех точек 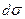 перемещение одинаково по величине и направлению. Поток жидкости можно вычислить как объем наклонного (по направлению вектора перемещений) параллелепипеда, построенного на перемещение одинаково по величине и направлению. Поток жидкости можно вычислить как объем наклонного (по направлению вектора перемещений) параллелепипеда, построенного на 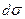 . Этот объем равен . Этот объем равен 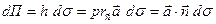 , где , где 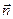 - единичный вектор нормали к поверхности. Тогда поток жидкости равен П = - единичный вектор нормали к поверхности. Тогда поток жидкости равен П = 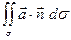
|
Здесь мы вычисляли дифференциал потока, а затем интегрировали по всей поверхности – это метод дифференциалов при построении интеграла.
Можно строить интеграл с помощью метода интегральных сумм, как мы действовали обычно.
- Введем разбиение области на элементы так, чтобы соседние элементы не содержали общих внутренних точек (условие А),
- на элементах разбиения отметим точку М. Предполагая перемещение частиц жидкости постоянным на элементе и равным 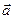 (M), вычислим приближенно поток через элемент разбиения и просуммируем его по элементам, получая интегральную сумму
(M), вычислим приближенно поток через элемент разбиения и просуммируем его по элементам, получая интегральную сумму 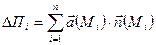 .
.
- Измельчим разбиение при условии 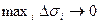 (условие В) и перейдем к пределу получая поверхностный интеграл второго рода
(условие В) и перейдем к пределу получая поверхностный интеграл второго рода
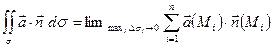 .
.
По виду это – поверхностный интеграл первого рода, он и имеет те же свойства, что поверхностный интеграл первого рода, но имеет еще и свойство ориентируемости. Интеграл по внешней стороне поверхности отличается знаком от интеграла по внутренней стороне поверхности, так как на различных сторонах поверхности нормали в той же точке нормали направлены по одной прямой в различные стороны.
Теорема существования формулируется так же, как для поверхностного интеграла первого рода с тем же замечанием о независимости интеграла от способа выбора разбиения (лишь бы выполнялись условия А), от выбора точек на элементах разбиения, от способа измельчения разбиения (лишь бы выполнялось условие В).
Дата добавления: 2017-11-21; просмотров: 1790;











