Скалярное и векторное поля.

Говорят, что в области (плоской или пространственной) задано скалярное полеj (M), если в этой области задана скалярная функция j (M).

Говорят, что в области (плоской или пространственной) задано векторное поле 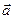(M), если в этой области задана векторная функция 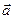(M).

Например, масса или температура частиц в комнате – скалярные поля, скорость или силы взаимодействия частиц – векторные поля.

В интегралах первого рода :двойных, криволинейных, поверхностных мы имели дело со скалярным полем – распределением масс точек кривой или поверхности в пространстве.

В интегралах второго рода вычислялись характеристики векторных полей: работа векторного поля (силового поля) в криволинейном интеграле, поток векторного поля в поверхностном интеграле.

Рассмотрим подробнее основные характеристики скалярных и векторных полей.

Скалярные поля.

Линии уровня плоского поля j (x, y) – кривые, на которых значения функции постоянны j (x, y) = С.

Например, линии равной высоты, нанесенные на географической карты (h (x, y) = 0 – уровень моря, h = 7000м – немногие горные вершины, h = - 10000м – самые глубокие океанские впадины).

Поверхности уровня пространственного поля j (x, y, z) – поверхности, на которых значения функции постоянны j (x, y, z) = С.

Например, поверхности равной температуры или давления в атмосфере. Любая линия на поверхности уровня – это линия уровня.

Пример. Задано поле 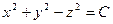. При С > 0 поверхности уровня – однополостные гиперболоиды, при С = 0 поверхность уровня – конус, при С < 0 поверхности уровня – двуполостные гиперболоиды.

Линии или поверхности различных уровней не пересекаются.

Чем чаще (гуще) поверхности или линии уровня, тем интенсивнее изменение поля.

Градиент поля – вектор .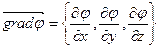

Утверждение. Градиент скалярного поля ортогонален его поверхности уровня.

Доказательство. Пусть точка (x, y, z) остается на поверхности уровня g(x, y, z) = 0 при вариациях переменных. Тогда равенство превращается в тождество, а тождество можно дифференцировать.

.

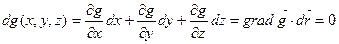Вектор 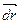(x, y, z) - это вектор, касательный в точке (x, y, z) к любой кривой, лежащей на поверхности уровня, проходящей через эту точку. Поэтому в точке (x, y, z) вектор градиента ортогонален всем касательным к линии уровня, проходящим через эту точку. Следовательно, он ортогонален касательной плоскости к поверхности уровня и направлен по нормали к поверхности уровня.

Производная скалярного поля по направлению 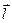определяется как 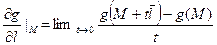. Известно из теории функций многих переменных (выпуск V учебника), что производная по направлению есть проекция градиента на данное направление

.

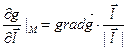Пример. Найти производную скалярного поля g(x, y, z) = x² + y² + z³ по направлению {1,3,2} в точке (1,0,4)

.

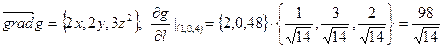Векторное поле.

Векторная линия -линия, в каждой точке которой вектор поля направлен по касательной к ней.

Уравнения векторной линии легко получить из условия коллинеарности векторов поля 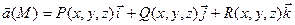и касательной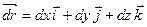

.

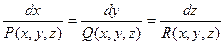Пример. Написать уравнения векторных линий векторного поля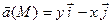

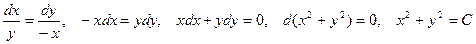- линии уровня – окружности (С>0).

Векторной трубкойназывается поверхность, образованная векторными линиями.