Запись поверхностного интеграла второго рода.
Запишем вектор перемещений частиц и нормаль в точке M(x, y, z), выделяя скалярные компоненты векторов
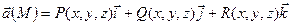 ,
, 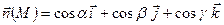
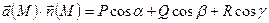
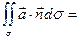
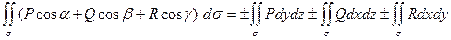
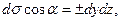
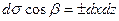 ,
, 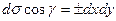 . Знак «+» выбирается, если угол между нормалью к поверхности и осью (OX в первом интеграле, OY во втором, OZ в третьем) острый, знак «-» выбирается, если угол тупой. В самом деле, в поверхностных интегралах площади элементов поверхности положительны, а знаки «+» или «–» компенсируют знак косинуса угла между нормалью и координатной осью. При переходе от поверхностных интегралов к двойным одна из координат подставляется из уравнения поверхности, чтобы точка (x, y, z) находилась на поверхности
. Знак «+» выбирается, если угол между нормалью к поверхности и осью (OX в первом интеграле, OY во втором, OZ в третьем) острый, знак «-» выбирается, если угол тупой. В самом деле, в поверхностных интегралах площади элементов поверхности положительны, а знаки «+» или «–» компенсируют знак косинуса угла между нормалью и координатной осью. При переходе от поверхностных интегралов к двойным одна из координат подставляется из уравнения поверхности, чтобы точка (x, y, z) находилась на поверхности 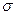 .
.
Пример. Найти поток радиуса-вектора через полную поверхность тетраэдра, ограниченного координатными плоскостями и плоскостью x + y + z = 1
| Поток радиус-вектора через координатные плоскости нулевой, так как на них радиус-вектор точки лежит в координатной плоскости и ортогонален нормали к координатной плоскости, т.е. 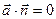 .
Вычислим поток через грань тетраэдра, лежащую в плоскости x + y + z =1. Он и будет суммарным потоком, так как поток через остальные грани нулевой. Для этой грани .
Вычислим поток через грань тетраэдра, лежащую в плоскости x + y + z =1. Он и будет суммарным потоком, так как поток через остальные грани нулевой. Для этой грани 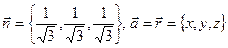 , площадь грани – треугольника по теореме Пифагора равна , площадь грани – треугольника по теореме Пифагора равна 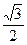 (проверьте).
Поток равен (проверьте).
Поток равен 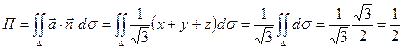
|
Поток равен 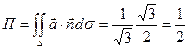 .
.
Вычислим поток через двойные интегралы проектированием на координатные плоскости. Поток радиус-вектора через координатные плоскости нулевой. Тогда
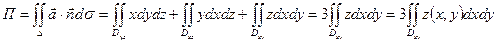 =
=
= 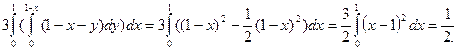 .
.
Получили тот же результат.
Лекция 8
Дата добавления: 2017-11-21; просмотров: 1267;











