ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ КОЛЕБАНИЙ

Линейные дифференциальные уравнения второго порядка широко используют при изучении явлений, связанных с разнообразными колебаниями.

Пусть в некоторой среде вдоль оси Ох движется материальная точка массы m. Предположим, что на эту точку действуют следующие силы: сила f ₁ = –ax (a > 0 – коэффициент обновления), которая пытается вернуть точку в начало координат; сила сопротивления среды

f ₂ = –bx´ (b > 0 – коэффициент сопротивления); внешняя сила f ₃ = f (t), направление которой совпадает с направлением оси Ох.

Задача состоит в том, чтобы найти закон x = x(t), по которому движется точка. Воспользовавшись вторым законом Ньютона, запишем дифференциальное уравнение движения

mx´´= –bx´ – ax + f (t)

или x´´ + 2hx´ + ω²x = φ(t), (1)

где 2h = 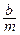, ω² = 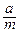, φ(t) = .

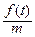Если φ(t) 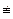0, то дифференциальное уравнение (1) называют уравнением вынужденных колебаний, а при φ(t) ≡ 0 – уравнением свободных колебаний.

Отметим, что уравнения вида (1) описывают механические колебания груза на пружинной рессоре (колебания железнодорожных вагонов, автомобилей и т. д.), малые колебания математического или физического маятника, вертикальные и бортовые колебания корабля, электрические, звуковые и много других колебаний.