Структура общего решения линейного однородного дифференциального уравнения

Т.о., для того, чтобы получить общее решение однородного уравнения (2), достаточно найти любые два линейно независимых частных решения этого уравнения (в этом случае говорят, что они образуют фундаментальную системурешений уравнения (2)).

Пример 2. Частные решения у₁(х) = sin x и у₂(х) = cos x, у₃(х) = 2sin x и у₄(х) = 5cos x (их бесчисленное

множество) уравнения у′′ + у = 0 образуют фундаментальную систему решений.

Решения у₅(х) = 0 и у₆(х) = cos x – не образуют.

Общим решением уравнения у′′ + у = 0 является функция у = С₁sin x + С₂cos x.

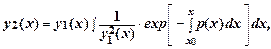В некоторых случаях удается тем или иным способом (например, подбором) найти только одно частное решение у₁(х). Тогда второе частное решение у₂(х) можно найти по формуле

где х₀Î[a, b]. Оба решения у₁(х) и у₂(х) при этом линейно независимы.

Замечание. Сказанное выше распространяется на линейные однородные диф.уравнения n-го порядка

y⁽ⁿ⁾ + a₁(x) y^{(n – 1)} + a₂(x) y^{(n – 2)} + … + a_n(x) y = 0. (4)

1. Если функции у₁ = у₁(х), у₂ = у₂(х), … , у_n = у_n (х) являются частными решениями уравнения (4), то

его решением является и функция у = С₁ у₁ + С₂ у₂ + … + С_n у_n .

2. Функции у₁, у₂, … , у_n называются линейно независимыми на (a, b), если равенство

α₁ у₁ + α₂ у₂ + … + α_n у_n = 0 выполняется лишь в случае, когда α₁ = α₂ = … = α_n = 0. Если хотя бы

одно из чисел α_i ( i = 1, 2, … , n ) отлично от нуля, функции у₁, у₂, … , у_n являются линейно

зависимыми.

3. Определитель Вронского имеет вид W(x) = .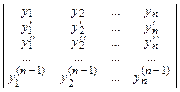

4. Частные решения у₁, у₂, … , у_n уравнения (4) образуют фундаментальную систему решений на

(a, b), если ни в одной точке этого интервала вронскиан не обращается в нуль, т.е. W(x) ≠ 0 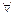х 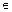(a, b).

5. Общее решение линейного однородного дифференциального уравнения (4) имеет вид

у = С₁ у₁ + С₂ у₂ + … + С_n у_n ,

где C_i (i = 1, 2, … , n) – произвольные постоянные, у_i – частные решения уравнения (4),

образующие фундаментальную систему.