Второго порядка с постоянными коэффициентами

Рассмотрим линейное однородное диф.уравнение (ЛОДУ) второго порядка с постоянными коэффициентами

y¢¢ + py¢ + qy = 0, (4)

где p иq – const.

Для нахождения общего решения ДУ (4) достаточно, согласно теореме 4, найти два его частных решения, образующих фундаментальную систему решений. Покажем, что частное решение может иметь вид у = e^kx. Имеем: y′ = k e^kx, y′′ = k ²e^kx. Подставляем у, y′, y′′ в (4) и получим k ²e^kx + p k e^kx + q e^kx = e^kx (k² + pk + q) = 0. Т.к. e^kx ≠ 0, то при k, обращающем в нуль квадратный трехчлен k² + pk + q, e^kx является решением уравнения (4).

Квадратное уравнение

k² + pk + q = 0 (5)

называется характеристическим уравнением для уравнения (4). Для его составления достаточно в уравнении (4) заменить y′′, y′ и y соответственно на k², k и1.

Для составления общего решения у_оо диф.уравнения (4) необходимо найти корни соответствующего характеристического уравнения (5) и применить следующую теорему:

Случай 1. Корни k₁ и k₂ уравнения (5) действительные и различные: k₁ ¹ k₂ , (D = p² – 4q > 0).

В этом случае частными решениями являются функции у₁ = e^{k1 x} и у₂ = e^{k2 x} . Они образуют

ФСР. Следовательно, общее решение уравнения (4), согласно теореме 4, имеет вид:

у_оо = С₁ e ^k1х + С₂ e ^{k2 x} .

Пример 1. Решить уравнение у′′ – 5у′ + 6у = 0.

Составим характеристическое уравнение k² – 5k + 6= 0. Решаем его: k₁ = 2, k₂ = 3. Записываем

общее решение исходного уравнения у_оо = С₁ e^2х + С₂ e^3х .

Случай 2. Корни k₁ и k₂ уравнения (5) действительные и равные: k₁ = k₂ = k , (D = p² – 4q = 0).

В этом случае имеем лишь одно частное решение у₁ = e ^kx. Второе частное решение имеет

вид у₂ = хe ^{k x} . Частные решения у₁ = e ^kx и у₂ = хe ^{k x} образуют ФСР. Общее решение

уравнения (4) имеет вид:

у_оо = С₁ e ^kх + С₂ хe ^{k x} .

Пример 2. Решить уравнение у′′ – 4у′ + 4у = 0.

Составим характеристическое уравнение k² – 4k + 4= 0. Решаем его: k = 2 – двукратный корень.

Записываем общее решение исходного уравнения у_оо = С₁ e^2х + С₂ хe^2х = e^2х (С₁ + С₂ х).

Случай 3. Корни k₁ и k₂ комплексные: k₁ = α + βi, k₂ = α – βi (D = p² – 4q < 0).

В этом случае частными решениями уравнения (4) являются функции у₁ = e ^{(α + βi ) x} и

у₂ = e ^{(α – βi ) x}. По формулам Эйлераe ^iφ = cos φ + i sin φ, e ^{–i φ} = cos φ – i sin φ имеем:

у₁ = e ^αx ∙ e ^{i β х} = e ^αxcos βx + i e ^αxsin βx,у₂ = e ^αx ∙ e ^{–i β х} = e ^αxcos βx – i e ^αxsin βx.

Составим две линейные комбинации решений у₁ и у₂: 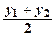= e ^αxcos βx = 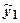и

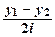= e ^αxsin βx = 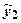. Функци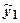и и 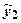также являются решениями уравнения (4), что следует из теоремы 1. Они образуют ФСР. Поэтому общее решение уравнения (4) запишется в виде

у_оо = С₁ e ^αxcos βx + С₂ e ^αxsin βx или у_оо = e ^αx(С₁ cos βx + С₂ sin βx).