Метод вариации произвольных постоянных нахождения общего решения

Общее решение у_онуравнения (1) можно найти, если известно общее решение у_оосоответствующего однородного уравнения (2) методом вариации произвольных постоянных (методом Лагранжа), состоящем в следующем.

Пусть у_оо = С₁ у₁(х) + С₂ у₂(х) –общее решение уравнения (2). Частное решение у_чуравнения (1) ищем в виде

У_он= С₁(х) у₁(х) + С₂(х) у₂(х). (3)

Функция (3) будет общим решением уравнения (1), если функции С₁(х) иС₂(х)удовлетворяют системе уравнений 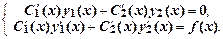(4)

Определитель системы 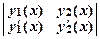≠ 0, т.к. это вронскиан для ФСР у₁(х)иу₂(х)уравнения (2). Поэтому система (4) имеет единственное решение: С′₁(х) = φ₁(х)и С′₂(х) = φ₂(х),где φ₁(х)и φ₂(х) – некоторые функции от х. Интегрируя эти функции, находим С₁(х) иС₂(х), а затем по формуле (3) составляем общее решение уравнения (1).

Пример 2. Найти общее решение уравнения у′′ + у = .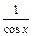

Найдем общее решение у_оо соответствующего однородного уравнения у′′ + у = 0. Имеем: k² + 1 = 0=>

k₁ = i, k₂ = –i => у_оо = C₁cos x + C₂ sin x. Найдем теперь общее решение у_он исходного уравнения. Оно ищется в виде у_он = C₁(х) cos x + C₂ (х) sin x. Для нахождения C₁(х) и C₂ (х) составим систему (4): 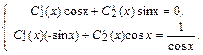Решим ее с помощью формул Крамера: Δ = 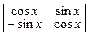= cos²x + sin²x = 1;

Δ₁ = 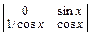= –tg x; Δ₂ = 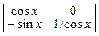= 1 => C′₁(х) = 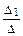= –tg x; C′₂(х) = 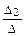= 1. Интегрируем эти равенства: С₁(х) = 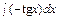= ln | cos x | + С₁; С₂(х) = 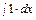= x + С₂. Следовательно, общее решение у_он данного уравнения у_он =(ln | cos x |+ С₁)∙ cos x + (x + С₂) sin x.

При нахождении частных решений ЛНДУ может быть полезной следующая теорема:

Теорема 7 (о наложении решений). Если правая часть уравнения (1) представляет собой

сумму двух функций f (x) = f₁(x) + f₂(x), а у_ч1 и у_ч2 – частные решения уравнений

y¢¢ + p (х) y¢ + q(х) y = f₁(х) и y¢¢ + p (х) y¢ + q(х) y = f₂(х)

соответственно, то функция у_ч = у_ч1 + у_ч2 является решением данного уравнения.