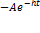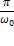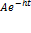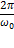Затухающим движением.

Объяснить это можно тем, что влияние силы

сопротивления, которая тормозит движение, настолько

превышает влияние силы обновления, которая вызывает

движение, что движение затихает раньше, чем материальная

точка перейдет положение равновесия.

② Коэффициент сопротивления равен коэффициенту обновления: h = ω. Тогда общее решение уравнения (2) имеет вид

x(t)

t

h < ω

O

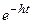x = (C₁ + C₂ t ).

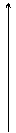Такое движение также называется апериодическим. Оно не отличается

от предыдущего в том смысле, что x(t) → 0 при t → +∞.

③ Коэффициент сопротивления меньше коэффициента

обновления: h < ω. В этом случае общее решение уравнения (2)

имеет вид

x = 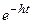(C₁ sin 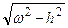t + C₂ cos 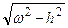t ). (3)

Если положить C₁ = А cos φ₀, C₂ = А sin φ₀, ω₀ = 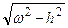, то решение (3) примет вид

x = А 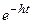sin(ω₀ t + φ₀). (4)

Теперь уже точка действительно совершает колебания – так называемые затухающие гармонические колебания. Величина А называется начальной амплитудой, ω₀ = 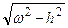– частотой, T = 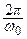– периодом, а φ₀ – начальной фазой затухающие гармонических колебаний.

Если коэффициент сопротивления h = 0, то

x = А sin(ω t + φ₀), (5)

т.е. материальная точка выполняет обычные гармонические колебания. Т.о., точка движется к

равновесию, но не монотонно, как в предыдущих случаях, а колеблясь около положения

равновесия с постепенно затухающими амплитудами.

Схематичный график затухающего гармонического колебания (при φ₀ = 0) изображен на

рисунке.

Значения постоянных C₁ и C₂ в формуле (3) или А и φ₀ в формуле (4) определяются из

начальных условий – начального отклонения точки и ее скорости.