Вынужденные колебания. Резонанс

Пусть в уравнении (1) внешняя сила φ(t) 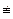0, тогда движение точки описывается линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Общее решение этого уравнения в квадратурах можно найти методом вариации произвольных постоянных.

Рассмотрим случай, когда движение происходит в среде без сопротивления и на колебательную систему действует периодическая внешняя сила φ(t) = H sin ω₁ t , тогда уравнение (1) принимает вид

x´´ + ω²x = H sin ω₁ t . (6)

Общим решением этого уравнения является сумма общего решения x_оо(t) соответствующего однородного уравнения и какого-нибудь частного решения x_чн(t) неоднородного уравнения (6).

Из формулы (5) вытекает, что общее решение x_оо(t) = А sin(ω t + φ₀). Чтобы найти частное решение x_чн(t) рассмотрим два случая.

① Нерезонансный случай: предположим, что ω ≠ ω₁, т.е. частота внешней силы отлична от частоты свободных колебаний. Т.к. число i ω₁ не совпадает с корнями ±i ω характеристического уравнения k² + ω² = 0, то частное решение следует искать в виде (правая часть имеет «специальный» вид)

x_чн(t) = a cos ω₁ t + b sin ω₁ t.

После нахождения методом неопределенных коэффициентов a и b , получим

x_чн(t) = 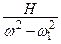sin ω₁ t,

тогда общее решение уравнения (6) имеет вид

x(t)= А sin(ω t + φ₀) + 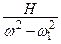sin ω₁ t.

Т.о., частное решение x_чн(t) определяет колебания точки, обусловленное внешней силой, общее решение x_оо(t) – свободные колебания, а общее решение x(t) – колебательные движения, образуемые в результате сложения двух колебаний с разными частотами ω и ω₁. В случае, когда ω и ω₁ мало отличаются друг от друга, материальная точка выполняет колебания с большой постоянной амплитудой.

② Резонансный случай: пускай теперь ω = ω₁, т.е. частота внешней силы равна частоте свободных колебаний. Т.к. i ω₁ совпадает с корнем i ω характеристического уравнения, то частное решение следует искать в виде (правая часть имеет «специальный» вид)

x_чн(t) = t (a cos ω t + b sin ω t).

Находя коэффициенты a и b , получим решение x_чн(t) = – cos ω t, поэтому общее решение уравнения (6) имеет вид

x(t)= А sin(ω t + φ₀) – cos ω t.

Из этой формулы вытекает, что, как и в предыдущем случае, имеем колебательное движение, которое получается в результате сложения двух колебаний, но с одинаковыми частотами. Второе слагаемое общего решения показывает, что амплитуда колебаний неограниченно возрастает при неограниченном возрастании времени t , т.е. материальная точка через некоторое время будет колебаться с очень большой амплитудой, даже если амплитуда H внешней силы совсем маленькая. Это явление носит название резонанса. Т.о., резонанс при колебательном движении наступает в том случае, если частота свободных колебаний совпадает с частотой внешней силы. Резонанс играет важную роль в технике и физике. Каждое упругое тело (например, любое сооружение) имеет свою определенную присущую ей частоту колебаний, которая зависит только от особенностей тела. Предположим, что это тело под действием внешней силы выводится из состояния равновесия. Если наступает явление резонанса, то действие силы, какой бы малой она не была, может привести к разрушению колебательной системы. Поэтому при проектировании различных сооружений (зданий, машин, мостов, самолетов, кораблей и т.д.) особое внимание обращают на расчеты мощности сооружения, связанные с резонансом.