Коэффициентами и правой частью специального вида

Рассмотрим ЛНДУ 2-го порядка с постоянными коэффициентами, т.е. уравнение

y¢¢ + p y¢ + q y = f (х),(5)

где p и q – действительные числа. Для таких уравнений существует более простой, чем метод вариации постоянных, способ нахождения частного решения у_ч, если правая часть f (х)уравнения (5) имеет т.н. «специальный вид». Суть метода, называемого методом неопределенных коэффициентов, состоит в следующем: по виду правой части f (х)уравнения (5) записывают ожидаемую форму частного решения с неопределенными коэффициентами, затем подставляют ее в уравнение (5) и из полученного тождества находят значения этих коэффициентов. Этот метод называется также методом подбора частного решения неоднородного уравнения и сводится к следующим двум случаям.

Случай 1. f (х)= e ^{a x}P_n (x), где P_n (x) –многочлен степениn.

Частные случаи: f (х)= P_n (x) (a = 0); f (х)= Сe ^{a x}, f (х)= e ^{a x}(n = 0, P₀ (x) = С = const,

в т.ч. С = 1 – многочлен 0-й степени); f (х)= С, f (х)= 1 (a = 0, n = 0).

Уравнение (5) имеет вид

y¢¢ + p y¢ + q y = e ^{a x}P_n (x). (6)

Частное решение у_ч ищем в виде

у_ч = x ^re ^axQ_n (x),

где r – число, равное кратности aкак корня характеристического уравнения k²+ p k + q = 0(т.е., r – число, показывающее, сколько раз a является корнем уравнения k²+ p k + q = 0), а

Q_n (x) = А₀ xⁿ + А₁ x^{n – 1} + … + A_n –многочлен той же степени n, что и P_n (x),записанный с неопределенными коэффициентами A_i (i = 0, 1, 2, … , n).

а) если a не является корнем характеристического уравненияk²+ p k + q = 0 (r = 0), то частное решение у_ч ищется в виде

у_ч = e ^{a x}Q_n (x) = e ^{a x} (А₀ xⁿ + А₁ x^{n – 1} + … + A_n). (7)

Для нахождения коэффициентами A_i продифференцируем у_ч два раза:

(у_ч)′ = e ^{a x} [nА₀ x^{n – 1}+ (n – 1)А₁ x^{n – 2} + … + A_{n – 1}] + α e ^{a x} (А₀ xⁿ + А₁ x^{n – 1} + … + A_n);

(у_ч)′′ = e ^{a x} [n(n – 1)А₀ x^{n – 2}+ (n – 1) (n – 2)А₁ x^{n – 3} + … + 2A_{n – 2}] +

+ 2α e ^{a x} [nА₀ x^{n – 1}+ (n – 1)А₁ x^{n – 2} + … + A_{n – 1}] + α² e ^{a x} (А₀ xⁿ + А₁ x^{n – 1} + … + A_n).

Подставим функцию у_ч и ее производные (у_ч)′ и (у_ч)′′ в уравнение (6), сократим на e ^{a x} и в результате получим:

n(n – 1)А₀ x^{n – 2}+ (n – 1) (n – 2)А₁ x^{n – 3} + … + 2A_{n – 2} + 2α [nА₀ x^{n – 1}+ (n – 1)А₁ x^{n – 2} + … + A_{n – 1}] +

+ α²(А₀ xⁿ + А₁ x^{n – 1} + … + A_n) + p [nА₀ x^{n – 1}+ (n – 1)А₁ x^{n – 2} + … + A_{n – 1} + α (А₀ xⁿ + А₁ x^{n – 1} + … + A_n)] +

+ q(А₀ xⁿ + А₁ x^{n – 1} + … + A_n) = P_n (x).

Слева – многочлен степени n с неизвестными (неопределенными) коэффициентами, справа – многочлен степени n, но с известными коэффициентами. Приравнивая коэффициенты при одинаковых степенях х, получим систему n + 1 алгебраических уравнений для определения коэффициентов А₀, А₁,…, А_{n – 1} ,A_n.

Пример 1. Найти общее решение уравнения у′′ –2y′ + у = х – 4.

1) Найдем общее решение у_оо соответствующего однородного уравнения у′′ –2y′ + у = 0. Характеристическое уравнение k² –2k +1= 0 имеет корень k = 1 кратности r = 2. Следовательно,

у_оо = С₁е^х + С₂хе^х.

2) Правая часть исходного уравнения f (x)= х – 4 = е^{0 ∙ x}(х – 4) имеет «специальный» вид Р₁(х) ∙ е^{0 ∙ x},

причем α = 0 не является корнем характеристического уравнения: α = 0 ≠ 1. Поэтому, согласно формуле (7), частное решение ищем в виде у_ч = Q₁(х) ∙ е^{0 ∙ x} или у_ч = Ах + В, где А и В – неопределенные коэффициенты.

Тогда (у_ч)′ = А, (у_ч)′′ =0. Подставляя у_ч , (у_ч)′ и (у_ч)′′ в исходное уравнение, получим –2А + Ах + В = х – 4,

или Ах + (–2А + В)= х – 4. Приравнивая коэффициенты при одинаковых степенях х, получим систему уравнений

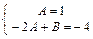=> A = 1, B = –2. Поэтому частное решение исходного уравнения у_ч = х –2. Следовательно,

3) у = у_оо + у_ч = С₁е^х + С₂хе^х + х –2– искомое решение.

б) если a – простой (однократный) корень характеристического уравнения

k²+ p k + q = 0 (r = 1),то частное решение у_ч ищется в виде у_ч = xe ^{a x}Q_n (x).

в) если a – двукратныйкорень характеристического уравненияk²+ p k + q = 0 (r = 2),то частное решение у_ч ищется в виде у_ч = x ²e ^{a x}Q_n (x).

Случай 2. f (х)= e^{a x} [ P_n (x) cosbx + Q_m (x) sinbx], где P_n (x)иQ_m (x) –многочлены степениn и m соответственно; α и β –действительные числа.

Частные случаи:

1) f (х)= P_n (x) cosbx + Q_m (x) sinbx, f (х)= P_n (x) cosbx, f (х)= Q_m (x) sinbx (α = 0);

2) f (х)= e^{a x} (С₁cosbx + С₂sinbx), f (х)= e^{a x}(cosbx + sinbx), f (х)= e^{a x} С₁cosbx,

f (х)= e^{a x} cosbx, f (х)= e^{a x} С₂sinbx, f (х)= e^{a x} sinbx (n = m =0,P₀ (x) = С₁ = const,

Q₀ (x) = С₂ = const,в т.ч.С_i = 1,–многочлен 0–й степени)

3) f (х)= С₁cosbx + С₂sinbx, f (х)= С₁cosbx, f (х)= С₂sinbx, f (х)= cosbx, f (х)= sinbx

(α = 0,n = 0).

Уравнение (5) в этом случае имеет вид

y¢¢ + p y¢ + q y = e ^{a x}[ P_n (x) cosbx + Q_m (x) sinbx]. (8)

Частное решение у_ч ищем в виде

у_ч = x ^re ^{a x}[ R_j (x) cosbx + S_j (x) sinbx], (9)

где r – число, равное кратности a + i bкак корня характеристического уравнения k²+ p k + q = 0,

R_j (x)иS_j (x)–многочлены степениj с неизвестными коэффициентами, j = max(n, m).

а) если a + i b не является корнем характеристического уравненияk²+ p k + q = 0

(r = 0), то

у_ч = e ^ax[ R_j (x) cosbx + S_j (x) sinbx]. (10)

б) если a + i b – корень уравнения k²+ p k + q = 0, то

у_ч = xe ^ax[ R_j (x) cosbx + S_j(x) sinbx], (11)

В частности, если f (х)= a cosbx + b sinbx,т.е. a = m = n = 0, то у_ч ищется в виде

у_ч = A cosbx + B sinbx(если число i b не является корнем характеристического уравнения), или в виде у_ч = x(A cosbx + B sinbx)(если число i b – корень характеристического уравнения).

Замечание. Ожидаемые многочлены Q_n (x)должны быть полными, т.е. содержать все степени хот 0 до n, независимо от того, является ли полным заданный многочлен Р_n (x).То же самое относится и к многочленам R_j (x)и S_j (x),причем неопределенные коэффициенты при одних и тех же степенях ху этих многочленов должны быть разными.

Пример 2. Найти общее решение уравнения у′′ –4y′ +13у = 40cos3х.

1) Найдем общее решение у_оо соответствующего однородного уравнения у′′ –4y′ +13y = 0. Характеристическое уравнение k² –4k +13= 0 имеет корни k₁ = 2 + 3i, k₂ = 2 – 3i . Следовательно,

у_оо = е^2x (С₁cos3x + С₂ sin3x).

2) Правая часть исходного уравнения f (x)=40cos3х = е^{0 ∙ x} ∙ 40cos3х имеет «специальный» вид

f (x)= е^{0 ∙ x} (40cos3х + 0 ∙ sin3x). Т.к. α = 0, β = 3, α + β i = 3i не совпадает с корнем характеристического уравнения, то r = 0. Поэтому, согласно формуле (10), частное решение ищем в виде у_ч = Аcos3х + В sin3x.

Тогда (у_ч)′ =–3Аsin3х + 3В cos3x, (у_ч)′′ =–9Аcos3х – 9 В sin3x. Подставляя у_ч , (у_ч)′ и (у_ч)′′ в исходное уравнение, получим –9Аcos3х – 9 В sin3x – 4 (–3Аsin3х + 3В cos3x) + 13 (Аcos3х + В sin3x) =40cos3х или

(–9А – 12B + 13A)cos3х + (–9B + 12A + 13B)sin3х =40cos3х. Приравнивая коэффициенты при одинаковых косинусах и синусах, получим систему уравнений

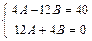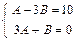=> A = 1, B = –3. Поэтому частное решение исходного уравнения у_ч =cos3х –3 sin3x. Следовательно,

3) у = у_оо + у_ч = е^2x (С₁cos3x + С₂ sin3x) + cos3х –3 sin3x – искомое решение.

2.10. Интегрирование ЛНДУ n-го порядка

Рассмотрим ЛНДУ n-го порядка, т.е. уравнение

y⁽ⁿ⁾ + a₁(x) y^{(n – 1)} + a₂(x) y^{(n – 2)} + … + a_n(x) y = f (х),(12)

где a₁(x), a₂(x), … , a_n(x)– заданные непрерывные на интервале (a, b) функции. Соответствующее ЛОДУ имеет вид

y⁽ⁿ⁾ + a₁(x) y^{(n – 1)} + a₂(x) y^{(n – 2)} + … + a_n(x) y =0.(13)

Общее решение у_онуравнения (12) можно найти, если известно общее решение у_оосоответствующего однородного уравнения (13) методом вариации произвольных постоянных (методом Лагранжа), состоящем в следующем.

Пусть

у_оо = С₁ у₁(х) + С₂ у₂(х) + … + С_n у_n(х)

(где у₁(х),у₂(х),…, у_n(х) –частные решения,образующие фундаментальную систему решений однородного уравнения (13)), –общее решение уравнения (13). Общее решение у_онуравнения (12) ищем в виде

у_он= С₁(х) у₁(х) + С₂(х) у₂(х) + … + С_n (х) у_n(х). (14)

Функция (14) будет общим решением уравнения (12), если функции С₁(х),С₂(х), … , С_n (х)удовлетворяют системе уравнений 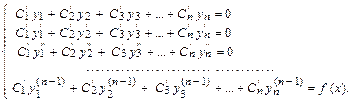(15)

Однако, для некоторых типов уравнений, например, для тех, правая часть которых имеет т.н. «специальный вид», у_он можно найти, основываясь на следующей теореме:

Частное решениеу_ч может быть найдено методом неопределенных коэффициентов.

Метод подбора частного решения у_чуравнения

y⁽ⁿ⁾ + p₁ y^{(n – 1)} + p₂ y^{(n – 2)} + … + p_n y = f (х),

где p_i, i = 1, 2, … , n – числа, а правая часть f (х) имеет специальный вид, описанный в п.2.9 для случая n = 2, переносится без всяких изменений и на случай уравнения, имеющего порядок n > 2.

Пример 3. Решить уравнение у^IV – y′ = 2х.

1) Находим у_оо: k⁴ – k = 0 => k (k – 1 ) (k² + k + 1) = 0 => k₁ = 0, k₂ = 1, k_3,4 = – =>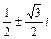

=> у_оо = С₁ + С₂е^х + .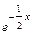

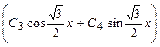2) Находим у_ч : f (x)= е^{0 ∙ x} (2х + 0) (= е^{0 ∙ x}∙ Р₁(х)) => r = 1, у_ч = х(Ах + В) = Ах² + Вx, (у_ч)′ =2Аx + B,

(у_ч)′′ =2A, (у_ч)′′′ =0, (у_ч)^IV=0 => –(2Аx + В)=2х => A = –1, B = 0=> у_ч =–х².

3) у = у_оо + у_ч = С₁ + С₂е^х + 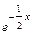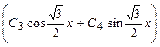– х² – общее решение исходного уравнения.