Важнейшие классы числовых функций одной переменной.

Напомним сначала основные элементарные функции:

линейная у = ах + b, в частности, у = b – постоянная функция;

квадратичная y = ax² + bx + c;

степенная 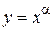, a ÎR;

показательная у = 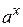, а > 0, а ¹ 1;

логарифмическая у = log _a x , а > 0, а ¹ 1;

тригонометрические у = sinx, y = cosx , y = tgx , y = ctgx ;

обратные тригонометрические функции у = arcsinx, y = arccosx ,

y = arctgx , y = arcctgx.

Определение 1. 5. Пусть у = f (u) и и = j(х) – функции, причем Е(j) Ì D(f). Тогда функция у = f (j(х)) называется функцией от функции или сложной функцией.

Например, y = sin²x Þ y = u², u = sinx;

.

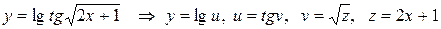Определение 1.6. Функция, получающаяся из основных элементарных функций путем применения к ним конечного числа арифметических действий и операции взятия функции от функции, называется элементарной функцией.

Например, у = х² + cos³e^-x, 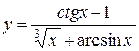– элементарные функции.

Функция вида 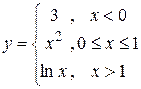не является элементарной.

Рассмотрим следующие классы функций.

I. Алгебраические функции. Алгебраическими функциями называют такие, которые могут быть решениями алгебраических уравнений. К ним относятся:

а) целые рациональные функции (многочлены)

Р(х) = а_пх^п + а_п-1х^п-1 + ... + а₁х + а ₀,

где а_п, а_п-1, ..., а₁, а₀ – действительные числа. В частности, целыми рациональными функциями являются линейная, квадратичная, степенная при aÎN.

б) дробно-рациональные функции (рациональные дроби)

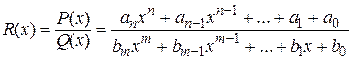
В частности, функция 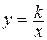– «обратная пропорциональность», дробно-линейная функция .

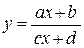в) иррациональные функции, которые получаются применением арифметических действий и взятия функции от функции к функциям вида .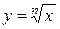

Например, .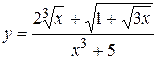

II. Трансцендентные функции – это те функции, которые не являются алгебраическими. К ним относятся логарифмические, показательные, тригонометрические, обратные тригонометрические функции.

III. Функции натурального аргумента – это функции, независимая переменная которых принимает значения из множества натуральных чисел N, при этом независимую переменную обычно обозначают п.

Например, S (n) = 1 + 2 + 3 + ... + n = ,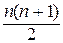

п! = 1.2.3.....п (факториал)

Обозначают функцию натурального аргумента f (n) , x_n, a_n . В последних двух случаях эту функцию называют функцией индекса.

Примером функции индекса является последовательность {a_n}, значения функции a_n при этом называют членами последовательности: а₁ – первый член последовательности, а₂ – второй, ..., а_п – п-й член последовательности. Такая функция считается заданной, если указано правило (формула), связывающее индекс п со значением функции, т.е. соответствующим членом последовательности, или формула, связывающая несколько членов одной и той же последовательности (рекуррентная формула). Например, формула

а_п = 5^{п –1} , пÎN определяет последовательность 1, 5, 25, 125, ...;

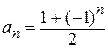, пÎN – последовательность 0, 1, 0, 1, ...;

а_п = 2а_п–1 – а_п–2 – последовательность 1, 0, –1, –2, –3, –4, ...