Вiльнi коливання матерiальної точки при наявностi опору

При невеликих швидкостях сила опору середовища прямо пропорцiональна швидкостi i напрямлена протилежно їй. Проекцiя сили опору на вiсь Ох дорівнює R_x=- 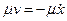(μ>0; знак ”мiнус” тому, що сила опору напрямлена протилежно до швидкостi). Коефiцiєнт μ дорiвнює силi опору при швидкостi руху точки, рiвнiй одиницi. Якщо на матерiальну точку дiють сила опору R_x = - 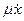i пружна сила F = - 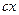, то рiвняння руху буде таким:

m =-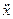

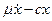
або

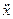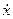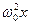+2n + =0, (5.10)

де n = μ/2m - показник затухання, μ - коефiцiєнт в’язкого опору, 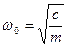- циклiчна частота власних коливань.

Одиниця вимiрювання показника затухання n – с^-1.

Для вiдповiдного характеристичного рiвняння маємо коренi:

;

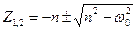а) у випадку, коли n<ω₀ (сила опору досить мала) загальний розв’язок рiвняння (5.10) має вигляд:

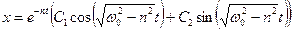(5.11)

або

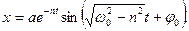. (5.12)

Рiвняння (5.12) показує, що амплiтуда ae^-nt коливань з часом зменшується. Такi коливання називаються затухаючими коливаннями, рiвняння (5.12) називають рiвнянням затухаючих коливань.

Циклiчна частота затухаючих коливань дорiвнює

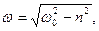(5.13)

перiод затухаючих коливань дорiвнює

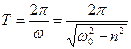. (5.14)

Ця формула доводить, що поява сил опору збiльшує перiод коливань. З погляду фiзики це зрозумiло: опiр уповiльнює рух. Сталi iнтегрування а i φ₀ обчислюють за формулами:

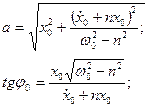
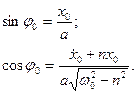(5.15)

Вiдношення двох послiдовних максимальних вiдхилень дорівнює:

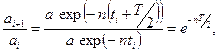(5.16)

де Т визначається формулою (5.14). Величина Δ = е^-nT/2 називається декрементом затухання; натуральний логарифм декремента, тобто величина -nТ/2, називається логарифмiчним декрементом затухання:

(5.17)

Декремент затухання характеризує швидкiсть затухання амплiтуди коливання;

б) у випадку, коли n>ω₀ (сила опору досить велика), коренi Z₁ i Z₂ дiйснi i рiзнi:

.

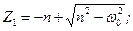
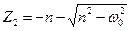Загальний розв’язок рiвняння (5.10) в цьому випадку такий:

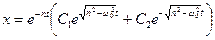(5.18)

або

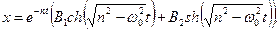(5.19)

де

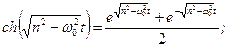
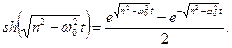
В деяких випадках розв’язок (5.19) можна подати у виглядi:

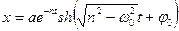; (5.20)

змiщення х асимптотичнo прямує до нуля, коли t→∞. При досить великiй силi опору рух не є коливальним. Такий рух називають аперiодичним затуханням;

в) у випадку, коли n = ω₀ (особливий випадок), корені Z₁ і Z₂ однакові та від’ємні Z₁=Z₂= -n і загальний розв’язок рiвняння (5.10) такий:

x = e^-nt(C₁t + C₂) . (5.21)

Вiдповiдний рух зводиться до аперiодичного затухання.

На використаннi закономiрностей затухаючих коливань працюють демпфери, що бувають рiзних систем i вiдiграють роль глушителiв шкiдливих механiчних i електричних коливань.

Зауваження. Для закріплення матеріалу §5 (пунктів 5.1 і 5.2) необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 32.1, 32.2, 32.5, 32.6, 32.12, 32.15, 32.24, 32.26, 32.28, 32.60, 32.70, 32.77;

2) № 32.4, 32.13, 32.14, 32.16, 32.18, 32.30, 32.36, 32.53, 32.59, 32.65, 32.66, 32.68, 32.69, 32.71;

3) №32.38, 32.41, 32.43, 32.46, 32.49, 32.74, 32.75, 32.76.

Рекомендується розв’язати також задачі № 659, 660, 669, 672, 674 зі збірника “Сборник задач по теоретической механике /Под ред. М. А. Бражниченко. – М., Высшая школа, 1986”.

Питання для самоконтролю

1. Які рухи і процеси відносять до коливань?

2. Які коливання називають періодичними?

3. Що називають періодом коливань і частотою коливань?

4. Назвіть одиницю вимірювання частоти коливань і поясніть її фізичну суть.

5. Який вид періодичних коливань є найбільш важливим? Наведіть приклади таких коливань.

6. Запишіть і розв’яжіть диференціальне рівняння руху тягаря на пружині.

7. Як записується закон вільних коливань тягаря на пружині при відсутності опору?

8. Назвіть початкові умови руху тягаря на пружині при відсутності опору. Як в цьому випадку визначаються сталі інтегрування?

9. Що називають амплітудою коливань?

10. Яку величину називають миттєвою фазою коливань, а яку – початковою фазою?

11. Як визначити період коливань?

12. Від чого залежить період вільних незатухаючих коливань матеріальної точки?

13. Яку величину називають циклічною частотою коливань? Поясніть її фізичну суть.

14. Як змінюються швидкість та прискорення тіла, що здійснює гармонічні коливання?

15. Як пов’язані між собою фази координати, швидкості та прискорення гармонічних коливань у випадку відсутності опору?

16. Якою є сила опору середовища при невеликих швидкостях руху і як визначається її проекція на вісь руху?

17. Поясніть фізичну суть коефіцієнта μ.

18. Запишіть диференціальне рівняння руху матеріальної точки у випадку дії сили опору і пружної сили одночасно.

19. Якими будуть корені характеристичного рівняння при розв’язанні диференціальних рівнянь руху матеріальної точки при наявності сили опору?

20. Запишіть загальний розв’язок диференціального рівняння коливань матеріальної точки при дії сили опору, коли сила опору досить мала (n<ω₀).

21. Які коливання називають затухаючими? Напишіть рівняння затухаючих коливань.

22. Чому дорівнюють циклічна частота затухаючих коливань і період затухаючих коливань?

23. Як впливає поява сил опору на період коливань?

24. Запишіть формули, за якими обчислюють сталі інтегрування в рівнянні затухаючих коливань.

25. Чому дорівнює відношення двох послідовних максимальних відхилень?

26. Що називають декрементом затухання та логарифмічним декрементом затухання?

27. Що характеризує декремент затухання?

28. Якими будують корені характеристичного рівняння при розв’язанні диференціального рівняння коливального руху матеріальної точки при наявності сил опору, якщо сила опору досить велика (n>ω₀)?

29. Запишіть загальний розв’язок диференціального рівняння коливального руху у випадку великого опору.

30. Як називають рух матеріальної точки при наявності великого опору?

31. Запишіть загальне розв’язання диференціального рівняння коливального руху матеріальної точки при наявності сили опору, коли n=ω₀.

32. Як практично використовуються закономірності затухаючих коливань? Наведіть приклади.