С бесконечно высокими стенками

Потенциальная яма	Потенциальная энергия	Стационарное уравнение Шредингера в пределах ямы ( )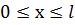
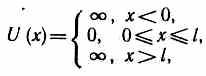
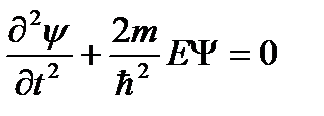		или

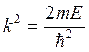
L -ширина ямы, энергия отсчитывается от дна ямы, k- волновое число; E- полная энергия частицы.

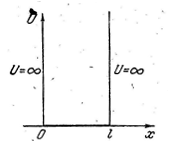
Т.е. такая «яма» описывается потенциальной энергией указанного вида (для простоты принимаем, что частица движется вдоль оси х).

Граничные условия: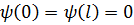

Это следует из условия непрерывности. За пределы ямы частица не проникает, и в областях х < 0 и х > 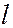волновая функция y(х)=0.

Общее решение дифференциального уравнения:

y(х)=Аsinkx+Bcoskx

Так как y (0)= y(l)=0, то В=0.

Условие y (l)=Asinkl=0 выполняется только при kl = np, n— целые числа, т. е. необходимо, чтобы

k= np/l (n=1,2,3…)

Подставив значение k , найдем собственные функции:

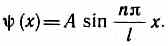
Постоянную интегрирования А найдем из условия нормировки, которое для данного случая запишется в виде

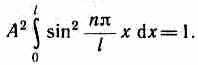
В результате интегрирования получим 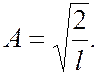, а собственные функции будут иметь вид

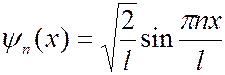, (n=1,2,3…)

Собственные значения энергии частицы получаются из выражений 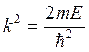и k= np/l :

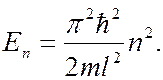(n=1,2,3…)

Т.е. спектр энергии частицы дискретен.

Квантованные значения E_n- уровни энергии; n- квантовое число.

Минимальная, не равная нулю энергия, соответствующая основному состоянию:

E₁=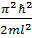

Наличие отличной от нуля минимальной энергии – следствия соотношения неопределенностей.

Неопределенность координаты 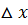частицы в яме шириной l равна 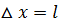. Неопределенность импульса Dp_x » h/ l (частица «зажата» в яме, следовательно, ее положение известно с неопределенностью 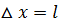), поэтому энергия нулю не может быть равна.

Состояние с энергией E₁- основное состояние, остальные состояния - возбужденные. Энергии возбужденных состояний: 4Е₁, 9E₁, 16E₁, … (соответственно значениям квантовых чисел n=2,3,4, … .)

Т. е. стационарное уравнение Шредингера, описывающее движение частицы в «потенциальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях E_n, зависящих от целого числа п.

Следовательно, энергия E_n частицы в «потенциальной яме» с бесконечно высокими «стенками» принимает лишь определенные дискретные значения, т. е. квантуется.

Квантованные значения энергии E_n называются уровнями энергии,а число n, определяющее энергетические уровни частицы, называется главным квантовым числом.Таким образом, микрочастица в «потенциальной яме» с бесконечно высокими «стенками» может находиться только на определенном энергетическом уровне E_n, или, как говорят, частица находится в квантовом состоянии п.

Графики собственных функций, соответствующие уровням энергии при n=1,2,3, приведены на рис. 7.6.1,а. На рис. 7.6.1,б изображена плотность вероятности y обнаружения частицы на различных расстояниях от «стенок» ямы, равная |y_n(x)|² для

n=1, 2 и 3. Из рисунка следует, что, например, в квантовом состоянии с n=2 частица не может находиться в середине «ямы», в то время как одинаково часто может пребывать в ее левой и правой частях. Такое поведение частицы указывает на то, что представления о траекториях частицы в квантовой механике несостоятельны.

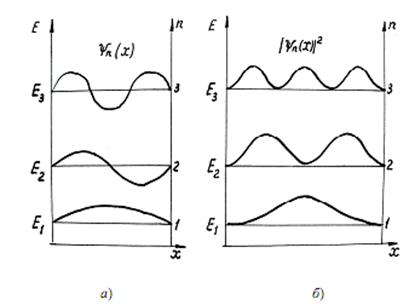Рис.7.6.1

Энергетический интервал между двумя соседними уровнями равен:

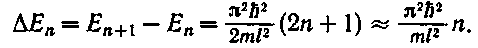
Например, для электрона при размерах ямы l =10^-1м (свободные электроны в металле) энергетические уровни расположены столь тесно, что спектр практически можно считать непрерывным. Если же размеры ямы соизмеримы с атомными, то для электрона получаются явно дискретные значения энергии (линейчатый спектр). Таким образом, применение уравнения Шредингера к частице в «потенциальной яме» с бесконечно высокими «стенками» приводит к квантованным значениям энергии, в то время как классическая механика на энергию этой частицы никаких ограничений не накладывает.

При больших квантовых числах n соседние уровни расположены тесно: тем теснее, чем больше п. Если n очень велико, то можно говорить о практически непрерывной последовательности уровней и характерная особенность квантовых процессов — дискретность — сглаживается. Этот результат является частным случаем принципа соответствия Бора, согласно которому законы квантовой механики должны при больших значениях квантовых чисел переходить в законы классической физики.