Конечной ширины. Туннельный эффект.

Если U₀ — высота потенциального барьера; Е — полная энергия частицы; m — масса частицы, то потенциальный барьер конечной ширины:

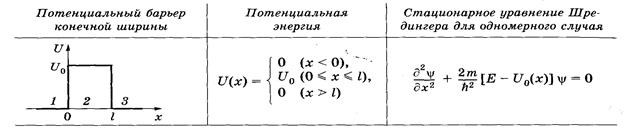
При данных условиях задачи классическая частица, обладая энергией Е, либо беспрепятственно пройдет над барьером (при Е > U₀), либо отразится от него (при Е < U₀) и будет двигаться в обратную сторону, т. е. она не может проникнуть сквозь барьер.

Для микрочастицы, даже при E > U₀, имеется отличная от нуля вероятность, что частица отразится от барьера и будет двигаться в обратную сторону. При E < U₀ имеется также отличная от нуля вероятность, что частица окажется в области х >L, т. е. проникает сквозь барьер. Подобные, казалось бы, парадоксальные выводы следуют непосредственно из решения уравнения Шредингера, описывающего движение микрочастицы при условиях данной задачи.

А) Энергия частицы больше высоты потенциального барьера (Е>Uo)

[k_1,3 = 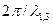и k₂ = 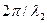— волновые числа; λ _{1, 3} и λ₂ — соответственно длины волн де Бройля в областях 1, 3 и 2]

Общие решения уравнений Шредингера:

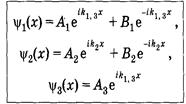
В области 3 имеется только прошедшая барьер волна, поэтому коэффициент В₃ принят равным нулю.

♦ е ^ikx соответствует плоской волне, распространяющейся в положительном направлении оси х (падающей волне), е ^-ikx— отраженной волне. О волнах может идти речь после умножения на временной множитель, так как Ψ— координатная часть волновой функции.

Коэффициент отражения 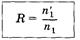Равен отношению плотности потока отраженных (n_1/) частиц к плотнос­ти потока падающих (n₁) частиц.

Коэффициент прозрачности 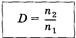Равен отношению плотности потока прошедших (п₂) частиц к плотности потока падающих (n₁) частиц.

Возможное определение коэффициентов отражения и прозрачности:

Вывод.В случае Е >U₀ волна на границе 1 и 2 частично отражается ( 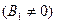и частично проходит в область 2, затем она опять на границе 2 и 3 частично отражается ( 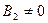) и частично проходит в область 3. В облас­ти 2 длина волны де Бройля больше, чем в областях 1 и З.

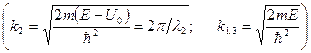
Итак, при E > U₀ имеем k_1,3 > k₂ и λ₂ > λ_1,3

Б)Энергия частицыменьше высоты потенциального барьера (Е < U₀)

Уравнение Шредингера:

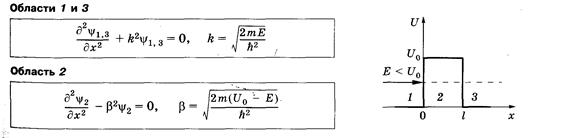
Общие решения уравнений Шредингера:

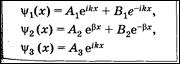
В области 2 решение Ψ₂ (х) не соответствует плоским волнам, распространяющимся в обе стороны (показатели экспонент не мнимые, а действительные).

В области 3 имеется только волна, прошедшая сквозь барьер и распространяющаяся слева направо, поэтому принято В₃ = 0. Из условий непрерывности волновой функции и ее первой производной в точках х = 0 и х = L можно найти коэффициенты А₂ и В₂. Можно показать, что для высокого и широкого барьера 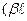»1) В₂ » А₂, а тогда на границе потенциального барьера, где х = 0, определяющим членом волновой функции Ψ₂ является член, содержащий В₂ .

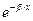Вывод. В случае Е < U₀, согласно квантовой механике, микрочастица может «пройти» сквозь потенциальный барьер. Это специфическое квантовое явление получило название туннельного эффекта.

Туннельный эффект

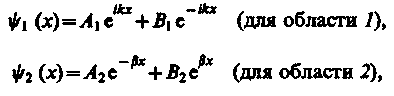
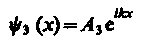(для области 3)

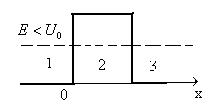Рис.7.7.1

Качественный характер функций y1(x), y2(x), y3(x) иллюстрируется на рис. 3, б, откуда следует, что волновая функция не равна нулю и внутри барьера, а в области 3, если барьер не очень широк, будет опять иметь вид волн де Бройля с тем же импульсом, т. е. с той же частотой, но с меньшей амплитудой. Следовательно, получили, что частица имеет отличную от нуля вероятность прохождения сквозь потенциальный барьер конечной ширины (Рис. Рис.7.7.2)

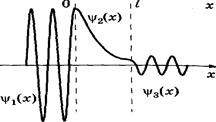
Рис.7.7.2

Выводы. Волновая функция не равна нулю и внутри барьера, а в области 3, если барьер не очень широк, будет опять иметь вид волн де Бройля с тем же импульсом, т. е. с той же частотой, но с меньшей амплитудой. Следовательно, частица имеет отличную от нуля вероятность прохождения сквозь по­тенциальный барьер конечной ширины — наблюдается туннельный эффект.

Для описания туннельного эффекта используют понятие коэффициента прозрачности D потенциального барьера, определяемого как отношение плотности потока прошедших частиц к плотности потока падающих.

Коэффициент прозрачности (вероятность проникновения сквозь потенциальный барьер конечной ширины)

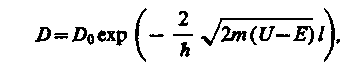
Коэффициент прозрачности D сильно зависит от массы частицы, быстро убывает с увеличением как ширины барьера, так и его высоты. Чем шире барьер, тем меньше вероятность прохождения сквозь него частицы.

[U_{0 (}U) — высота потенциального барьера; Е — энергия частицы; L — ширина прямо­угольного барьера; т — масса частицы; 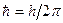— приведенная постоянная Планка; D₀ — по­стоянный множитель, который, как показывают точные расчеты, не очень отли­чается от единицы]

Коэффициент прозрачности для барьера произвольной формы

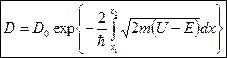
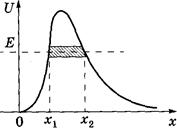
Рис.7.7.3

Эта формула — хорошее приближение в случае потенциального барьера произволь­ной формы, если барьер удовлетворяет ус­ловию квазиклассического приближения (достаточно гладкая форма кривой), обобщение формулы для D в случае прямоугольного барьера.

Выводы относительно поведения классической и квантовой частиц:

При Е < U₀ по классической теории частицы не смогут преодолеть потен­циального барьера и отразятся от него; согласно квантовой теории, часть частиц отражается, а часть имеет отличную от нуля вероятность пройти сквозь потенциальный барьер.

При Е > U₀,по классической теории все частицы преодолевают потенциальный барьер; согласно квантовой тео­рии, часть частиц проходит, а часть отражается. Как подбаръерное про­хождение, так и надбарьерное отражение являются специфическими квантовыми эффектами, связанными с волновыми свойствами частиц.