Атом водорода в квантовой механике

В квантовой механике задача об атоме водорода (помимо его простой структуры) является одной из основных еще и потому, что задача о движении электрона в поле центральных сил может быть распространена (естественно, с разной степенью приближения) на водородоподобные системы- системы, состоящие из ядра с зарядом Ze и одного электрона (например, He⁺, Li²⁺).

Состояние электрона в атоме водорода

Потенциальная энергия взаимодействия электрона с зарядом, обладающим зарядом Ze: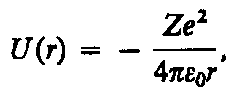

Стационарное уравнение Шредингера для электрона в атоме водорода:

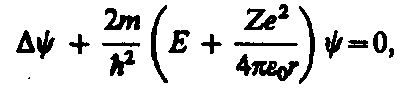
Это уравнение получается при подстановке в стационарное уравнение Шредингера.

(Z- порядковый номер элемента в таблице Менделеева, е - элементарный заряд; 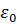-электрическая постоянная, r- расстояние между электроном и ядром; m- масса электрона, Е - полная энергия электрона в атоме; 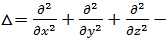оператор Лапласа; 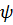- координатная часть волновой функции)

Энергия электрона в атоме водорода

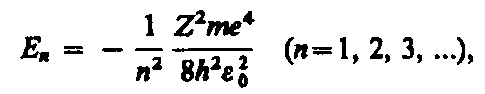
Решение уравнения Шредингера непрерывны, однозначны и конечны в случаях:

-при любых положительных значениях энергии (соответствует свободному электрону – заштрихованная область на рисунке);

-при дискретных отрицательных значениях энергии (соответствует получаемым из уравнения Шредингера собственным значениям энергии).

Собственные значения энергии в точности совпадают с уровнями энергии в модели атома Бора

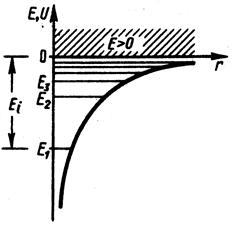
Возможные значения энергии:

Дискретные значения энергии E₁,E₂,E₃, …(на рисунке показаны в виде горизонтальных прямых)

Основной энергетический уровень- самый нижний уровень E_1., отвечающий минимальной возможной энергии.

Возбужденные энергетические уровни-

энергетические уровни E_n>E₁ (n=2,3, … .)

Связанное движение электронов:

Движение при Е<0 - электрон находится внутри гиперболической потенциальной ямы. По мере роста n энергетические уровни располагаются теснее и при n=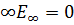

Энергия ионизации атома водорода - энергия, необходимая для отрыва электрона, находящегося в основном состоянии, от атома:

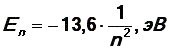
Квантовые числа

Уравнению Шредингера удовлетворяют собственные функции 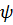_nlm( 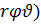, определяемые тремя квантовыми числами: главным n, орбитальным l, и магнитным m_l.

1) Главное квантовое число n совпадает с номером энергетического уровня, определяя энергию электрона в атоме, 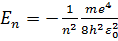и может только принимать целые положительные значения.

(n=1,2,3, … .)

2) Орбитальное квантовое число l определяет, согласно решению уравнения Шредингера, модуль момента импульса электрона (механический орбитальный момент)

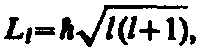
который может принимать лишь дискретные значения, т.е. квантуется. Орбитальное квантовое число l принимает всего n значений.

L=0,1,2, …,(n-1)

3) Магнитное квантовое число m₁ определяет, согласно решению уравнения Шредингера, проекцию момента импульса электрона на направление z внешнего магнитного поля

L_{lz= ,}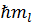

причем вектор момента импульса электрона в атоме может иметь в пространстве 2l+1 ориентаций (m_l принимает всего 2l+1 значений)

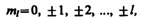
Хотя энергия электрона и зависит только от главного квантового числа п, но каждому собственному значению Еn (кроме Е1) соответствует несколько собственных функций 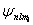, отличающихся значениями l и m_l. Следовательно, атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях. Число состояний с одинаковой энергией: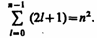

Т.е. кратность вырождения энергетических уровней атома водорода равна п²