Бесконечно большие функции и их связь с бесконечно малыми

Пусть функция 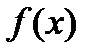определена в некоторой проколотой окрестности 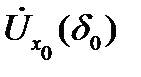точки

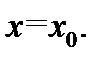
Определение 5. Функция 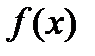называется бесконечно большой функцией (ББФ) при 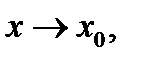если для всякого 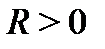существует число 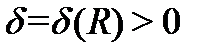такое, что

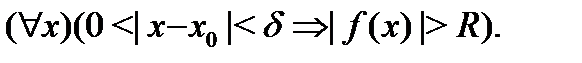
При этом пишут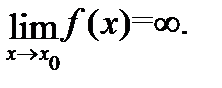

Заметим, что 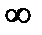– это не число, а символ, поэтому бесконечный предел – это всего лишь обозначение бесконечно большой функции. Тем не менее при вычислениях удобно относиться к бесконечному пределу как к обычному, хотя для бесконечных пределов и существуют свои правила действий, несколько отличные от правил действий над конечными пределами (см. ниже таблицу 2).

Если функция 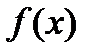сохраняет знак в некоторой проколотой окрестности точки 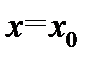и является при этом бесконечно большой функцией, то естественно писать

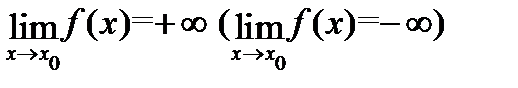
(в зависимости от знака функции 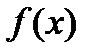в указанной окрестности). Более точно:

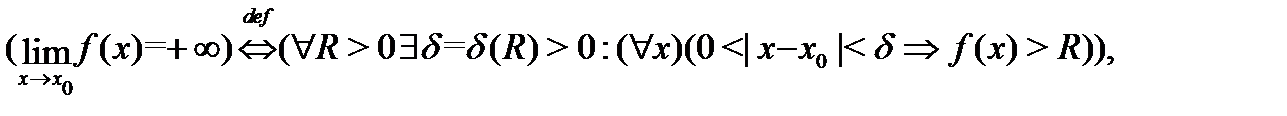
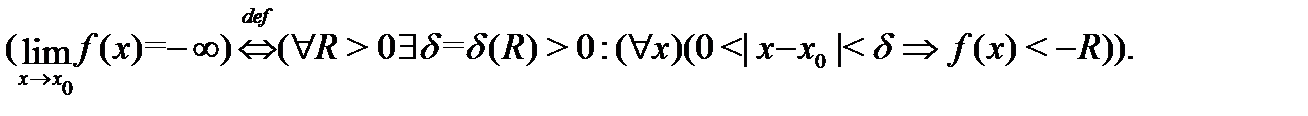
В этих определениях и определении 5 фигурирует окрестность

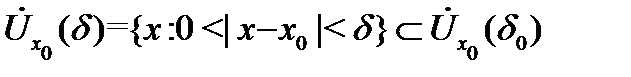
конечной предельной точки 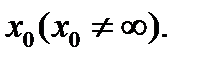Почти дословно определяются бесконечно большие функции на бесконечности. В этом случае под точкой 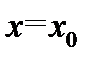следует понимать один из символов: 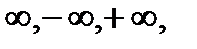а под окрестностью 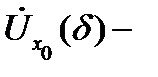окрестность соответствующей бесконечно удаленной точки 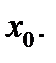Например,

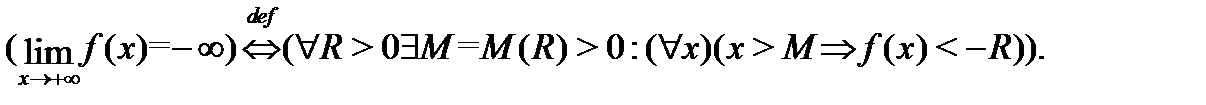
Нетрудно доказать следующее утверждение.

Теорема 7. Пусть функция 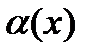не обращается в нуль в некоторой проколотой окрестност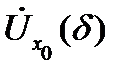и точки 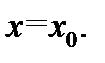Тогда справедливо высказывание

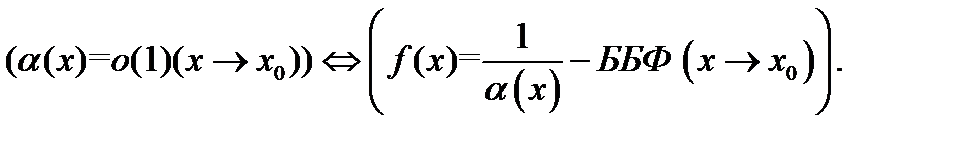
Иначе говоря, для того чтобы функция 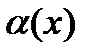была бесконечно малой при 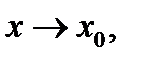необходимо и достаточно, чтобы обратная к ней по величине функция 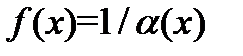была бесконечно большой при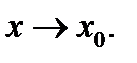

Используя эту теорему, можно доказать истинность следующих операций над бесконечно большими функциями:

Таблица 2

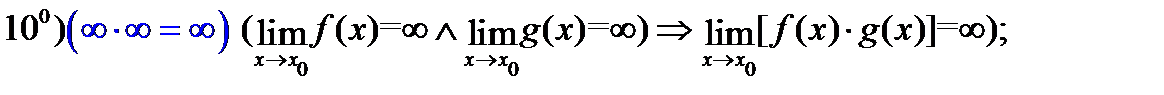
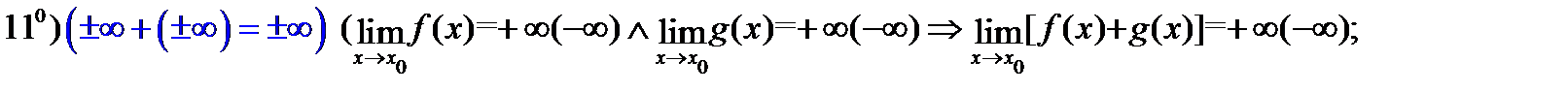
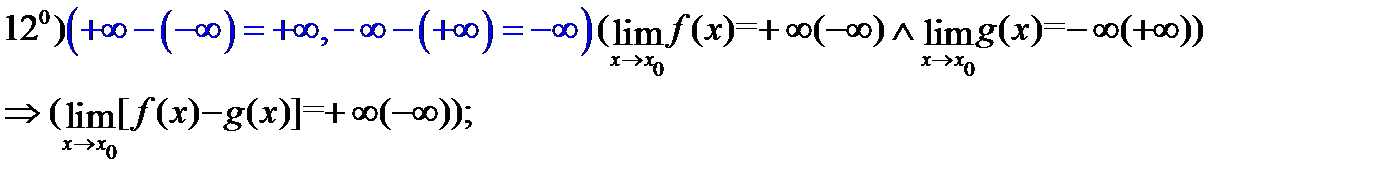
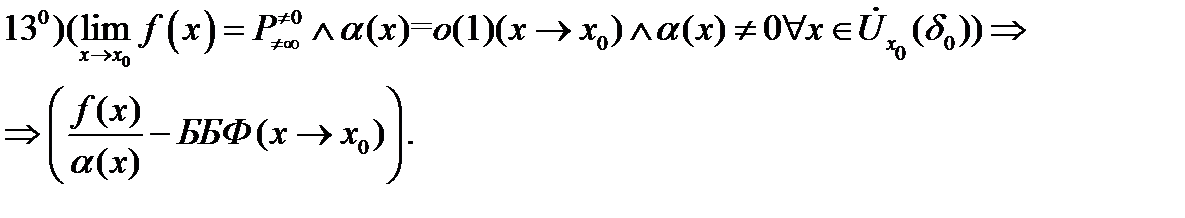
И, наконец, отметим ещё ряд свойств, связанных с пределами функций.

Теорема 7 (о пределе промежуточной функции). Пусть в некоторой окрестност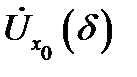и точки 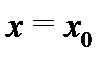выполняются неравенства 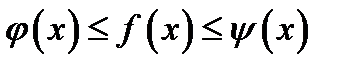и пусть, кроме того, крайние функции имеют пределы в точке 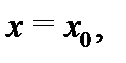и эти пределы равны друг другу, т.е.

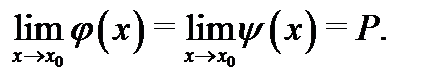
Тогда существует предел промежуточной функции и он равен 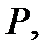т. е. 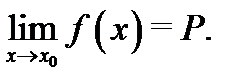Теорема 8. Пусть в некоторой окрестност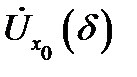и точки 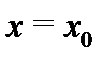выполняются неравенства 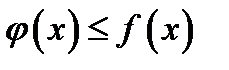и пусть существуют пределы

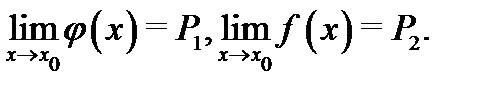
Тогда 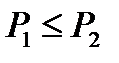(докажите это утверждение самостоятельно).

Теорема 9(о знаке предела). Если в некоторой проколотой окрестности 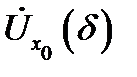функция 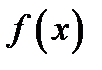неотрицательна (неположительна) и существует предел 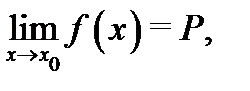то 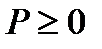(соответственно ).

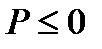В тех случаях, когда при вычислении того или иного предела непосредственный переход к пределу при 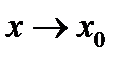приводит к одному из символов типа

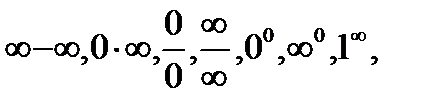
возникает ситуация, в которой становятся неприменимы теоремы об арифметических действиях над пределами. В таких случаях возникает неопределенность при решении вопроса о существовании предела или его величины. Эта неопределенность может быть снята после некоторых тождественных преобразований. В этом случае говорят, что тождественные преобразования приводят к раскрытию неопределенности. Поясним сказанное примером.

Пусть требуется вычислить предел 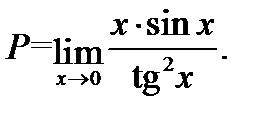Если в указанном отношении мы сразу же перейдем к пределу, то получим неопределенность типа 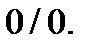Что скрывается под этим символом, мы пока не знаем. Попрубуем избавиться от неопределенности. Применим для этого таблицу 1 стандартных асимптотических разложений и теорему 5. Получим

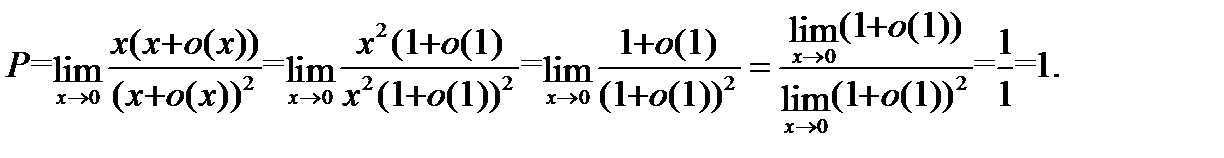
Лекция 2. Односторонние пределы функции в точке. Непрерывность функции. Разрывные функции и классификация точек разрыва. Производная функции, ее геометрический и физический смысл. Производная сложной функции. Таблица производных