Временное и стационарное уравнение Шредингера

Статистическое толкование волн де Бройля и соотношение неопределенностей Гейзенберга привели к выводу, что уравнением движения в квантовой механике, описывающим движение микрочастиц в различных силовых полях, должно быть уравнение, из которого бы вытекали наблюдаемые на опыте волновые свойства частиц. Основное уравнение должно быть уравнением относительно волновой функции 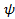(x,y,z,t), так как именно она, или точнее, величина 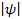², определяет вероятность пребывания частицы в момент времени t в объеме dV, т.е. в области с координатами х и х+dx, y и y+dy, z и z+dz. Так как искомое уравнение должно учитывать волновые свойства частиц, то оно должно быть волновым уравнением, подобно уравнению, описывающему электромагнитные волны.

Это уравнение постулируется, а его правильность подтверждается согласием с опытом получаемых с его помощью результатов.

Основное уравнение нерелятивистской квантовой механики (1926 г.)

4.1.Временное уравнение Шредингера:

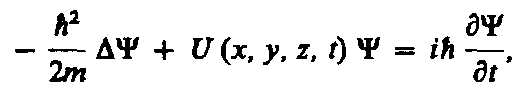
Уравнение справедливо для нерелятивистских частиц << ,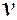

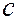где 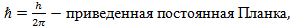{\displaystyle \hbar ={h \over 2\pi }} 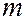– масса частицы; 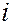- мнимая единица; 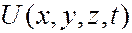– потенциальная функция частицы в силовом поле, в котором она движется; 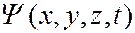– искомая волновая функция; ∆ – оператор Лапласа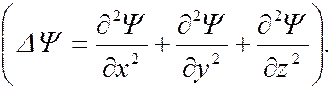

Условия, накладываемые на волновую функцию:

-Волновая функция должна быть конечной, однозначной и непрерывной.

-Производные ∂Ψ/∂x, ∂Ψ/∂y, ∂Ψ/∂z , ∂Ψ/∂t должны быть непрерывны.

-Функция 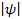² должна быть интегрируема (это условие сводится к условию нормировки вероятностей).

4.2.Стационарное уравнение Шредингера

В случае стационарного силового поля (функция U=U(x, у, z) не зависит явно от времени и имеет смысл потенциальной энергии. В данном случае решение уравнения Шредингера может быть представлено в виде произведения двух функций, одна из которых есть функция только координат, другая — только времени, причем зависимость от времени выражается множителем ).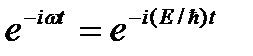

Тогда волновая функция для стационарных состояний (состояний с фиксированными значениями энергии) может быть представлена в виде:

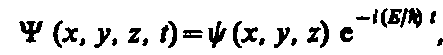
Стационарное уравнение Шредингера:

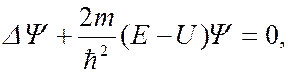
получилось после подстановки волновой функции во временное уравнение Шредингера и преобразований ( ∆ - оператор Лапласа, m – масса частицы; 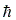- приведенная постоянная Планка ( 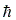= h/2π ); E – полная энергия частицы, U – потенциальная энергия частицы. В классической физике величина (E –U)равнялась бы кинетической энергии частицы. В квантовой механике вследствие соотношения неопределенностей понятие кинетической энергии лишено смысла. Здесь потенциальная энергия U – это характеристика внешнего силового поля, в котором движется частица. Это величина вполне определенная. Она также является функцией координат, в данном случае U=U(x,y,z)).

Собственные значения энергии

В уравнение Шредингера в качестве параметра входит полная энергия Е. Реальный физический смысл имеют только решения, которые выражаются только регулярными функциями 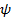( 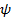должны быть конечными, однозначными и непрерывными вместе со своими первыми производными).

Регулярные решения имеют место лишь при определенном наборе Е, отвечающем данной задаче.

Эти значения энергии, удовлетворяющие уравнению Шредингера, называют собственными. Они могут образовать как непрерывный, так и дискретный спектр энергий.