Соотношение неопределенностей Гейзенберга

Во многих случаях классические представления (например, в каждый момент времени частица занимает в пространстве строго определенное место и обладает определенным импульсом) неприменимы для описания микрообъектов. Гейзенберг выдвинул идею о принципиальной невозможности измерения определенных пар связанных между собой характеристик так, чтобы они одновременно имели точные значения.

Соотношение неопределенностей для координат и импульсов:

Микрочастица (микрообъект) не может иметь одновременно точные значения координаты (x,y,z) и соответствующих компонентов импульса (p_x, p_y, p_z), причем произведение неопределенностей координаты и соответствующие ей проекции импульса не может быть меньше величины порядка .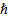

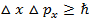
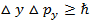
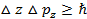
Физический смысл соотношения: Из соотношения неопределенностей следует, что если микрочастица находится, например, в состоянии с точным значением координаты 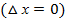, то в этом состоянии соответствующая проекция ее импульса оказывается совершенно неопределенной ( 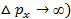, и наоборот. Таким образом, для микрочастицы не существует состояний, в которых ее координаты и импульс имели бы одновременно точные значения.

Соотношение неопределенностей для энергии и времени:

, (где r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">

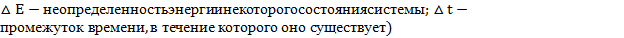
Физический смысл соотношения: из-за конечности времени жизни атомов в возбужденном состоянии энергия возбужденных состояний атомов не является точно определенной, потому частота излученного фотона также должна иметь неопределенность 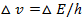. Тогда линии спектра должны иметь частоту v= . Опыт показывает, что все спектральные линии действительно размыты.

Невозможность одновременно точно определить координату и соответствующую проекцию импульса является следствием специфики микрообъектов, отражающей двойственность корпускулярно-волновой природы. Соотношение неопределенностей получено при одновременном использовании классических характеристик движения частицы (координаты, импульса) и наличия у них волновых свойств. Так как в классической механике принимается, что измерение координаты и импульса может быть произведено с любой точностью, то соотношение неопределенностей является, таким образом, квантовым ограничением применимости классической механики к микрообъектам.

Повышение точности в знании одной переменной, таким образом, ведет к понижению точности в знании другой и наоборот. Поэтому если в классической механике наличие координат и импульсов (скоростей) системы точно задает ее поведение во времени и в пространстве, то предсказание поведения квантовой системы должно носить вероятностный характер.