Бесконечно большие функции и их связь с
бесконечно малыми.
Определение. Предел функции f(x) при х®а, где а- число, равен бесконечности, если для любого числа М>0 существует такое число D>0, что неравенство
ïf(x)ï>M
выполняется при всех х, удовлетворяющих условию
0 < ïx - aï < D
Записывается 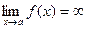 .
.
Собственно, если в приведенном выше определении заменить условие ïf(x)ï>M на f(x)>M, то получим:
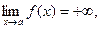
а если заменить на f(x)<M, то:
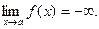
Графически приведенные выше случаи можно проиллюстрировать следующим образом:

a x a x a x
Определение. Функция называется бесконечно большойпри х®а, где а – чосли или одна из величин ¥, +¥ или -¥, если 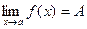 , где А – число или одна из величин ¥, +¥ или -¥.
, где А – число или одна из величин ¥, +¥ или -¥.
Связь бесконечно больших и бесконечно малых функций осуществляется в соответствии со следующей теоремой.
Теорема. Если f(x)®0 при х®а (если х®¥ ) и не обращается в ноль, то
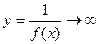
Сравнение бесконечно малых функций.
Пусть a(х), b(х) и g(х) – бесконечно малые функции при х ® а. Будем обозначать эти функции a, b и g соответственно. Эти бесконечно малые функции можно сравнивать по быстроте их убывания, т.е. по быстроте их стремления к нулю.
Например, функция f(x) = x10 стремится к нулю быстрее, чем функция f(x) = x.
Определение. Если 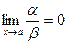 , то функция a называется бесконечно малой более высокого порядка, чем функция b.
, то функция a называется бесконечно малой более высокого порядка, чем функция b.
Определение. Если 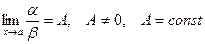 , то a и b называются бесконечно малыми одного порядка.
, то a и b называются бесконечно малыми одного порядка.
Определение. Если 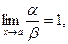 то функции a и b называются эквивалентными бесконечно малыми. Записывают a ~ b.
то функции a и b называются эквивалентными бесконечно малыми. Записывают a ~ b.
Пример. Сравним бесконечно малые при х®0 функции f(x) = x10 и f(x) = x.
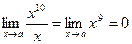
т.е. функция f(x) = x10 – бесконечно малая более высокого порядка, чем f(x) = x.
Определение. Бесконечно малая функция a называется бесконечно малой порядка kотносительно бесконечно малой функции b, если предел 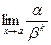 конечен и отличен от нуля.
конечен и отличен от нуля.
Однако следует отметить, что не все бесконечно малые функции можно сравнивать между собой. Например, если отношение 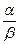 не имеет предела, то функции несравнимы.
не имеет предела, то функции несравнимы.
Пример. Если 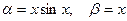 , то при х®0
, то при х®0 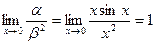 , т.е. функция a - бесконечно малая порядка 2 относительно функции b.
, т.е. функция a - бесконечно малая порядка 2 относительно функции b.
Пример. Если 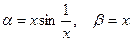 , то при х®0
, то при х®0 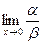 не существует, т.е. функция a и b несравнимы.
не существует, т.е. функция a и b несравнимы.
Некоторые замечательные пределы.
Первый замечательный предел. 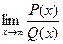 , где P(x) = a0xn + a1xn-1 +…+an,
, где P(x) = a0xn + a1xn-1 +…+an,
Q(x) = b0xm + b1xm-1 +…+bm - многочлены.
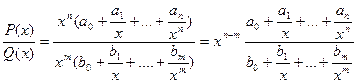
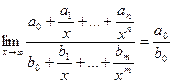

Итого: 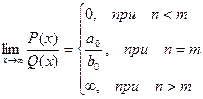

Второй замечательный предел. 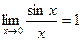

Третий замечательный предел. 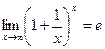
Часто если непосредственное нахождение предела какой – либо функции представляется сложным, то можно путем преобразования функции свести задачу к нахождению замечательных пределов.
Кроме трех, изложенных выше, пределов можно записать следующие полезные на практике соотношения:

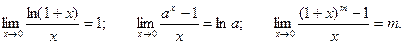
Непрерывность функции в точке.
Определение. Функция f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точкех0, если предел функции и ее значение в этой точке равны, т.е.
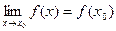
Тот же факт можно записать иначе: 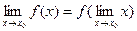
Определение. Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва.
Пример непрерывной функции:
 y
y
f(x0)+e
f(x0)
f(x0)-e
0 x0-D x0 x0+D x
 Пример разрывной функции:
Пример разрывной функции:
y
f(x0)+e
f(x0)
f(x0)-e
x0 x
Определение. Функция f(x) называется непрерывной в точке х0, если для любого положительного числа e>0 существует такое число D>0, что для любых х, удовлетворяющих условию
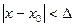
верно неравенство 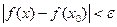 .
.
Определение. Функция f(x) называется непрерывной в точке х = х0, если приращение функции в точке х0 является бесконечно малой величиной.
f(x) = f(x0) + a(x)
где a(х) – бесконечно малая при х®х0.
Свойства непрерывных функций.
1) Сумма, разность и произведение непрерывных в точке х0 функций – есть функция, непрерывная в точке х0.
2) Частное двух непрерывных функций 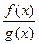 – есть непрерывная функция при условии, что g(x) не равна нулю в точке х0.
– есть непрерывная функция при условии, что g(x) не равна нулю в точке х0.
3) Суперпозиция непрерывных функций – есть непрерывная функция.
Это свойство может быть записано следующим образом:
Если u = f(x), v = g(x) – непрерывные функции в точке х = х0, то функция v = g(f(x)) – тоже непрерывнаяфункция в этой точке.
Справедливость приведенных выше свойств можно легко доказать, используя теоремы о пределах.
Непрерывность некоторых элементарных функций.
1) Функция f(x) = C, C = const – непрерывная функция на всей области определения.
2) Рациональная функция 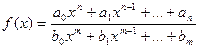 непрерывна для всех значений х, кроме тех, при которых знаменатель обращается в ноль. Таким образом, функция этого вида непрерывна на всей области определения.
непрерывна для всех значений х, кроме тех, при которых знаменатель обращается в ноль. Таким образом, функция этого вида непрерывна на всей области определения.
3) Тригонометрические функции непрерывны на своей области определения.
Точки разрыва и их классификация.
Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х0, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х0 является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.
Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.
Если односторонний предел (см. выше) 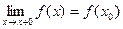 , то функция называется непрерывной справа.
, то функция называется непрерывной справа.

х0
Если односторонний предел (см. выше) 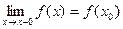 , то функция называется непрерывной слева.
, то функция называется непрерывной слева.

х0
Определение. Точка х0 называется точкой разрывафункции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке.
Определение. Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.
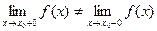
Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х0, достаточно того, что она определена слева и справа от нее.
Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимойточкой разрыва, но подробнее об этом поговорим ниже.
Определение. Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
Непрерывность функции на интервале и на отрезке.
Определение. Функция f(x) называется непрерывной на интервале (отрезке), если она непрерывна в любой точке интервала (отрезка).
Комплексные числа.
Определение. Комплексным числом zназывается выражение 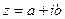 , где a и b – действительные числа, i – мнимая единица, которая определяется соотношением:
, где a и b – действительные числа, i – мнимая единица, которая определяется соотношением:

При этом число a называется действительной частью числа z (a = Re z), а b- мнимой частью (b = Im z).
Если a =Re z =0, то число z будет чисто мнимым, если b = Im z = 0, то число z будет действительным.
Определение. Числа 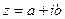 и
и 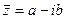 называются комплексно – сопряженными.
называются комплексно – сопряженными.
Определение. Два комплексных числа 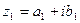 и
и 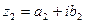 называются равными, если соответственно равны их действительные и мнимые части:
называются равными, если соответственно равны их действительные и мнимые части:

Определение. Комплексное число равно нулю, если соответственно равны нулю действительная и мнимая части.
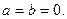
Понятие комплексного числа имеет геометрическое истолкование. Множество комплексных чисел является расширением множества действительных чисел за счет включения множества мнимых чисел. Комплексные числа включают в себя все множества чисел, которые изучались ранее. Так натуральные, целые, рациональные, иррациональные, действительные числа являются, вообще говоря, частными случаями комплексных чисел.
Если любое действительное число может быть геометрически представлено в виде точки на числовой прямой, то комплексное число представляется точкой на плоскости, координатами которой будут соответственно действительная и мнимая части комплексного числа. При этом горизонтальная ось будет являться действительной числовой осью, а вертикальная - мнимой осью.

у
A(a, b)
r b
j
0 a x
Таким образом, на оси ОХ располагаются действительные числа, а на оси ОY – чисто мнимые.
С помощью подобного геометрического представления можно представлять числа в так называемой тригонометрической форме.
Тригонометрическая форма числа.
Из геометрических соображений видно, что 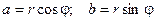 . Тогда комплексное число можно представить в виде:
. Тогда комплексное число можно представить в виде:

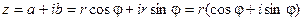
Такая форма записи называется тригонометрической формой записи комплексного числа.
При этом величина r называется модулемкомплексного числа, а угол наклона j -аргументомкомплексного числа.
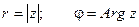 .
.
Из геометрических соображений видно:

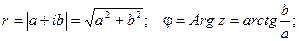
Очевидно, что комплексно – сопряженные числа имеют одинаковые модули и противоположные аргументы.
Действия с комплексными числами.
Основные действия с комплексными числами вытекают из действий с многочленами.
1) Сложение и вычитание.

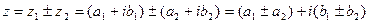
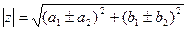
2) Умножение.
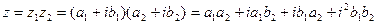

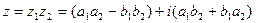
В тригонометрической форме:
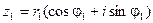 ,
, 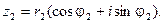

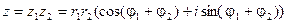
С случае комплексно – сопряженных чисел:
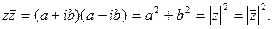
3) Деление.
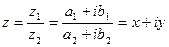
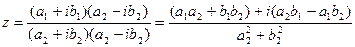

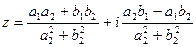
 В тригонометрической форме:
В тригонометрической форме:
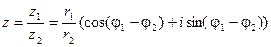
4) Возведение в степень.
Из операции умножения комплексных чисел следует, что
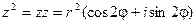
В общем случае получим:

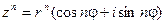 ,
,
где n – целое положительное число.
Это выражение называется формулой Муавра.
(Абрахам де Муавр (1667 – 1754) – английский математик)
Формулу Муавра можно использовать для нахождения тригонометрических функций двойного, тройного и т.д. углов.
5) Извлечение корня из комплексного числа.
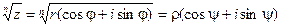
Возводя в степень, получим:
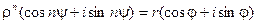
Отсюда: 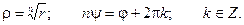

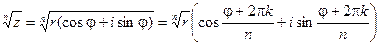
Таким образом, корень n – ой степени из комплексного числа имеет n различных значений.
Показательная форма комплексного числа.
Рассмотрим показательную функцию 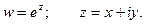
Можно показать, что функция w может быть записана в виде:

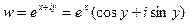
Данное равенство называется уравнением Эйлера.Вывод этого уравнения будет рассмотрен позднее. (См. ).
Для комплексных чисел будут справедливы следующие свойства:
1) 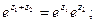
2) 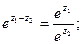
3) 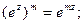 где m – целое число.
где m – целое число.
Если в уравнении Эйлера показатель степени принять за чисто мнимое число (х=0), то получаем:
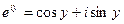
Для комплексно – сопряженного числа получаем:
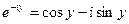
Из этих двух уравнений получаем:

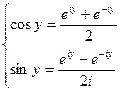
Этими формулами пользуются для нахождения значений степеней тригонометрических функций через функции кратных углов.
Если представить комплексное число в тригонометрической форме:
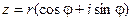
и воспользуемся формулой Эйлера: 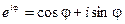

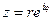
Полученное равенство и есть показательная форма комплексного числа.
Разложение многочлена на множители.
Определение. Функция вида f(x) 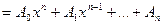 называется целой рациональной функцией от х.
называется целой рациональной функцией от х.
Теорема Безу. (Этьенн Безу (1730 – 1783) – французский математик)
При делении многочлена f(x) на разность x – a получается остаток, равный f(a).
Определение. Если уравнение имеет вид Р(х) = 0, где Р(х) – многочлен степени n, то это уравнение называется алгебраическим уравнением степени n.
Теорема. (Основная теорема алгебры) Всякая целая рациональная функция f(x) имеет, по крайней мере, один корень, действительный или комплексный.
Теорема. Всякий многочлен n – ой степени разлагается на n линейных множителей вида (x – a) и множитель, равный коэффициенту при xn.
Теорема. Если два многочлена тождественно равны друг другу, то коэффициенты одного многочлена равны соответствующим коэффициентам другого.
Элементы высшей алгебры.
Основные понятия теории множеств.
Определение. Множеством Мназывается объединение в единое целое определенных различимых объектов а, которые называются элементамимножества.
а Î М
Множество можно описать, указав какое – нибудь свойство, присущее всем элементам этого множества.
Множество, не содержащее элементов, называется пустыми обзначается Æ.
Определение. Если все элементы множества А являются также элементами множества В, то говорят, что множество А включается (содержится) в множестве В.


А
В
А Ì В
Определение. Если А Í В, то множество А называется подмножествоммножества В, а если при этом А ¹ В, то множество А называется собственным подмножеством множества В и обозначается А Ì В.
Для трех множеств А, В, С справедливы следующие соотношения.
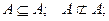
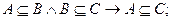
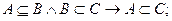
Связь между включением и равенством множеств устанавливается следующим соотношением:
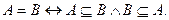
Здесь знак Ù обозначает конъюнкцию(логическое “и”).
Операции над множествами.
Определение. Объединениеммножеств А и В называется множество С, элементы которого принадлежат хотя бы одномк из множеств А и В.
Обозначается С = А È В.

А
В
Геометрическое изображение множеств в виде области на плоскости называется диаграммой Эйлера – Венна.
Определение. Пересечениеммножеств А и В называется множество С, элементы которого принадлежат каждому из множеств А и В.
Обозначение С = А Ç В.

А С В
Для множеств А, В и С справедливы следующие свойства:
А Ç А = А È А = А; A È B = B È A; A Ç B = B Ç A;
(A Ç B) Ç C = A Ç (B Ç C); (A È B) È C = A È (B È C);
A È (B Ç C) = (A È B) Ç (A È C); A Ç (B È C) = (A Ç B) È (A Ç C);
A È (A Ç B) = A; A Ç (A È B) = A;
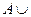 Æ = А; A Ç Æ = Æ;
Æ = А; A Ç Æ = Æ;
Определение. Разностьюмножеств А и В называется множество, состоящее из элементов множества А, не принадлежащих множеству В.
Обозначается С = А \ В.

А В
Определение. Симметрической разностью множеств А и В называется множество С, элементы которого принадлежат в точности одному из множеств А или В.
Обозначается А D В.
А D В = (A \ B) È (B \ A)

A B
Определение. СЕ называется дополнениеммножества А относительно множества Е, если А Í Е и CЕ = Е \ A.

A E
Отношения и функции.
Определение. Упорядоченной парой (a, b) двух элементов a и b называется множество {{a},{a, b}}.
Для любых элементов a, b, c, d справедливо соотношение:
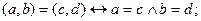
Определение. Декартовым произведениеммножеств А и В называется множество всех упорядоченных пар (a, b), где аÎА, bÎB.

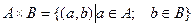
Декартово произведение п равных множеств А будет называться п – й декартовой степенью множества А и обозначаться Аn.
Определение. n – мерным отношениемR на непустом множестве А называется подмножество Аn. Если R – n – мерное отношение на множестве А и (а1,а2,…аn)ÎR, то говорят, что отношение R выполняется для элементов а1,а2,…аn и записывают R а1а2…аn. Если n = 2, то такое отношение называется бинарным.
Для бинарного отношения вместо общей записи Ra1a2 применяют запись а1Ra2.
Свойства бинарных отношений.
Определение. Произведением двух бинарных отношений R и S, заданных на множестве А, называется множество
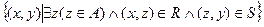
Знак | называется штрих Шеффера и обозначает антиконъюнкцию.
Определение. Обратным (инверсным) отношением к отношению R, заданному на множестве А, называется отношение R-1, определяемое равенством:
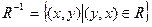
Дискретная математика.
Элементы математической логики.
Математическая логика – разновидность формаьной логики, т.е. науки, которая изучает умозаключения с точки зрения их формального строения.
Определение. Высказыванием называется предложение, к которому возможно применить понятия истинно или ложно.
В математической логике не рассматривается сам смысл высказываний, определяется только его истинность или ложность, что принято обозначать соответственно И или Л.
Понятно, что истинные и ложные высказывания образуют соответствующие множества. С помощью простых высказываний можно составлять более сложные, соединяя простые высказывания союзами “и”, “или”.
Таким образом, операции с высказываниями можно описывать с помощью некоторого математического аппарата.
Вводятся следующие логические операции (связки) над высказываниями
1) Отрицание. Отрицанием высказывания Р называется высказывание, которое истинно только тогда, когда высказывание Р ложно.
Обозначается 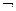 Р или
Р или 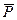 .
.
Соответствие между высказываниями определяется таблицами истинности. В нашем случае эта таблица имеет вид:
| P | 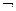 Р Р
|
| И | Л |
| Л | И |
2) Конъюнкция. Конъюнкцией двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинны оба высказывания.
Обозначается P&Q или РÙQ.
| P | Q | P&Q |
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | Л |
3) Дизъюнкция. Дизъюнкцией двух высказываний P и Q называется высказывание, ложное тогда и только тогда, когда оба высказывания ложны.
Обозначается PÚQ.
| P | Q | PÚQ |
| И | И | И |
| И | Л | И |
| Л | И | И |
| Л | Л | Л |
4) Импликация. Импликацией двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда высказывание Р истинно, а Q – ложно.
Обозначается PÉQ (или РÞQ). Высказывание Р называется посылкой импликации, а высказывание Q – следствием.
| P | Q | PÞQ |
| И | И | И |
| И | Л | Л |
| Л | И | И |
| Л | Л | И |
5) Эквиваленция. Эквиваленцией двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинности высказываний совпадают.
Обозначается Р~Q или РÛQ.
| P | Q | P~Q |
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | И |
С помощью этих основных таблиц истинности можно составлять таблицы истинности сложных формул.
Основные равносильности.
Для любых формул А, В и С справедливы следующие равносильности:
A & B º B & A; A & A º A; A & (B & C) º (A & B) & C;
A Ú B º B Ú A; A Ú A º A; A Ú (B Ú C) º (A Ú B) Ú C;
A Ú (B & C) º (A Ú B) & (A Ú C); A & (B Ú C) º (A & B) Ú (A & C);
A & (A Ú B) º A; A Ú (A & B) º A; ØØA º A; Ø(A & B) º ØA Ú ØB;
A º (A & B) Ú (A & ØB); A º (A Ú B) & (A Ú ØB);
Булевы функции.
Определение. Булевой функциейf(X1, X2, …, Xn) называется называется произвольная n – местная функция, аргументы и значения которой принадлежат множеству {0, 1}.
Вообще говоря между логическими высказываниями, логическими связками и булевыми функциями просматривается явная аналогия. Если логические функции могут принимать значения истинно или ложно, то для булевой функции аналогами этих значений будут значения 0 или 1.
Для булевых функций также можно составить таблицы значений, соответствующим основным логическим операциям.
| X1 | X2 | ØX1 | X1&X2 | X1ÚX2 | X1ÞX2 | X1ÛX2 |
Исчисление предикатов.
Определение. ПредикатомP(x1, x2, …, xn) называется функция, переменные которой принимают значения из некоторого множества М, а сама функция принимает два значения: И (истина) и Л (ложь), т.е.
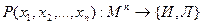
Предикат от п аргументов называется п – местным предикатом. Высказывания считаются нуль – местными предикатами.
Над предикатами можно производить обычные логические операции, в результате которых получаются новые предикаты.
Кроме обычных логических операций к предикатам применяются также специальные операции, называемые кванторами.
Кванторы бывают двух видов:
1) Квантор общности. Обозначается ("х)Р(х). Квантором общности называется высказывание истинное, когда Р(х) истинно для каждого элемента х из множества М, и ложное – в противном случае.
2) Квантор существования. Обозначается ($х)Р(х). Квантором существования называется высказывание, истинное, когда существует элемент из множества М, для которого Р(х) истинно, и ложное в противном случае.
Операцию связывания квантором можно применять и к предикатам от большего числа переменных.
Для формул логики предикатов сохраняется справедливость всех правил равносильных преобразований логики высказываний. Кроме того, справедливы следующие свойства:
1) Перенос квантора через отрицание.
Ø("x)A(x) º ($x)ØA(x); Ø($x)A(x) º ("x)ØA(x);
2) Вынесение квантора за скобки.
($х)(А(х) & B) º ($x)A(x) & B; ("x)(A(x) & B) º ("x)A(x) & B;
($х)(А(х) Ú B) º ($x)A(x) Ú B; ("x)(A(x) Ú B) º ("x)A(x) Ú B;
3) Перестановка одноименных кванторов.
("y)("x)A(x,y) º ("x)("y)A(x,y); ($y)($x)A(x,y) º ($x)($y)A(x,y);
4) Переименование связанных переменных. Если заменить связанную переменную формулы А другой переменной, не входящей в эту формулу, в кванторе и всюду в области действия квантора получаем формулу, равносильную А.
Исчисление предикатов базируется на приведенных выше свойствах и правилах, называемых аксиомами.
Какими бы ни были формулы А и В для них справедливы следующие аксиомы:
1) A Þ (B Þ A);
2) (A Þ (B Þ C)) Þ ((A Þ B) Þ (A Þ C));
3) (ØB Þ ØA) Þ ((ØB Þ A) Þ B);
4) ("xi)A(xi) Þ A(xj), где формула А(хi) не содержит переменной xi.
5) A(xi) Þ ($xj)A(xj), где формула А(хi) не содержит переменной xi.
Конечные графы и сети.
Основные определения.
Определение. Если на плоскости задать конечное множество V точек и конечный набор линий Х, соединяющих некоторые пары из точек V, то полученная совокупность точек и линий будет называться графом.
При этом элементы множества V называются вершинами графа, а элементы множества Х – ребрами.
В множестве V могут встречаться одинаковые элементы, ребра, соединяющие одинаковые элементы называются петлями. Одинаковые пары в множестве Х называются кратными (или параллельными) ребрами. Количество одинаковых пар
(v, w) в Х называется кратностьюребра (v, w).
Множество V и набор Х определяют граф с кратными ребрами – псевдограф.
G = (V, X)
Псевдограф без петель называется мультиграфом.
Если в наборе Х ни одна пара не встречается более одного раза, то мультиграф называется графом.
Если пары в наборе Х являются упорядочными, то граф называется ориентированным или орграфом.
Графу соответствует геометрическая конфигурация. Вершины обозначаются точками (кружочками), а ребра – линиями, соединяющими соответствующие вершины.
Определение. Если х = {v, w} – ребро графа, то вершины v, w называются концами ребра х.
Если х = (v, w) – дуга орграфа, то вершина v – начало, а вершина w – конец дуги х.
Определение. Вершины v, w графа G = (V, X) называются смежными, если {v,w}ÎX. Два ребра называются смежными, если они имеют общюю вершину.
Определение. Степенью вершины графа называется число ребер, которым эта вершина принадлежит. Вершина называется изолированной, если если ее степень равна единице и висячей, если ее степень равна нулю.
Определение.Графы G1(V1, X1) и G2(V2, X2) называются изоморфмными, если существует взаимно однозначное отображение j: V1 ® V2, сохраняющее смежность.
Определение. Маршрутом (путем) для графа G(V, X) называется последовательность v1x1v2x2v3…xkvk+1. Маршрут называется замкнутым, если его начальная и конечная точки совпадают. Число ребер (дуг) маршрута (пути) графа называется длиноймаршрута (пути).
Определение. Незамкнутый маршрут (путь) называется цепью. Цепь, в которой все вершины попарно различны, называется простой цепью.
Определение. Замкнутый маршрут (путь) называется циклом (контуром). Цикл, в котором все вершины попарно различны, называется простым циклом.
Матрицы графов.
Пусть D = (V, X) – орграф, где V = {v1, …, vn}, X = {x1, … , xm}.
Определение. Матрицей смежности орграфа D называется квадратичная матрица A(D) = [aij] порядка п, у которой
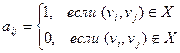
Определение. Если вершина v является крнцом ребра х, то говорят, что v и х –инциндентны.
Определение. Матрицей инциндентности оргафа D называется матрица размерности п´т B(D) = [bij], у которой
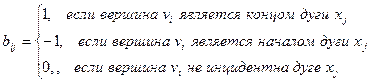
Пример. Записать матрицы смежности и инцидентности для графа, изображенного на рисунке.
x1

v1 x4 v2
x2
x3
v3
Составим матрицу смежности:
| v1 | v2 | v3 | |
| v1 | |||
| v2 | |||
| v3 |
Т.е. 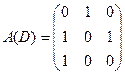 - матрица смежности.
- матрица смежности.
Матрица инциндентности:
| x1 | x2 | x3 | x4 | |
| v1 | -1 | |||
| v2 | -1 | -1 | ||
| v3 | -1 |
Т.е. 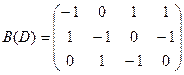
Если граф имеет кратные дуги (ребра), то в матрице смежности принимается aij=k, где k – кратность дуги (ребра).
Достижимость и связность.
Определение. Вершина w графа D (или орграфа) называется достижимой из вершины v, если либо w=v, либо существует путь из v в w(маршрут, соединяющий v и w).
Определение. Граф (орграф) называется связным, если для любых двух его вершин существует маршрут (путь), который их связывает. Орграф называется односторонне связным, если если для любых двух его вершин по крайней мере одна достижима из другой.
Определение. Псевдографом D(V, X), ассоциированным с ориентированным псевдографом, называется псевдограф G(V, X0) в котором Х0 получается из Х заменой всех упорядоченных пар (v, w) на неупорядоченные пары (v, w).
Определение.Орграф называется слабо связным, если связным является ассоциированный с ним псевдограф.
Эйлеровы и гамильтоновы графы.
Определение. Цепь (цикл) в псевдографе G называется эйлеровым, если она проходит по одному разу через каждое ребро псевдографа G.
Теорема. Для того, чтобы связный псевдограф G обладал эйлеровым циклом, необходимо и достаточно, чтобы степени его вершин были четными.
Теорема.<
Дата добавления: 2017-10-04; просмотров: 1592;











