Конические поверхности второго порядка. Конические сечения

О п р е д е л е н и е. Поверхность, образованная прямыми, проходящими через данную точку и пересекающими данную линию или имеющими относительно этой линии асимптотическое направление, называется конической поверхностью.

Если в качестве направляющей конической поверхности выбрать пару пересекающихся, пару совпавших или пару параллельных прямых и вершину, не принадлежащую плоскости этих прямых, то коническая поверхность будет представлять собой пару пересекающихся или совпавших плоскостей – вырожденные конусы.

У п р а ж н е н и е. Пусть в пространстве задана прямоугольная система координат 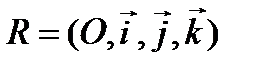. В плоскости, параллельной 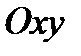задан эллипс .

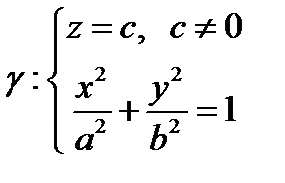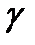Покажите, что уравнение конической поверхности с вершиной и направляющей будет иметь вид 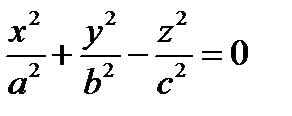– уравнение невырожденного конуса.

Рассматривая сечения невырожденного конуса различными плоскостями, не проходящими через его вершину, можно получить

· эллипс, если плоскость пересекает все образующие конуса;

· гиперболу, если плоскость параллельна двум образующим конуса;

· параболу, если плоскость параллельна только одной образующей конуса.

Эллипс, гипербола, парабола называются коническими сечениями.

Отметим, что любое однородное уравнение второй степени определяет в пространстве коническую поверхность.