Расстояние от точки до плоскости

Для плоскости 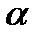, заданной уравнением 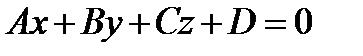относительно прямоугольной системы координат 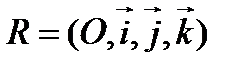, вектор

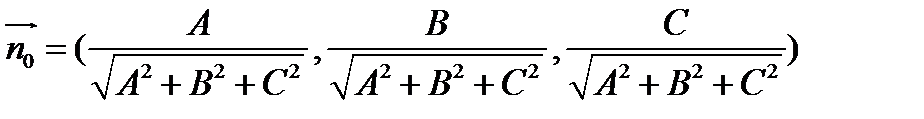
является ортом вектора .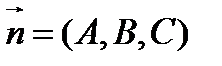

Для точки 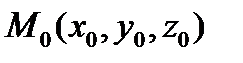пространства существует точка 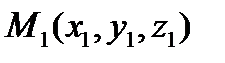в плоскости 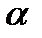, такая, что .

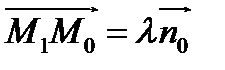Расстояние от точки 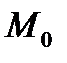до плоскости 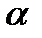равно длине вектора 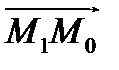, а значит модулю числа .

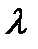Имеем .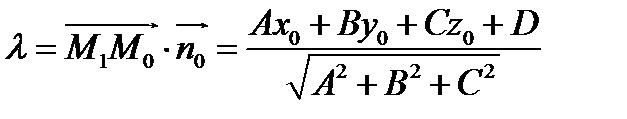

Получаем формулу вычисления расстояния от точки до плоскости

.

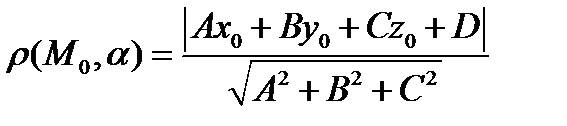Лекция 2. Прямая в пространстве

Уравнение прямой в пространстве

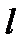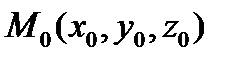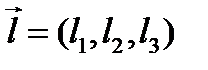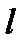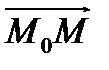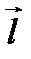Прямая в пространстве однозначно определяется точкой и направляющим вектором . Произвольная точка пространства принадлежит прямой тогда и только тогда, когда векторы и коллинеарны, то есть отличаются друг от друга числовым множителем 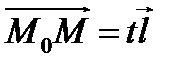, их координаты пропорциональны. Имеем

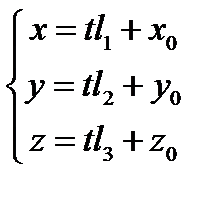– параметрические уравнения прямой,

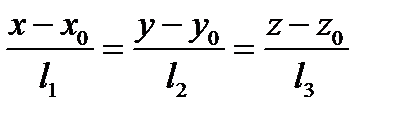– каноническое уравнение прямой.

Прямая может быть задана как пересечение двух плоскостей, то есть системой двух линейных уравнений

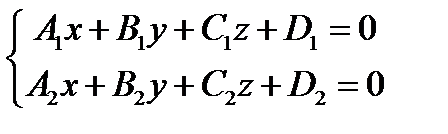– общие уравнения прямой.

Несложно проверить, что вектор

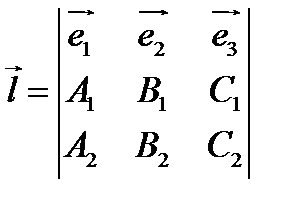
параллелен плоскостям, определяющим прямую, а значит, является направляющим вектором этой прямой.