Цилиндрические поверхности

О п р е д е л е н и е. Пусть в пространстве даны линия 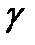и прямая 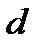. Поверхность, образованная прямыми, параллельными 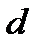и пересекающими 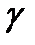, называется цилиндрической поверхностью.

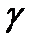– направляющая, прямые – образующие цилиндрической поверхности.

Т е о р е м а. Пусть в пространстве задана прямоугольная система координат 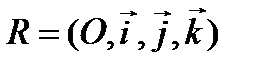и в плоскости 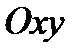в системе координат 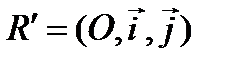задана линия 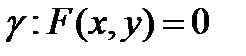. Тогда уравнение 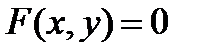определяет в пространстве цилиндрическую поверхность с направляющей 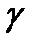и образующими, параллельными оси .

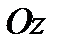Если уравнение 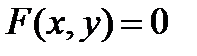- уравнение второй степени, то цилиндрическая поверхность с направляющей 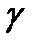и образующими, параллельными оси 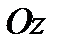является цилиндрической поверхностью второго порядка.

В зависимости от того, к какому сорту линий второго порядка относится направляющая, будем иметь:

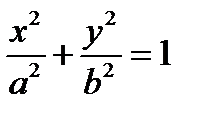– эллиптический цилиндр;

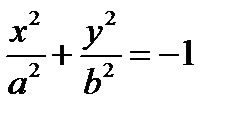– мнимый эллиптический цилиндр;

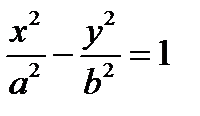– гиперболический цилиндр;

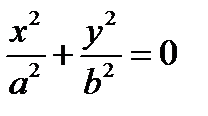– пара мнимых пересекающихся плоскостей;

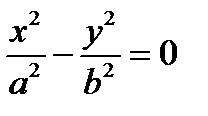– пара пересекающихся плоскостей;

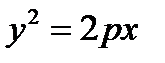– параболический цилиндр;

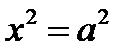– пара параллельных плоскостей;

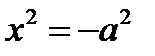– пара мнимых пересекающихся плоскостей;

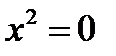– пара совпавших плоскостей.