Прямолинейные образующие поверхностей второго порядка

Прямая 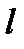называется прямолинейной образующей поверхности Ф, если каждая точка этой прямой принадлежит поверхности Ф.

1. Образующие цилиндрической и конической поверхностей являются их прямолинейными образующими.

2. Так как все точки эллипсоида находятся внутри параллелепипеда, то эллипсоид не имеет прямолинейных образующих.

3. Покажите, что двуполостный гиперболоид и эллиптический параболоид не имеют прямолинейных образующих.

4. Представив уравнение 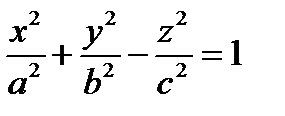однополостного гиперболоида в виде

,

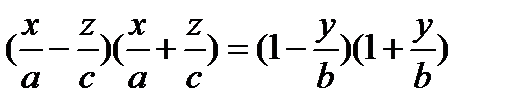замечаем, что для каждого действительного числа 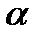каждая из прямых, определяемых уравнениями

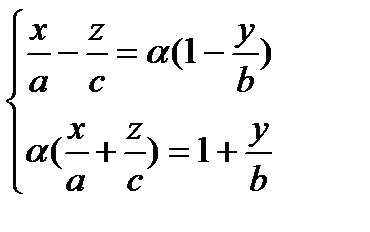и ,

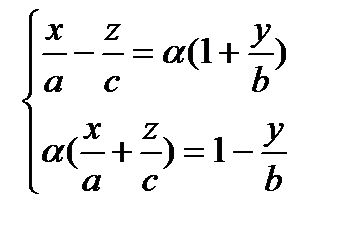целиком лежит на однополостном гиперболоиде, а значит, является прямолинейной образующей.

Таким образом, на однополостном гиперболоиде имеем два семейства прямолинейных образующих, обладающие свойствами:

a. Через каждую точку поверхности проходит в точности по одной прямолинейной образующей из каждого семейства.

b. Две прямолинейные образующие одного семейства скрещиваются.

c. Две прямолинейные образующие разных семейств лежат в одной плоскости.

5. Аналогично можно показать, что на гиперболическом параболоиде существуют два семейства прямолинейных образующих, обладающие свойствами a-c и свойством

d. Все прямолинейные образующие одного семейства параллельны одной плоскости.