Уравнение плоскости
Через данную точку 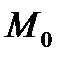 проходит единственная плоскость
проходит единственная плоскость 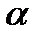 , параллельная двум данным неколлинеарным векторам
, параллельная двум данным неколлинеарным векторам 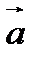 и
и 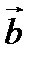 .
.
Пусть в пространстве задан аффинный репер 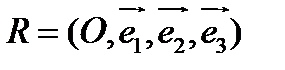 и
и 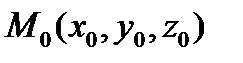 ,
, 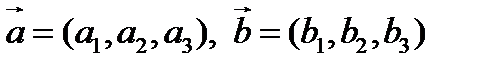 . Точка
. Точка 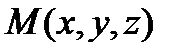 принадлежит плоскости
принадлежит плоскости 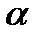 тогда и только тогда, когда векторы
тогда и только тогда, когда векторы 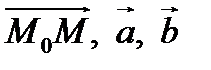 компланарны, то есть вектор
компланарны, то есть вектор 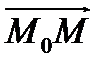 можно выразить через векторы
можно выразить через векторы 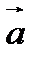 и
и 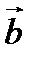 :
:
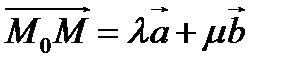 .
.
Переходя к координатам, найдем уравнения, которым должны удовлетворять координаты 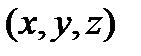 точки, принадлежащей плоскости:
точки, принадлежащей плоскости:
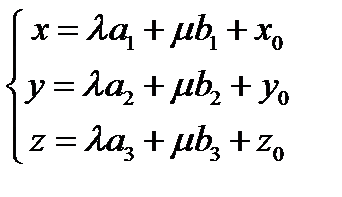 – параметрические уравнения плоскости.
– параметрические уравнения плоскости.
Условием компланарности векторов 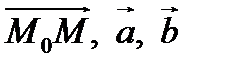 является равенство нулю определителя, составленного из координат этих векторов:
является равенство нулю определителя, составленного из координат этих векторов:
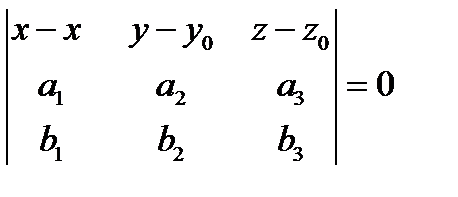 – общее уравнение плоскости.
– общее уравнение плоскости.
Общее уравнение плоскости приводится к виду
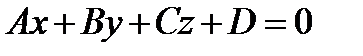 , где
, где 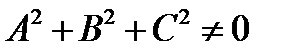 .
.
Пусть плоскость 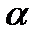 пересекает все три оси координат в точках
пересекает все три оси координат в точках 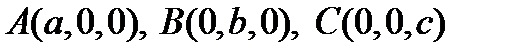 . Имеем два неколлинеарных вектора
. Имеем два неколлинеарных вектора 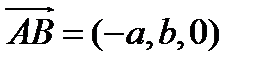 и
и 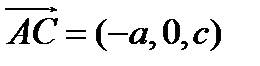 , параллельных плоскости
, параллельных плоскости 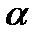 . Тогда получаем уравнение плоскости
. Тогда получаем уравнение плоскости
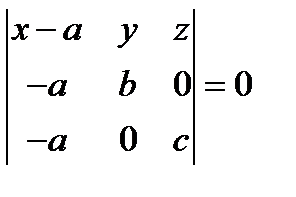 или
или 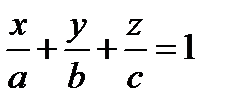 – уравнение плоскости в отрезках.
– уравнение плоскости в отрезках.
Через данную точку 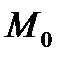 проходит единственная плоскость
проходит единственная плоскость 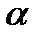 , перпендикулярная данному ненулевому вектору
, перпендикулярная данному ненулевому вектору 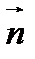 . Вектор
. Вектор 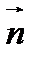 , как и любой другой ненулевой вектор, перпендикулярный плоскости
, как и любой другой ненулевой вектор, перпендикулярный плоскости 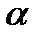 , называется нормальным вектором плоскости.
, называется нормальным вектором плоскости.
Точка 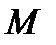 принадлежит плоскости
принадлежит плоскости 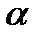 тогда и только тогда, когда векторы
тогда и только тогда, когда векторы 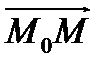 и
и 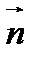 ортогональны, то есть их скалярное произведение равно нулю. Чтобы выразить условие ортогональности векторов через координаты, необходим ортонормированный базис, а значит, в пространстве должна быть задана прямоугольная система координат
ортогональны, то есть их скалярное произведение равно нулю. Чтобы выразить условие ортогональности векторов через координаты, необходим ортонормированный базис, а значит, в пространстве должна быть задана прямоугольная система координат 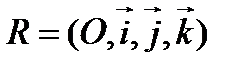 . Пусть
. Пусть 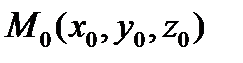 ,
, 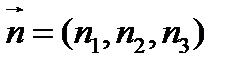 . Выразив условие ортогональности векторов
. Выразив условие ортогональности векторов 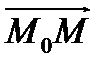 и
и 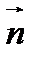 через координаты, получим уравнение плоскости
через координаты, получим уравнение плоскости 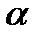 :
: 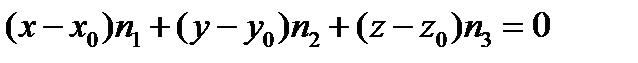 .
.
Выводы:
1. Чтобы составить уравнение плоскости, надо знать точку и два неколлинеарных вектора, параллельных этой плоскости, либо точку и нормальный вектор.
2. Уравнение плоскости приводится к виду
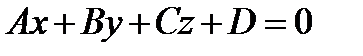 , где
, где 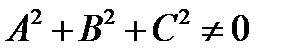 ,
,
то есть плоскость является алгебраической поверхностью первого порядка.
Т е о р е м а. Любая алгебраическая поверхность первого порядка является плоскостью.
Д о к а з а т е л ь с т в о. Для алгебраической поверхности первого порядка существует аффинная система координат, относительно которой поверхность задается уравнением 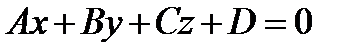 , где
, где 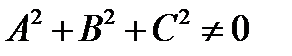 .
.
Пусть 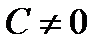 . Приведя уравнение поверхности к виду
. Приведя уравнение поверхности к виду 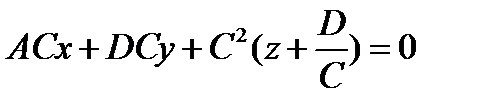 , получим равносильное уравнение
, получим равносильное уравнение
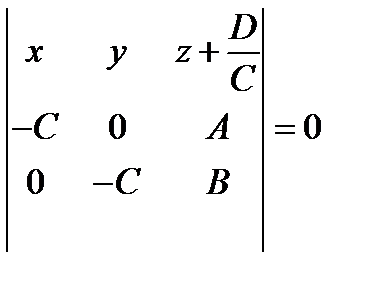 .
.
Это есть уравнение плоскости, проходящей через точку 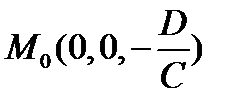 параллельно векторам
параллельно векторам 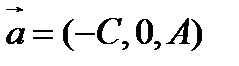 и
и 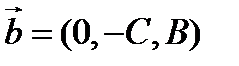 .
.
Дата добавления: 2021-09-25; просмотров: 529;











