Сжатие пространства к плоскости

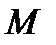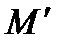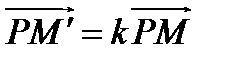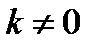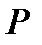О п р е д е л е н и е. Отображение пространства в себя, при котором каждой точке соответствует точка такая, что , где , – ортогональная проекция точки 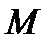на данную плоскость 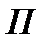, называется сжатием пространства к плоскости 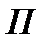с коэффициентом .

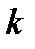Несложно найти формулы сжатия к плоскости : .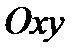

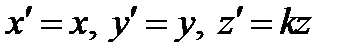Эллипсоид

О п р е д е л е н и е. Поверхность, полученная вращением эллипса вокруг его оси симметрии, называется эллипсоидом вращения.

Пусть в пространстве задана прямоугольная система координат 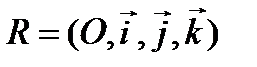и в плоскости 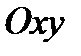в репере 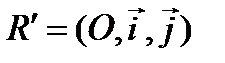эллипс задан каноническим уравнением . Чтобы получить эллипсоид вращения с осью 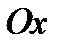, достаточно рассмотреть линию, заданную уравнением .

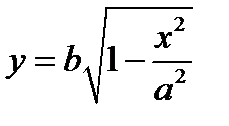Поверхность, полученная при вращении этой линии вокруг оси 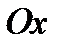, будет задаваться уравнением .

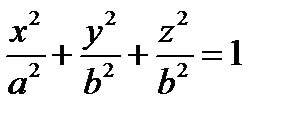О п р е д е л е н и е. Поверхность, полученная из эллипсоида вращения путем сжатия к плоскости, проходящей через ось вращения, называется эллипсоидом.

Чтобы найти уравнение эллипсоида, нужно в уравнение эллипсоида вращения вместо координат точки ( 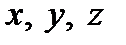) подставить их выражения через координаты 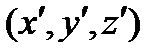образа этой точки при сжатии к плоскости . Получим каноническое уравнение эллипсоида: .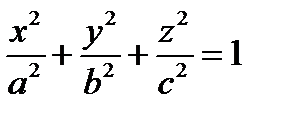

Самостоятельно исследовать методом сечений и построить эллипсоид.

Гиперболоиды

О п р е д е л е н и е. Поверхность, полученная вращением гиперболы вокруг её мнимой оси, называется однополостным гиперболоидом вращения.

Пусть в пространстве задана прямоугольная система координат 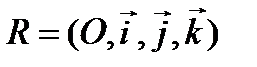и в плоскости 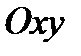в репере 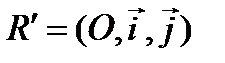гипербола задана каноническим уравнением 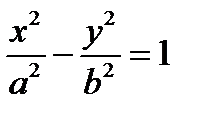. Чтобы получить однополостный гиперболоид вращения, достаточно рассмотреть одну ветвь гиперболы, заданную уравнением .

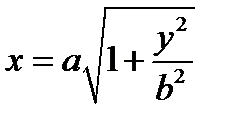Поверхность, полученная при вращении этой линии вокруг оси 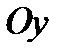, будет задаваться уравнением 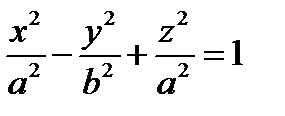– каноническое уравнение однополостного гиперболоида вращения.

О п р е д е л е н и е. Поверхность, полученная из однополостного гиперболоида вращения путем сжатия к плоскости, проходящей через ось вращения, называется однополостным гиперболоидом.

Выполнив сжатие к плоскости 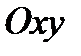, получим каноническое уравнение однополостного гиперболоида:

.

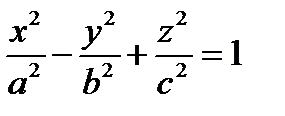Самостоятельно исследовать методом сечений и построить однополостный гиперболоид.

О п р е д е л е н и е. Поверхность, полученная вращением гиперболы вокруг её действительной оси, называется двуполостным гиперболоидом вращения.

Пусть в пространстве задана прямоугольная система координат 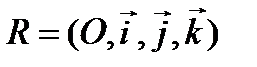и в плоскости 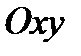в репере 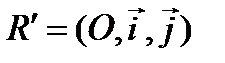гипербола задана каноническим уравнением 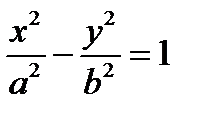. Чтобы получить двуполостный гиперболоид вращения, достаточно рассмотреть точки гиперболы, расположенные в полуплоскости 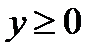. Это будут точки, задаваемые уравнением: .

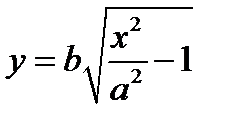Поверхность, полученная при вращении этой линии вокруг оси , будет задаваться уравнением 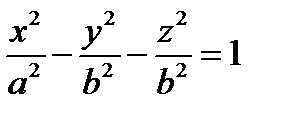– каноническое уравнение двуполостного гиперболоида вращения.

О п р е д е л е н и е. Поверхность, полученная из двуполостного гиперболоида вращения путем сжатия к плоскости, проходящей через ось вращения, называется двуполостным гиперболоидом.

Выполнив сжатие к плоскости , получим каноническое уравнение двуполостного гиперболоида:

.

Самостоятельно исследовать методом сечений и построить двуполостный гиперболоид.

Параболоиды

О п р е д е л е н и е. Поверхность, полученная вращением параболы вокруг её оси, называется параболоидом вращения.

Пусть в пространстве задана прямоугольная система координат 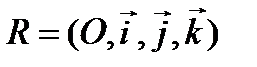и в плоскости 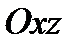в репере 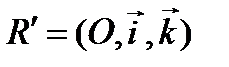парабола задана каноническим уравнением 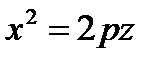. Чтобы получить параболоид вращения, достаточно рассмотреть одну ветвь параболы, заданную уравнением .

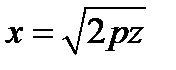Поверхность, полученная при вращении этой линии вокруг оси 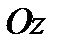, будет задаваться уравнением 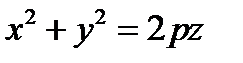или 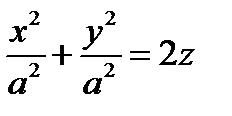– каноническое уравнение параболоида вращения.

О п р е д е л е н и е. Поверхность, полученная из параболоида вращения путем сжатия к плоскости, проходящей через ось вращения, называется эллиптическим параболоидом.

Выполнив сжатие к плоскости , получим каноническое уравнение эллиптического параболоида:

.

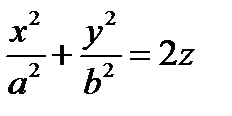Исследование эллиптического параболоида методом сечений:

1. Из уравнения следует, что плоскости являются плоскостями симметрии, а ось 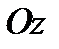– осью симметрии.

2. При пересечении эллиптического параболоида с плоскостью 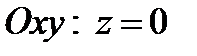получаем точку 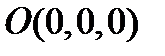– вершина эллиптического параболоида.

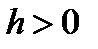3. При пресечении эллиптического параболоида с плоскостью , параллельной плоскости , получаем эллипс ( ) или мнимый эллипс ( ).

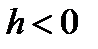4. При пересечении эллиптического параболоида с плоскостью 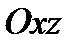или плоскостями ей параллельными ( ), получаем параболы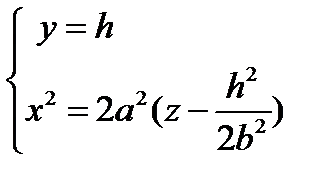

с одним и тем же фокальным параметром 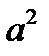. То есть это будут одинаковые параболы, расположенные в параллельных плоскостях.

5. Аналогично, при пересечении эллиптического параболоида с плоскостью 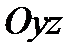и параллельными ей плоскостями, будем получать одинаковые параболы с фокальным параметром .

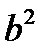Из пунктов 4 и 5 исследования эллиптического параболоида методом сечений следует другой способ получения эллиптического параболоида.

Пусть 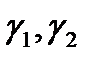– две параболы с общей вершиной, общей осью, расположенные в перпендикулярных плоскостях, и их ветви направлены в одну сторону. Тогда, поверхность, полученная смещением одной параболы параллельно самой себе так, что её вершина скользит по другой параболе, будет эллиптическим параболоидом.

Пусть 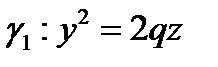– неподвижная парабола, а 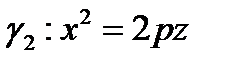– подвижная парабола. Можно показать, что координаты любой точки 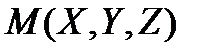поверхности Ф, образованной смещением 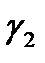параллельно самой себе так, что её вершина скользит по параболе , и только координаты этих точек будут удовлетворять уравнению 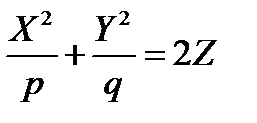. То есть поверхность Ф является эллиптическим параболоидом.

Если 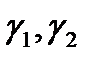– две параболы с общей вершиной, общей осью, расположенные в перпендикулярных плоскостях, и их ветви направлены в противоположные стороны, то уравнение поверхности Ф, полученной смещением одной параболы параллельно самой себе так, что её вершина скользит по другой параболе, будет иметь вид 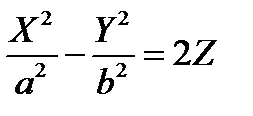или . Поверхность, задаваемая таким уравнением, называется гиперболическим параболоидом (сечения плоскостями, параллельными координатным плоскостям, являются либо гиперболами, либо параболами).